1. チェビシェフの不等式
2014/06/14
@hoxo_m

2. 自己紹介
• hoxo_m
某ECサイトでデータ分析をやっています
• RPubsRecent
RPubs の新着エントリを流す Twitter Bot

3. このお話はフィクションです。

4. • あなたは、とあるメーカー企業の
品質管理部門に勤務する社員です
• ある日、新製品開発に関して話が
あると上司に呼び出されました

5. 上司の部屋で・・・
今、新製品を開発して
いてね
上司
は、はあ・・・
あなた

6. 上司の部屋で・・・
製品評価段階に
来ているんだ
上司
はい・・・
あなた

7. 新製品：petter
• SFじゃない。人によりそうペットロボット
• 製品を一体作るのに 10 万円かかる
• 予算の都合上 10 体をサンプルとする
• 品質評価値
→ 不良品率を出してほしい

8. 上司の部屋で・・・
不良品の出る確率が
3% 以下なら採算が
取れそうなんだ
上司
なるほど・・・
あなた

9. 上司の部屋で・・・
というわけで
品質データから不良品率
を算出してほしい
上司
わかりました
あなた

10. 問題
• 試作品 10 個に対して、それぞれ 0～10 の
品質評価値が算出されている
• この値が 0 か 1 なら不良品と判定する
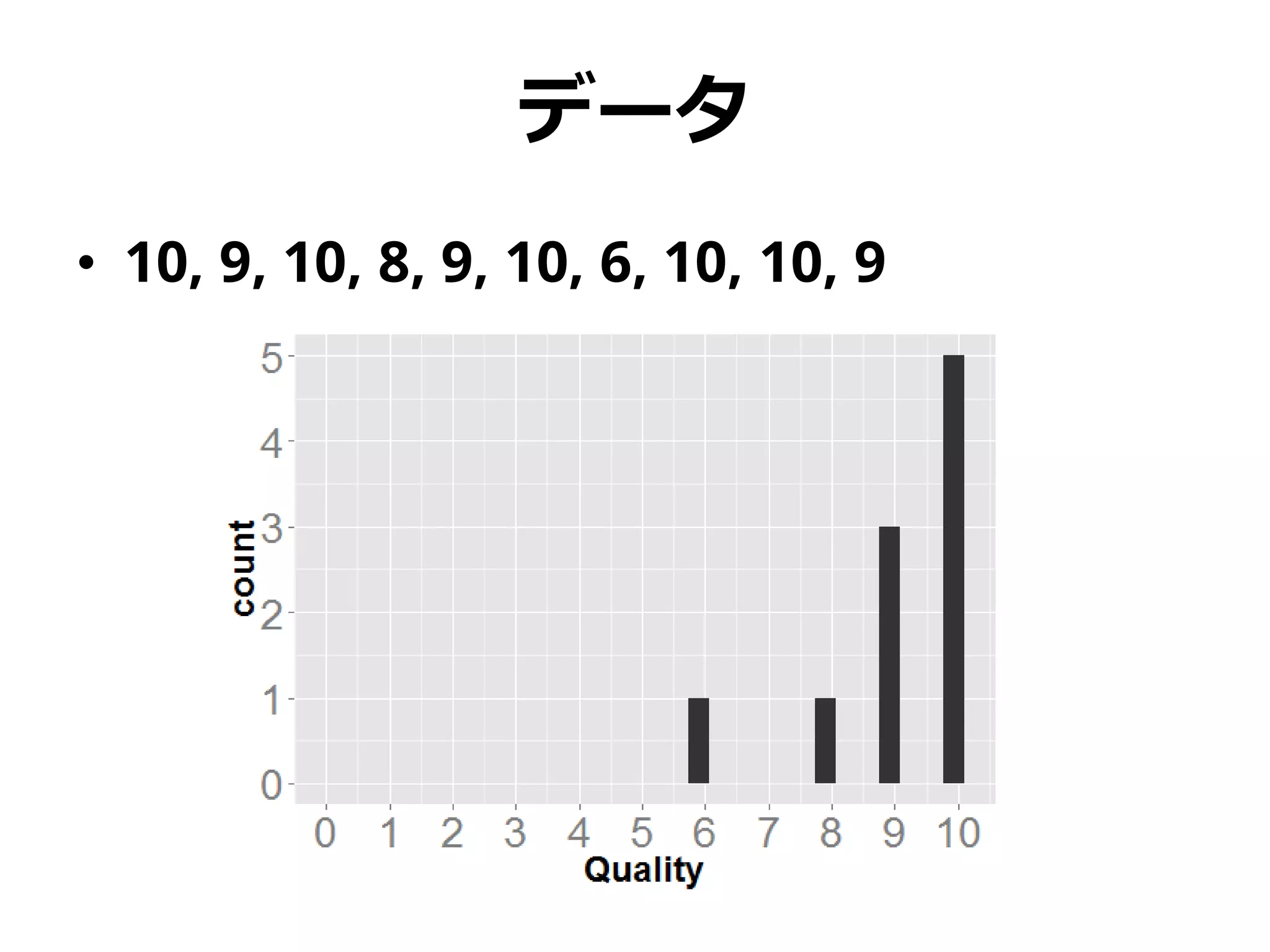
• 実際の評価値：
10, 9, 10, 8, 9, 10, 6, 10, 10, 9
• ここから不良品率を出すことは可能か？

11. データ
• 10, 9, 10, 8, 9, 10, 6, 10, 10, 9

12. 二項分布？
• X = {10, 9, 10, 8, 9, 10, 6, 10, 10, 9}
• 平均値 E[X] = 9.1
• 試行回数 n = 10
• 成功確率 p = E[X]/n = 0.91
• X ~ Binom(10, 0.91) ???

13. コルモゴロフ・スミノフ検定
• 帰無仮説：データが二項分布に従う
data <- c(10, 9, 10, 8, 9, 10, 6, 10, 10, 9)
size = 10
prob <- mean(data) / size
ks.test(data, "pbinom", size=size, prob=prob)
One-sample Kolmogorov-Smirnov test
data: data
D = 0.5, p-value = 0.01348
alternative hypothesis: two-sided
p < 0.05 なので棄却

14. 上司の部屋で・・・
例の件、どうなったかね
上司
どうやら二項分布には
従わないようでして・・
あなた

15. 上司の部屋で・・・
なにを
わけのわからないことを
言っておるんだ！
上司
すみません・・・
もう少し時間を下さい
あなた

16. さて、このあわれな子羊を救う方法は
あるのでしょうか？

17. チェビシェフの不等式
• パフヌーティー・リヴォーヴィッチ・
チェビシェフ(1821–1894)
– ロシアの数学の父
– 弟子：リアプノフ、マルコフ
– チェビシェフの不等式
http://ja.wikipedia.org/wiki/パフヌティ・チェビシェフ
  2
1
k
kXP  

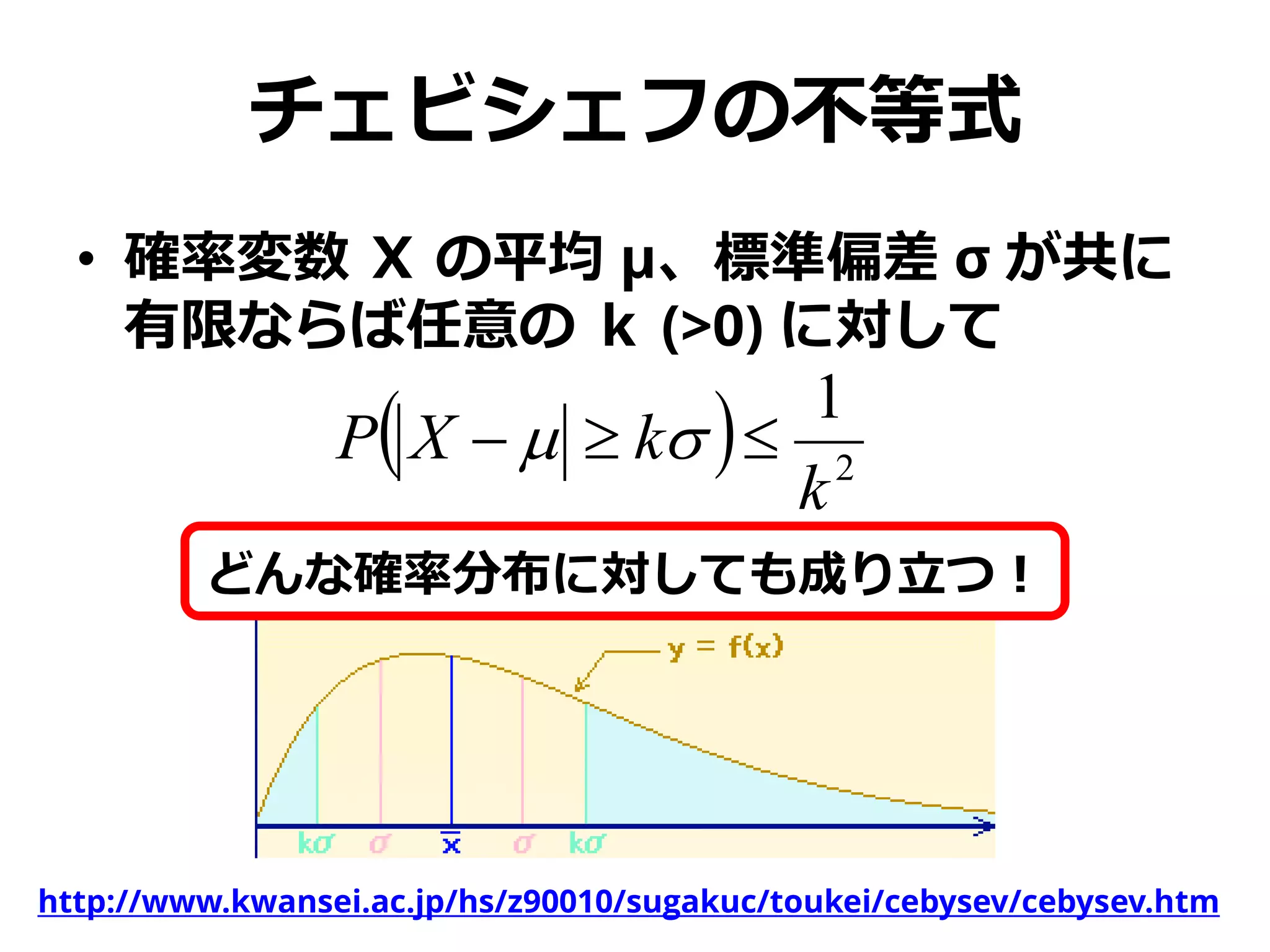
18. チェビシェフの不等式
• 確率変数 Ｘ の平均 μ、標準偏差 σ が共に
有限ならば任意の ｋ (>0) に対して
  2
1
k
kXP  
http://www.kwansei.ac.jp/hs/z90010/sugakuc/toukei/cebysev/cebysev.htm
どんな確率分布に対しても成り立つ！

19. チェビシェフの不等式
• データ： 10, 9, 10, 8, 9, 10, 6, 10, 10, 9
• 平均値： 9.1 標準偏差： 1.29
• 不良品である確率
• チェビシェフの不等式
   1.81.91  XPXP
  2
1
29.11.9
k
kXP 

20. チェビシェフの不等式
• したがって
1.829.1 k   2
1
1
k
XP ならば
3.629.1/1.8 k
025.0
1
2

k
  025.01  XP

21. 上司の部屋で・・・
よくやった！
上司
というわけで
不良品率は 3% 以下で
あると言えます
あなた

22. こうして偉大な統計学者の力によって
あわれな子羊が救われたのであった
完