Recommended
More Related Content
What's hot
What's hot (20)
Similar to ラビットチャレンジレポート 応用数学
Similar to ラビットチャレンジレポート 応用数学 (20)
ラビットチャレンジレポート 応用数学
- 1. 応用数学 ラビット・チャレンジ レポート ALLPPT.com _ Free PowerPoint Templates, Diagrams and Charts
- 5. １．線形代数
- 6. 逆行列をここで理解する目的 最終的には特異値分解の理解を目的としており、特異値分解には逆 行列の理解が必要（目次の順番で理解することで、特異値分解の理解 にたどりつく） 特異値分解を理解しておくと、ある行列が複数の行列の積に分解され、 その行列の要素を落とす（情報量を落とす）といった処理の理解に役 立つ ※ある写真の情報を行列表現したとき、全体感を変えずに情報量落と すイメージ（画像に徐々に濃いモザイクがかかるイメージ、景色が湯気で かすんでいくイメージ） １．１．逆行列（１／２）
- 7. 逆行列 𝐴 を正方行列とし， I を同じ大きさの単位行列とする。 このとき、 𝐴𝐴−1 = 𝐴−1 𝐴= I が成り立つような正方行列𝐴−1が存在するとき，これを𝐴の逆行列と いう。 • 行列的に積が１になるイメージ • 両辺に逆行列をかけることで式変形するようなときに便利 • 例： AB = C ⇒ B = 𝐴−1C ※ 行列の場合はA で割らない １．１．逆行列（２／２）
- 8. 逆行列を持つには 定義の通り正方行列であること 行列式 ≠ 0 ⇔ det (A) ≠ 0 ⇔ |A| ≠ 0 ※以下は2次正方行列の場合 ⇔ 𝑎 𝑏 𝑐 𝑑 とすると a : b ≠ c : d ⇔ ad – bc ≠ 0 ⇔ 𝑣1 = (a b) , 𝑣2 = (c d)のとき 𝑣1, 𝑣2が1次独立 ちなみに逆行列は 1 𝑎𝑑−𝑏𝑐 𝑑 −𝑏 −𝑐 𝑎 １．２．行列式（１／２）
- 9. 逆行列を持つには（続き） 以下は３次正方行列の行列式 𝑎 𝑏 𝑐 𝑑 ⅇ 𝑓 𝑔 ℎ ⅈ とすると以下が ≠ 0 (サラスの公式） a・e・i + b・f・g + d・h・c ←右斜め - c・e・g – f・h・a – b・d・I ←左斜め ちなみに逆行列は、掃き出し法で求める １．２．行列式（２／２）
- 10. 固有値・固有ベクトル 𝐴𝑥 = 𝜆𝑥 となるx (ベクトルの矢印が面倒なので太字）とλが存在 このときxを固有ベクトル、λを固有値と呼ぶ。 なお、Aは正方行列。 x ≠0 意味としては、xを行列Aで変換すると、 xはそのままにλ倍（スカ ラー倍）になるイメージ １．３．固有値分解（１／７）
- 11. 固有値分解 Ax = λx ⇔ 一旦行列表現をして AX = XΛ ⇔ 右からX−1をかけて A = XΛX−1 このように、３つの行列の積に分解できる。 つまり、固有値と固有ベクトルを求めれば、Aを分解できる １．３．固有値分解（２／７）
- 12. 固有値・固有ベクトル導出 1 4 2 3 Ax = λx ⇔ Ax – λx = 0 ⇔ ( A – λI )x = 0 ← Aは行列なので引き算するにはλI ⇔ 定義よりx ≠ 0 である。また、 A – λI が逆行列を持ってしまうと 両辺に左から A – λIの逆行列をかけることで、x = 0 と なってしまうので、これはx ≠ 0 に矛盾するため、 A – λIは逆行列を持たない ⇔ | A – λI | = 0 ← 行列式が0となると逆行列を持たない、だった １．３．固有値分解（３／７）
- 13. 固有値・固有ベクトル導出（続き） 1 4 2 3 ⇔ | 1 4 2 3 – λ 0 0 λ | = 0 ⇔ | 1 − λ 4 2 3 − λ | = 0 ⇔ (1 – λ)(3 – λ) – 8 = 0 ⇔ 3 – λ – 3λ + 𝜆2 - 8 = 0 ⇔ 𝜆2 - 4λ - 5 = 0 ⇔ (λ – 5)(λ + 1) = 0 ∴ λ = 5, -1 １．３．固有値分解（４／７）
- 14. 固有値・固有ベクトル導出（続き） 1 4 2 3 ( A – λI ) x = 0 だったため、これに代入 (1) λ = 5のとき 1 − 5 4 2 3 − 5 𝑥 𝑦 = 0 ⇔ −4 4 2 −2 𝑥 𝑦 = 0 ⇔ 2x – 2y = 0 ⇔ x = y ⇔ x = y = C(Cは任意の定数) とすると、 𝑥 𝑦 = C 1 1 つまり、固有ベクトルの１つは 1 1 ※C=2として 2 2 でもよい １．３．固有値分解（５／７）
- 15. 固有値・固有ベクトル導出（続き） 1 4 2 3 同様に、 (2) λ = -1のとき 2 4 2 4 𝑥 𝑦 = 0 ⇔2x + 4y = 0 ⇔ x =-2 y ⇔ y = C(Cは任意の定数) とすると、 𝑥 𝑦 = C −2 1 つまり、固有ベクトルの１つは −2 1 １．３．固有値分解（６／７）
- 16. 固有値・固有ベクトル導出（最後） 1 4 2 3 A = XΛX−1 だったので A = 1 −2 1 1 5 0 0 −1 1 −2 1 1 −1 ← Xは固有ベクトルを並べたもの = 1 −2 1 1 5 0 0 −1 1/3 2/3 −1/3 1/3 １．３．固有値分解（７／７）
- 18. 特異値・特異ベクトル（続き） 𝐴がm行n列のとき、𝐴𝑇はn行m列。 この積𝐴𝐴𝑇、 𝐴𝑇𝐴はそれぞれ、m行m列、n行n列となる。 つまり、いずれも正方行列。 𝐴v = σu , 𝐴𝑇u = σv 、つまり、 単位ベクトルvを𝐴で変換すると単位ベクトルuのスカラー倍となり、 その単位ベクトルuを𝐴𝑇で変換すると単位ベクトルvのスカラー倍となる u, vが存在する場合、次のことが成り立つ。 （vとuとを𝐴と𝐴𝑇の変換で行ったり来たりするイメージ） １．４．特異値分解（２／１０）
- 19. 特異値・特異ベクトル（続き） 一旦、行列表現をして、 AV = UΣ ※V, Uは直行行列 ⇔ A = UΣ𝑉−1 ⇔ A = UΣ𝑉T ← 直行行列のため 𝑉−1 = 𝑉T ⇔ 𝐴T = (UΣ𝑉T )T = VΣT 𝑈T ← (AB） T = 𝐵T 𝐴T ここで、 𝐴𝐴T = UΣ𝑉TVΣT𝑈T = UΣ ΣT𝑈T ← 𝑉TV = 𝑉−1V = I 𝐴T 𝐴 = VΣT 𝑈T UΣ𝑉T = VΣT Σ𝑉T 𝐴𝐴T = A´と見てみると、A´は正方行列であり 、 固有値・固有ベクトルの式(A´ = VΛ𝑉−1 )と同じ。 固有値・固有ベクトルを求めることができる。（𝐴T 𝐴も同様） １．４．特異値分解（３／１０）
- 20. 特異値・特異ベクトル導出（続き） 1 2 3 3 2 1 𝐴𝐴T = UΣ ΣT𝑈T ⇔ 𝐴𝐴TU = UΣ ΣT ⇔ ( A´ – Σ´)U = 0 ← 一旦 A´ = 𝐴𝐴T, Σ´ = Σ ΣT とみなす ⇔ | 1 2 3 3 2 1 1 3 2 2 3 1 - σ´ 0 0 σ´ | = 0 ⇔ | 14 − σ´ 10 10 14 − σ´ | = 0 ⇔ (14 – σ´)(14 – σ´) – 100 = 0 ⇔ (σ ´ – 24)(λ´ - 4) = 0 ⇔ σ ´ = 4, 24 １．４．特異値分解（４／１０）
- 21. 特異値・特異ベクトル導出（続き） 1 2 3 3 2 1 (1)σ ´ = 24のとき ⇔ 14 − 24 10 10 14 − 24 𝑥 𝑦 = 0 ⇔ -x + y = 0 ⇔ y = C(Cは定数)とすると x = C なので、 𝑥 𝑦 = C 1 1 (2)σ ´ = 4のとき x + y = 0 ⇔ y = Cとするとx = -Cなので、 𝑥 𝑦 = C −1 1 １．４．特異値分解（５／１０）
- 22. 特異値・特異ベクトル導出（続き） 1 2 3 3 2 1 ∴ U = 1/√2 −1/√2 1/√2 1/√2 ← 単位ベクトルのため大きさ１ したがって、A = UΣ𝑉T = 1/√2 −1/√2 1/√2 1/√2 √24 0 0 √4 𝑉T ※ ΣΣT = 𝜎1 0 0 0 𝜎2 0 𝜎1 0 0 𝜎2 0 0 = 𝜎1 2 0 0 𝜎2 2 のため、 固有値は√記号をとって、√24、√4となっている。 なお、𝜎1> 𝜎2 （特異値分解では対角線の左上が大きくなる） １．４．特異値分解（６／１０）
- 23. 特異値・特異ベクトル導出（続き） 1 2 3 3 2 1 A = UΣ𝑉T , 𝐴T = VΣT 𝑈T だったので 𝐴T𝐴= VΣT𝑈TUΣ𝑉T = VΣTΣ𝑉T としてVも同じく求められる 𝐴T 𝐴 = 10 8 6 8 8 8 6 8 10 また、Aは2行3列のため、 A = UΣ𝑉T からUは2行2列、Σは2行3列、 𝑉T は3行3列。し たがって、以下となり３番目の固有値を示す3行3列目が０のため、 3つ目の固有値は 0 となる。 ΣT Σ = 𝜎1 0 0 𝜎2 0 0 𝜎1 0 0 0 𝜎2 0 = 𝜎1 2 0 0 0 𝜎2 2 0 0 0 0 １．４．特異値分解（７／１０）
- 24. 特異値・特異ベクトル導出（続き） 1 2 3 3 2 1 λ = 24, 4, 0でそれぞれ固有ベクトルを求めて V = 1/√3 1/√2 1/√6 1/√3 0 −2/√6 1/√3 −1/√2 1/√6 となるため、 𝑉T = 1/√3 1/√3 1/√3 1/√2 0 −1/√2 1/√6 −2/√6 1/√6 １．４．特異値分解（８／１０）
- 25. 特異値・特異ベクトル導出（続き） 1 2 3 3 2 1 λ = 24, 4, 0でそれぞれ固有ベクトルを求めて V = 1/√3 1/√2 1/√6 1/√3 0 −2/√6 1/√3 −1/√2 1/√6 のため、 𝑉T = 1/√3 1/√3 1/√3 1/√2 0 −1/√2 1/√6 −2/√6 1/√6 １．４．特異値分解（９／１０）
- 26. 特異値・特異ベクトル導出（最後） 1 2 3 3 2 1 A = UΣ𝑉T より A = 1/√2 −1/√2 1/√2 1/√2 √24 0 0 0 √4 0 1/√3 1/√3 1/√3 1/√2 0 −1/√2 1/√6 −2/√6 1/√6 １．４．特異値分解（１０／１０）
- 27. 特異値・特異ベクトル導出（最後） A = 1/√2 −1/√2 1/√2 1/√2 √24 0 0 0 √4 0 1/√3 1/√3 1/√3 1/√2 0 −1/√2 1/√6 −2/√6 1/√6 A = ①×③×⑤ + ②×④×⑥ + ・・・・とすると (1) k = 2 A = ①×③×⑤ + ②×④×⑥ (2) k = 1 A = ①×③×⑤ (3) これにより、元の行列Aの情報を徐々に削減することが可能。 １．５．次元削減 ① ② ③ ④ ⑤ ⑥
- 28. ２．確率・統計
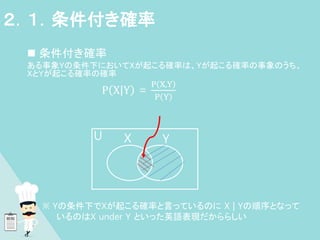
- 30. 条件付き確率 ある事象Yの条件下においてXが起こる確率は、Yが起こる確率の事象のうち、 XとYが起こる確率の確率 P | X Y = P X,Y P Y ※ Yの条件下でXが起こる確率と言っているのに X | Yの順序となって いるのはX under Y といった英語表現だかららしい ２．１．条件付き確率 U X Y
- 31. ベイズの定例 因果関係を逆にできる P | X Y = P X,Y P Y その逆は P | Y X = P X,Y P X でありP(X)を両辺にかけて P | Y X P(X) = P(X,Y) したがって P | X Y = P X,Y P Y = P Y|X P(X) P Y このように、P(X|Y) が P(X), P(Y), P(Y|X)で表すことができる 、 ２．２．ベイズの定例
- 32. 平均と期待値 X = 𝑥𝑖という値が観測される確率を𝑝𝑖、観測される回数を𝑁𝑖、とすると、 平均𝑥は 期待値μは 𝑥 = Σ 𝑥𝑖 𝑁𝑖 𝑁 μ = Σ 𝑥𝑖𝑝𝑖 N → ∞のとき、 𝑁𝑖 𝑁 = 𝑝𝑖 したがって、 𝑥 = μ。確率分布の期待値は母集団の平均値と一致する。 ２．３．期待値／分散／共分散／標準偏差
- 33. 期待値 X = 𝑥𝑖という値が観測される確率を𝑝𝑖、観測される回数を𝑁𝑖、とすると、 平均𝑥は 期待値μは 𝑥 = Σ 𝑥𝑖 𝑁𝑖 𝑁 μ = Σ 𝑥𝑖𝑝𝑖 N → ∞のとき、 𝑁𝑖 𝑁 = 𝑝𝑖 したがって、 𝑥 = μ。確率分布の期待値は母集団の平均値と一致する。 ※確率変数が連続する値の場合は期待値は、 ∫P(x)f(x)dx ２．３．期待値／分散／共分散／標準偏差
- 34. 分散V(X) 一般的な定義より分散を期待値(平均値) E(X)で表す 期待値（平均値）をμとして（μ = E(X)） V(X) = Σ 𝑥𝑖 − μ 2 𝑝𝑖 = Σ(𝑥𝑖 2 𝑝𝑖 − 2μ𝑥𝑖𝑝𝑖 + 𝜇2𝑝𝑖 ) = Σ𝑥𝑖 2 𝑝𝑖 − 2μ × Σ𝑥𝑖𝑝𝑖 + 𝜇2Σ𝑝𝑖) = E(𝑋2) – 2μ E(X) + 𝜇2𝑝𝑖 = E(𝑋2 ) – 2E(X)×E(X) + 𝜇2 = E(𝑋2) – 2{E(X)}2 + {E(X)}2 = E(𝑋2 ) – {E(X)}2 ２．３．期待値／分散／共分散／標準偏差
- 35. 分散V(X) データ各々の期待値からのズレの平均とも考えれる 期待値（平均値）をμとして（μ = E(X)） V(X) = E{ 𝑋 − μ 2 } = E(𝑋2 -2μX + 𝜇2) = E(𝑋2) -2μE(X) + 𝜇2E(1) = E(𝑋2) – 2E(X)E(X) + {E 𝑋 }2 = E(𝑋2) – {E 𝑋 }2 ２．３．期待値／分散／共分散／標準偏差
- 36. 共分散Cov(X, Y) ２つのデータ系列の傾向の違い • 正の値を取れば似た傾向 • 負の値を取れば逆の傾向 • ゼロを取れば関係性に乏しい期待値 Cov(X, Y) = E{(X - μx)(Y − μy)} = E(XY - Xμy- μxY +μxμy) = E(XY) - E(X)μy - μxE(Y) + μxμy = E(XY) – E(X)E(Y) – E(X)E(Y) + E(X)E(Y) = E(XY) − E X E(Y) ２．３．期待値／分散／共分散
- 37. ベルヌーイ試行 コインの裏表のような二面事象 P（X = x) = 𝑝𝑥 1 − 𝑝 1−x x = 0, 1 • 期待値E(X) E(X) = 1・ 𝑝 + 0 (1 – p) = p • 分散V(X) V(X) = Σ 𝑥 − μ 2 p = 1 − μ 2 p + 0 − μ 2 (1 – p) μ = E(X) = pより p - 𝑝3 - 𝑝2 + 𝑝3 = p - 𝑝2 = p(1 – p) ２．４．ベルヌーイ試行／二項分布／カテゴリカル分布／多項分布
- 38. 二項分布 ベルヌーイ試行の多試行版 P（X) = nCk 𝑝𝑘 1 − 𝑝 n−𝑘 • 期待値E(X) １回１回は独立したベルヌーイ試行なので、１回の期待値はp それがn回であるから E(X) = np • 分散V(X) 分散も同様に V(X) = np(1 – p) ２．４．ベルヌーイ試行／二項分布／カテゴリカル分布／多項分布
- 39. カテゴリカル分布 ベルヌーイ試行の多面版（コイン → サイコロ or ジャンケンなど） P（X = x) = 𝑘=1 𝑛 𝑝𝑘 ２．４．ベルヌーイ試行／二項分布／カテゴリカル分布／多項分布
- 40. 多項分布 二項分布を多項に or カテゴリカル分布をn回に。 講義では問われていないようなので割愛。 期待値、分散は二項分布と同様。 ２．４．ベルヌーイ試行／二項分布／カテゴリカル分布／多項分布
- 43. 情報の重要さは、そのレアリティ、確率にあり I(x) = - log P(x) ビット 以降も公式のみの記載になるのでテキスト参照だが、基礎として重要なの で自己情報量については上記に記載。 ３．１．自己情報量