第5回統計・機械学習若手シンポジウム(StatsMLSymposium'20)にて招待講演依頼を受け発表しました。
https://sites.google.com/view/statsmlsymposium20/%E3%83%9B%E3%83%BC%E3%83%A0?authuser=0
そのときの発表動画はこちらです。
https://www.youtube.com/watch?v=ZbVfah9pnb4
アブストラクト:
正則でない統計モデルのベイズ汎化誤差を解析するための数学的基礎(特異学習理論)が構築され,行列分解のベイズ汎化誤差を司る学習係数(実対数閾値)は完全に解明されている.しかしパラメータ空間に制約条件が付いた場合については明らかにされていない.本研究ではパラメータ制約付きモデルの代表として非負値行列分解(NMF)と潜在ディリクレ配分(LDA)を対象とし,それらのベイズ汎化誤差に対する理論解析を実施する.









![2.特異モデルのベイズ汎化誤差解析
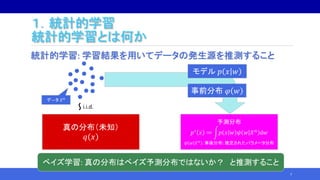
特異学習理論
• 特異学習理論:特異な場合の汎化誤差解析
• 事後分布が正規分布で近似できなくても、汎化誤差の平均値の
挙動が分かる:
𝔼 𝐺 𝑛 =
𝜆
𝑛
−
𝑚 − 1
𝑛 log 𝑛
+ 𝑜
1
𝑛 log 𝑛
.
• 係数𝜆を実対数閾値、 𝑚を多重度という.
‒ KL(q||p)の零点が作る代数多様体から定まる(双有理不変量).
• 自由エネルギー𝐹𝑛も 𝜆, 𝑚 が主要項となる:
𝐹𝑛 = 𝑛𝑆 𝑛 + 𝜆 log 𝑛 − 𝑚 − 1 log log 𝑛 + 𝑂𝑝 1 .
• 正則学習理論は特別な場合として包含される:
𝜆 = 𝑑/2, 𝑚 = 1.
15
[13] Watanabe. 2001](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-12-320.jpg)

![• Def. 下記の複素函数の最大極の絶対値とその位数をそれぞれ
K(w)(とb(w))の実対数閾値と多重度という:
𝜁 𝑧 = 𝐾 𝑤 z 𝑏 𝑤 d𝑤 ,
ここで K(w) と b(w) は非負値(区分的)解析函数である.
• Thm. 𝐾 𝑤 = KL 真||モデル 及び 𝑏 𝑤 = 事前密度とすると,そ
の実対数閾値と多重度は前述の主要項の係数 𝜆 と 𝑚 になる.
17
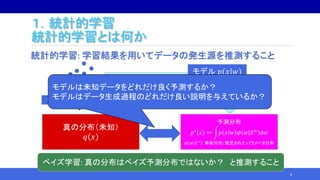
2.特異モデルのベイズ汎化誤差解析
双有理不変量: 実対数閾値
特異学習理論の主結果:
ベイズ汎化誤差がゼータ函数により特徴づけられる!
[7] Watanabe. 2001](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-14-320.jpg)



![2.特異モデルのベイズ汎化誤差解析
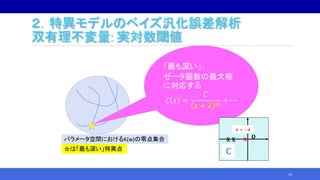
双有理不変量: 実対数閾値
• 実対数閾値𝜆の直感的意味:体積次元
𝜆 = lim
𝑡→+0
log 𝑉 𝑡
log 𝑡
, 𝑉 𝑡 =
𝐾 𝑤 <𝑡
𝜑 𝑤 d𝑤 .
‒ KL(q||p) = 𝐾 𝑤 の零点近傍の体積次元,常に有理数
• 似た概念:ミンコフスキー次元𝑑∗
𝑑∗ = 𝑑 − lim
𝑡→+0
log 𝒱 𝑡
log 𝑡
, 𝒱 𝑡 =
dist 𝑆,𝑤 <𝑡
d𝑤 .
‒ 部分空間 𝑆 ⊂ ℝ 𝑑 のフラクタル次元,無理数になりうる
22
実対数閾値:一般ケースのベイズ汎化誤差 [13]Watanabe. 2001
ミンコフスキー次元:あるクラスのDNNの近似・汎化誤差 [12]Nakada, et. al. 2020
参考1](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-19-320.jpg)
![2.特異モデルのベイズ汎化誤差解析
双有理不変量: 実対数閾値
• 実対数閾値𝜆の直感的意味:体積次元
𝜆 = lim
𝑡→+0
log 𝑉 𝑡
log 𝑡
, 𝑉 𝑡 =
𝐾 𝑤 <𝑡
𝜑 𝑤 d𝑤 .
‒ KL(q||p) = 𝐾 𝑤 の零点近傍の体積次元,常に有理数
• 似た概念:ミンコフスキー次元𝑑∗
𝑑∗ = 𝑑 − lim
𝑡→+0
log 𝒱 𝑡
log 𝑡
, 𝒱 𝑡 =
dist 𝑆,𝑤 <𝑡
d𝑤 .
‒ 部分空間 𝑆 ⊂ ℝ 𝑑 のフラクタル次元,無理数になりうる
23
“Deep Learning is Singular and That’s Good” https://arxiv.org/abs/2010.11560
DNNの理論解析を特異学習理論で行うアプローチと課題
参考2
実対数閾値:一般ケースのベイズ汎化誤差 [13]Watanabe. 2001
ミンコフスキー次元:あるクラスのDNNの近似・汎化誤差 [12]Nakada, et. al. 2020
参考1](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-20-320.jpg)
![2.特異モデルのベイズ汎化誤差解析
双有理不変量: 実対数閾値
• (𝜆, 𝑚) を求める多くの研究がある:
24
特異モデル 文献
混合正規分布 Yamazaki, et. al. in 2003 [15]
縮小ランク回帰=行列分解 Aoyagi, et. al. in 2005 [1]
マルコフモデル Zwiernik in 2011 [16]
非負値行列分解 今日の内容1
潜在ディリクレ配分 今日の内容2
…… ……
本研究の位置づけ:
特異モデルの汎化誤差解析の知識体系への貢献](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-21-320.jpg)
![2.特異モデルのベイズ汎化誤差解析
特異学習理論の応用
• 特異学習理論そのもの:
‒ 広く使える情報量規準 WAIC≒ベイズ汎化損失
(LOOCV並みーー実験的には以上ーーに正確かつ低コスト)
‒ 広く使えるベイズ情報量規準 WBIC≒自由エネルギー
• 実対数閾値の解明:
‒ 特異ベイズ情報量規準 sBIC≒自由エネルギー
(WBICより正確かつ低コスト)
‒ 交換モンテカルロ法の逆温度(交換確率を一定にする)
‒ MCMCによる事後分布の評価
実対数閾値の一致推定量
25
“クリア特典”
By 渡辺澄夫先生
Ref. http://watanabe-
www.math.dis.titech.ac.jp/users/
swatanab/chap45_46.pdf
https://publicdomainq.net/treasure-box-0012726/
[8] Watanabe.
[2] Drton & et al.
[11] Nagata & et al.
[8] Imai.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-22-320.jpg)

![3.パラメータ制約
モチベーション
• パラメータ領域に制約を付けてモデリングすることがしばしばある
‒ 解釈性の良い結果を得るために付けられる
1. 非負値制約
2. 単体制約 ……など
27
Coefficients Coefficients
Non-negative
restriction
Legend
・TVCM
・DM
・Rating
・Reviews
E.g. Logistic regression of purchase existence for a product.
[9] Kohjima. 2016](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-24-320.jpg)
![3.パラメータ制約
モチベーション
data{
int<lower=1> n; //number of sample
int<lower=1> M; //row dimension of input
int<lower=1> H; //hidden dimension
int<lower=1> N; //column dimension of input
int x[M,N,n]; //matrix to be decomposed by A and B
real<lower=0> alpha; //hyperparameter for gamma dist
real<lower=0> beta; //hyperparameter for gamma dist
}
parameters{
matrix<lower=0>[M, H] A; //non-neg constraint
matrix<lower=0>[H, N] B; //non-neg constraint
simplex[M] sA[H]; //simplex constraint
simplex[H] sB[N]; //simplex constraint
}
//modelは略
28
確率的プログラミング言語Stanを用いたパラメータ
制約の記述例:
型として や が表現できるため,
柔軟なモデリングが可能](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-25-320.jpg)
![3.パラメータ制約
モチベーション
data{
int<lower=1> n; //number of sample
int<lower=1> M; //row dimension of input
int<lower=1> H; //hidden dimension
int<lower=1> N; //column dimension of input
int x[M,N,n]; //matrix to be decomposed by A and B
real<lower=0> alpha; //hyperparameter for gamma dist
real<lower=0> beta; //hyperparameter for gamma dist
}
parameters{
matrix<lower=0>[M, H] A; //non-neg constraint
matrix<lower=0>[H, N] B; //non-neg constraint
simplex[M] sA[H]; //simplex constraint
simplex[H] sB[N]; //simplex constraint
}
//modelは略
29
確率的プログラミング言語Stanを用いたパラメータ
制約の記述例:
型として や が表現できるため,
柔軟なモデリングが可能
制約を付けてモデリングすると推定
精度はどうなるのだろうか?](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-26-320.jpg)




![3.パラメータ制約
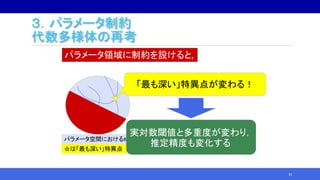
パラメータ制約付きモデルの汎化誤差解析
パラメータ制約付きモデルの代表例として行列分解型の次を解析:
• Non-negative matrix factorization (NMF)
‒ Based on our previous works:
https://doi.org/10.1016/j.neucom.2017.04.068 [3]
https://doi.org/10.1109/ssci.2017.8280811 [4]
https://doi.org/10.1016/j.neunet.2020.03.009 [6]
• Latent Dirichlet allocation (LDA)
‒ Based on our previous/going work:
https://doi.org/10.1007/s42979-020-0071-3 [5]
https://arxiv.org/abs/2008.01304 [7]
35](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-32-320.jpg)





![4.非負値行列分解
問題設定
• 統計モデルとしてのNMF: 複数の行列の分解を扱う
‒ データ: 𝑋 𝑛 = 𝑋 1 , … , 𝑋 𝑛 ; 𝑀 × 𝑁 × 𝑛
各データ行列の(i,j)要素の真の分布 𝑞 𝑋𝑖𝑗 = Poi 𝑋𝑖𝑗| 𝑈0 𝑉0 𝑖𝑗 .
𝑈0; 𝑀 × 𝐻0, 𝑉0; 𝐻0 × 𝑁
‒ モデルを 𝑝 𝑋𝑖𝑗|𝑈, 𝑉 = Poi 𝑋𝑖𝑗| 𝑈𝑉 𝑖𝑗 とし,
事前分布を 𝜑 𝑈, 𝑉 = Gam 𝑈𝑖𝑘|𝜙 𝑈, 𝜃 𝑈 Gam 𝑉𝑘𝑗|𝜙 𝑉, 𝜃 𝑉 とする.
𝑈; 𝑀 × 𝐻, 𝑉; 𝐻 × 𝑁
42
n
X
U
V
𝑃 𝑋, 𝑈, 𝑉 = 𝑃 𝑋 𝑈, 𝑉 𝑃 𝑈 𝑃 𝑉
Poi 𝑥|𝑐 =
𝑐 𝑥
𝑒−𝑐
𝑥!
Gam 𝑎|𝜙, 𝜃 =
𝜃 𝜙
Γ 𝜃
𝑎 𝜙
𝑒−𝜃𝑎
[10] Kohjima. 2017.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-38-320.jpg)
![4.非負値行列分解
問題設定
• 統計モデルとしてのNMF: 複数の行列の分解を扱う
‒ データ: 𝑋 𝑛 = 𝑋 1 , … , 𝑋 𝑛 ; 𝑀 × 𝑁 × 𝑛
各データ行列の(i,j)要素の真の分布 𝑞 𝑋𝑖𝑗 = Poi 𝑋𝑖𝑗| 𝑈0 𝑉0 𝑖𝑗 .
𝑈0; 𝑀 × 𝐻0, 𝑉0; 𝐻0 × 𝑁
‒ モデルを 𝑝 𝑋𝑖𝑗|𝑈, 𝑉 = Poi 𝑋𝑖𝑗| 𝑈𝑉 𝑖𝑗 とし,
事前分布を 𝜑 𝑈, 𝑉 = Gam 𝑈𝑖𝑘|𝜙 𝑈, 𝜃 𝑈 Gam 𝑉𝑘𝑗|𝜙 𝑉, 𝜃 𝑉 とする.
𝑈; 𝑀 × 𝐻, 𝑉; 𝐻 × 𝑁
43
n
X
U
V
𝑃 𝑋, 𝑈, 𝑉 = 𝑃 𝑋 𝑈, 𝑉 𝑃 𝑈 𝑃 𝑉
Poi 𝑥|𝑐 =
𝑐 𝑥
𝑒−𝑐
𝑥!
Gam 𝑎|𝜙, 𝜃 =
𝜃 𝜙
Γ 𝜃
𝑎 𝜙
𝑒−𝜃𝑎
n
X
A
B
n
X
A
B
行列 X を積UV に分解する通常の
NMFを確率モデル化.
𝑿
𝑵 𝑯 𝑵
𝑴
𝑼 𝑽𝑯
[14] Kohjima. 2016
複数の行列の分解が必要な例:
・購買解析
・交通流解析
[10] Kohjima. 2017.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-39-320.jpg)
![4.非負値行列分解
NMFの実対数閾値
• NMFの実対数閾値 𝝀 は以下の不等式を満たす:
𝝀 ≤
𝟏
𝟐
𝑯 − 𝑯 𝟎 𝐦𝐢𝐧 𝑴𝝓 𝑼, 𝑵𝝓 𝑽 + 𝑯 𝟎 𝑴 + 𝑵 − 𝟏 .
等号は 𝑯 = 𝑯 𝟎 = 𝟏 or 𝑯 𝟎 = 𝟎 のとき成立する.
‒ 𝐻0 = 0のときは制約なし行列分解より大きなλとなる.
• 𝝓 𝑼 = 𝝓 𝑽 = 𝟏のとき更にタイトなバウンドが
成立する.
44
[4] H. and Watanabe. 2017.
[3] H. and Watanabe. 2017.
[6] H. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-40-320.jpg)
![4.非負値行列分解
NMFの実対数閾値
• NMFの実対数閾値 𝝀 は以下の不等式を満たす:
𝝀 ≤
𝟏
𝟐
𝑯 − 𝑯 𝟎 𝐦𝐢𝐧 𝑴𝝓 𝑼, 𝑵𝝓 𝑽 + 𝑯 𝟎 𝑴 + 𝑵 − 𝟏 .
等号は 𝑯 = 𝑯 𝟎 = 𝟏 or 𝑯 𝟎 = 𝟎 のとき成立する.
‒ 𝐻0 = 0のときは制約なし行列分解より大きなλとなる.
• 𝝓 𝑼 = 𝝓 𝑽 = 𝟏のとき更にタイトなバウンドが
成立する.
• 主結果と先行研究を合わせるとNMFの
変分近似誤差の下界も得られ,相転移の
違いも確認できる(右図).
45
[6] H. 2020.
[4] H. and Watanabe. 2017.
[3] H. and Watanabe. 2017.
[6] H. 2020.
https://arxiv.org/abs/1809.02963
[10] Kohjima. 2017.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-41-320.jpg)

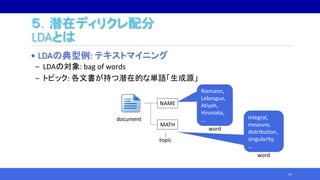
![5.潜在ディリクレ配分
LDAとは
49
FOOD
Alice
sushi
NAME
MATH
Riemann
integral
NAME
・
・
・
・
・
・
FOOD pudding
・
・
・
NAME Lebesgue
LDAによるデータ(単語)の生成過程モデリング
Document 1
Document N
[5] H. and Watanabe. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-45-320.jpg)
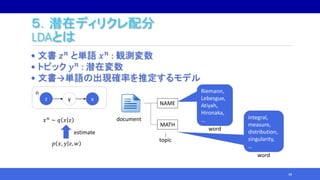
![5.潜在ディリクレ配分
LDAとは
50
FOOD
Alice
sushi
NAME
MATH
Riemann
integral
NAME
・
・
・
・
・
・
FOOD pudding
・
・
・
NAME Lebesgue
LDAによるデータ(単語)の生成過程モデリング
Document 1
Document N
文書jのトピック比率 𝑏𝑗 = 𝑏1𝑗, … , 𝑏 𝐻𝑗
トピックkの単語比率 𝑎 𝑘 = 𝑎1𝑘, … , 𝑎 𝑀𝑘
[5] H. and Watanabe. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-46-320.jpg)




![5.潜在ディリクレ配分
確率行列分解(SMF)
• NMFにおいて非負値行列を確率行列に置き換えてみる.
‒ 各列が単体上にあるという制約→非負値制約より強い
• 置き換えた場合のモデルを確率行列分解(SMF)という.
• LDAとSMFは同じ実対数閾値を持つことが証明できる.
‒ LDAのKL情報量: 𝐾 𝑤 = 𝑧 𝑥 𝑞 𝑥 𝑧 𝑞 𝑧 log
𝑞 𝑥 𝑧
𝑝 𝑥 𝑧, 𝐴, 𝐵
‒ SMFの二乗誤差: 𝐻 𝑤 = 𝐴𝐵 − 𝐴 𝑜 𝐵𝑜
2
‒ ある定数𝑐1, 𝑐2に対して 𝑐1 𝐻 𝑤 ≤ 𝐾 𝑤 ≤ 𝑐2 𝐻 𝑤 の成立を証明できる.
55
[5] H. and Watanabe. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-51-320.jpg)
![5.潜在ディリクレ配分
確率行列分解(SMF)
• NMFにおいて非負値行列を確率行列に置き換えてみる.
‒ 各列が単体上にあるという制約→非負値制約より強い
• 置き換えた場合のモデルを確率行列分解(SMF)という.
• LDAとSMFは同じ実対数閾値を持つことが証明できる.
‒ LDAのKL情報量: 𝐾 𝑤 = 𝑧 𝑥 𝑞 𝑥 𝑧 𝑞 𝑧 log
𝑞 𝑥 𝑧
𝑝 𝑥 𝑧, 𝐴, 𝐵
‒ SMFの二乗誤差: 𝐻 𝑤 = 𝐴𝐵 − 𝐴 𝑜 𝐵𝑜
2
‒ ある定数𝑐1, 𝑐2に対して 𝑐1 𝐻 𝑤 ≤ 𝐾 𝑤 ≤ 𝑐2 𝐻 𝑤 の成立を証明できる.
56
SMFの実対数閾値を求めればよい!
[5] H. and Watanabe. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-52-320.jpg)
![5.潜在ディリクレ配分
LDA~SMFの実対数閾値
【本研究の主結果】
LDAの実対数閾値𝜆を明らかにした:
(1) ①N+H0≦M+H & ②M+H0≦N+H & ③H+H0≦M+Nのとき,
57
𝜆 =
1
8
2 𝐻 + 𝐻0 𝑀 + 𝑁 − 𝑀 − 𝑁 2
− 𝐻 + 𝐻0
2
− 𝛿,
𝛿 =
𝑁
2
, 𝑀 + 𝑁 + 𝐻 + 𝐻0: 偶数.
𝑁
2
−
1
8
, 𝑀 + 𝑁 + 𝐻 + 𝐻0: 奇数.
Thm. 3.1. in https://arxiv.org/abs/2008.01304
[7] H. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-53-320.jpg)
![5.潜在ディリクレ配分
LDA~SMFの実対数閾値
【本研究の主結果】
LDAの実対数閾値𝜆を明らかにした:
(2) not ①, i.e. M+H<N+H0のとき,
58
𝜆 =
1
2
𝑀𝐻 + 𝑁𝐻0 − 𝐻𝐻0 − 𝑁 .
Thm. 3.1. in https://arxiv.org/abs/2008.01304
[7] H. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-54-320.jpg)
![5.潜在ディリクレ配分
LDA~SMFの実対数閾値
【本研究の主結果】
LDAの実対数閾値𝜆を明らかにした:
(3) not ②, i.e. N+H<M+H0のとき,
59
𝜆 =
1
2
𝑁𝐻 + 𝑀𝐻0 − 𝐻𝐻0 − 𝑁 .
Thm. 3.1. in https://arxiv.org/abs/2008.01304
[7] H. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-55-320.jpg)
![5.潜在ディリクレ配分
LDA~SMFの実対数閾値
【本研究の主結果】
LDAの実対数閾値𝜆を明らかにした:
(4) not ③, i.e. M+N<H+H0のとき,
多重度は(1)の奇数ケースで 𝑚 = 2,それ以外で 𝑚 = 1.
60
𝜆 =
1
2
𝑀𝑁 − 𝑁 .
Thm. 3.1. in https://arxiv.org/abs/2008.01304
[7] H. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-56-320.jpg)
![5.潜在ディリクレ配分
LDA~SMFの実対数閾値
• 真を固定してトピック数を増やすとどうなるか?
61
実対数閾値lim
𝑛→∞
𝑛𝔼𝐺𝑛
正則モデルと大きく異なる挙動
• パラメータ次元/2(黄◆):
線型に増加して非有界
• LDAの実対数閾値(青●):
非線形かつ上に有界
𝑑
2
=
𝑀 − 1 𝐻 + 𝐻 − 1 𝑁
2
.
𝑑
2
𝜆
[7] H. 2020.](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-57-320.jpg)
![5.潜在ディリクレ配分
LDA~SMFの実対数閾値
• LDAの実対数閾値=SMFの実対数閾値
• 行列分解との関係
‒ LDAと行列分解の実対数閾値を𝜆 𝐿𝐷𝐴, 𝜆 𝑀𝐹とすると,
𝜆 𝐿𝐷𝐴 𝑀, 𝑁, 𝐻, 𝐻0
= 𝜆 𝑀𝐹 𝑀 − 1, 𝑁 − 1, 𝐻 − 1, 𝐻0 − 1 +
𝑀 − 1
2
… (1)
= 𝜆 𝑀𝐹 𝑀, 𝑁, 𝐻, 𝐻0 −
𝑁
2
… (2)
‒ (1): 主定理の証明は(1)の証明を介する.
‒ (2): (1)と𝜆 𝑀𝐹[1]から計算して導出する.
• LDAの自由度から自明に得られる式ではない
→単体制約がパラメータ空間を変え汎化誤差に影響
62](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-58-320.jpg)


![References
[1] Aoyagi, M & Watanabe, S. Stochastic complexities of reduced rank regression in Bayesian estimation. Neural Netw.
2005;18(7):924–33.
[2] Drton, M & Plummer, M. A Bayesian information criterion for singular models. J R Stat Soc B. 2017;79:323–80 with discussion.
[3] H, N & Watanabe, S. Upper bound of Bayesian generalization error in non-negative matrix factorization. Neurocomputing.
2017;266C(29 November):21–8.
[4] H, N & Watanabe, S. Tighter upper bound of real log canonical threshold of non-negative matrix factorization and its application to
Bayesian inference. In IEEE symposium series on computational intelligence (IEEE SSCI). (2017). (pp. 718–725).
[5] H, N & Watanabe, S. Asymptotic Bayesian generalization error in latent Dirichlet allocation. SN Computer Science. 2020;1(69):1-22.
[6] H, N. Variational approximation error in non-negative matrix factorization. Neural Netw. 2020;126(June):65-75.
[7] H, N. The exact asymptotic form of Bayesian generalization error in latent Dirichlet allocation. https://arxiv.org/abs/2008.01304
[8] Imai, T. Estimating real log canonical threshold. https://arxiv.org/abs/1906.01341
[9] Kohjima M, Matsubayashi T, Sawada H. Multiple data analysis and non-negative matrix/tensor factorization [I]: multiple data
analysis and its advances. IEICE Transaction. 2016:99(6);543-550. In Japanese.
[10] Kohjima M., & Watanabe S. (2017). Phase transition structure of variational bayesian nonnegative matrix factorization. In
International conference on artificial neural networks (ICANN) (2017). (pp. 146–154).
[11] Nagata K, Watanabe S. Asymptotic behavior of exchange ratio in exchange monte carlo method. Neural Netw. 2008;21(7):980–8.
[12] Nakada, R & Imaizumi, M. Adaptive approximation and generalization of deep neural network with Intrinsic dimensionality. JMLR.
2020;21(174):1-38.
[13] Watanabe, S. Algebraic geometrical methods for hierarchical learning machines. Neural Netw. 2001;13(4):1049–60.
[14] Watanabe, S. Mathematical theory of Bayesian statistics. Florida: CR Press. 2018.
[15] Yamazaki, K & Watanabe, S. Singularities in mixture models and upper bounds of stochastic complexity. Neural Netw.
2003;16(7):1029–38.
[16] Zwiernik P. An asymptotic behaviour of the marginal likelihood for general Markov models. J Mach Learn Res.
2011;12(Nov):3283–310.
65](https://image.slidesharecdn.com/nhayashi-invited-201203055943/85/StatsML-2020-61-320.jpg)
