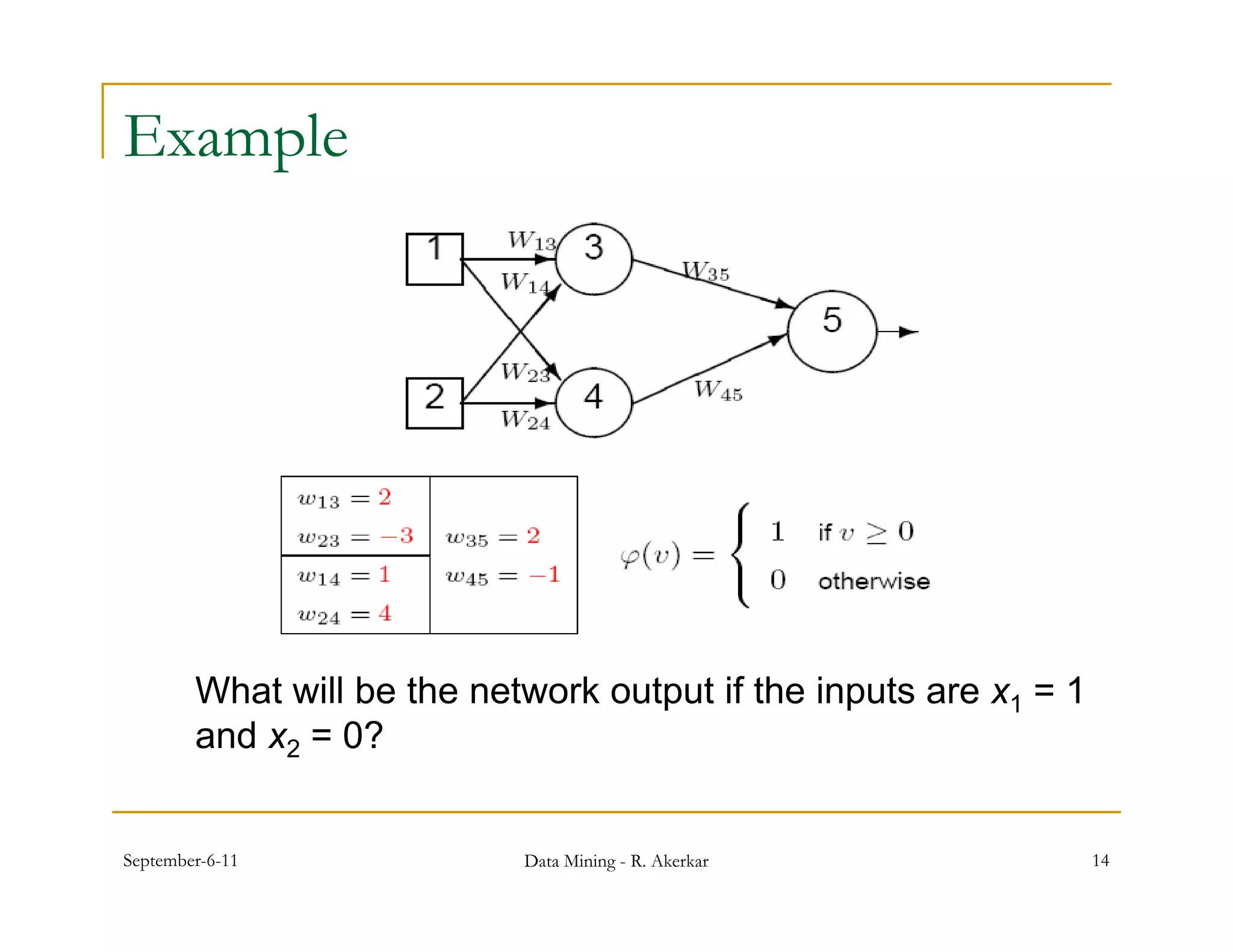
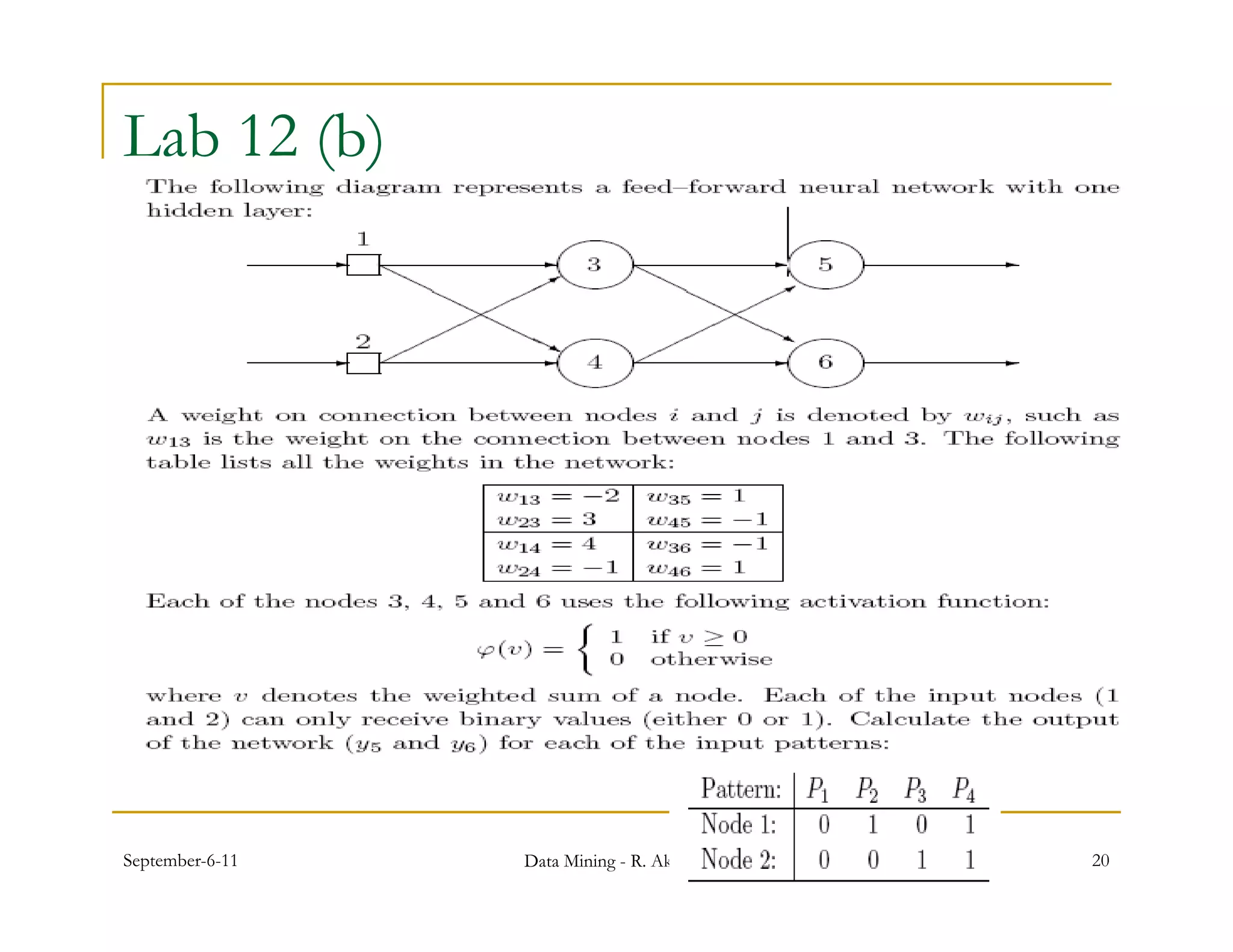
1. Feed-forward neural networks are composed of nodes connected in a directed graph without feedback loops. Information flows from input to output nodes through one or more hidden layers. 2. Each node receives weighted input signals, calculates a weighted sum, and applies an activation function to determine its output. During training, weights are adjusted to minimize error between network outputs and desired targets. 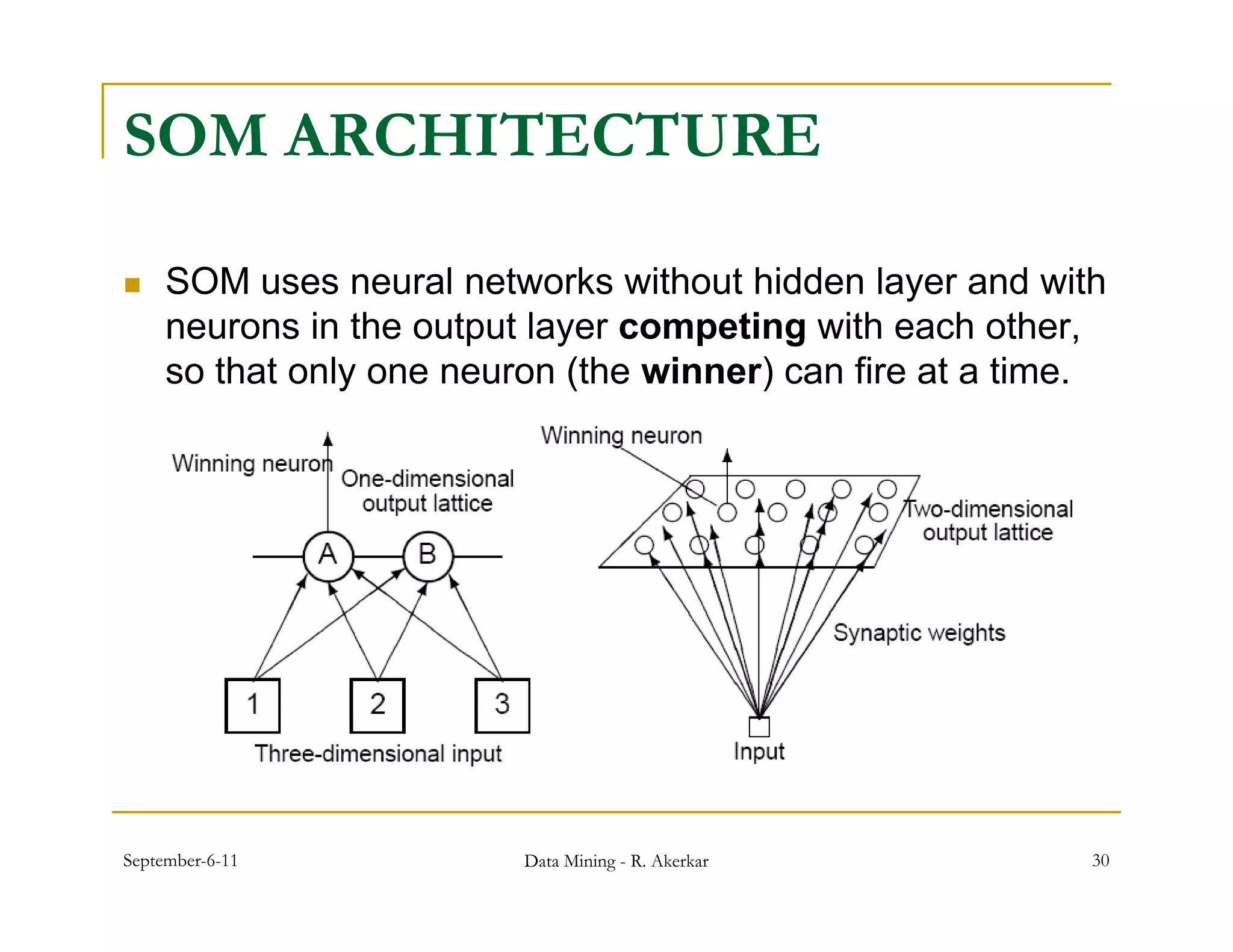3. Self-organizing maps are neural networks that use unsupervised learning to produce a low-dimensional representation of input patterns. They cluster multidimensional data onto a two-dimensional map based on topological similarity.

1. Feed-forward
Feed forward Neural Nets
& Self–Organising Maps
g g p
R. Akerkar
TMRF, Kolhapur, India
September-6-11 Data Mining - R. Akerkar 1

2. Feed–Forward Neural Networks
 HISTORICAL BACKGROUND
 1943 McCulloch and Pitts proposed the first
computational model of a neuron
 1949 H bb proposed th fi t l
Hebb d the first learning rule
i l
 1958 Rosenblatt’s work on perceptrons
 1969 Minsky and Papert’s paper exposed limitations
Papert s
of the theory
 1970s Decade of dormancy for neural networks
 1980–90s Neural network return (self–organisation,
 back–propagation algorithms, etc)
September-6-11 Data Mining - R. Akerkar 2

3. SOME FACTS
 Human brain contains 1011 neurons
 Each neuron is connected 104 others
 Some scientists compared the brain with a
“complex, nonlinear, parallel computer”.
 The l
Th largest modern neural networks achieve
t d l t k hi
the complexity comparable to a nervous
system of a fly
fly.
September-6-11 Data Mining - R. Akerkar 3

4. Neuron
 The main purpose of
neurons is to receive,
analyse and transmit
further th i f
f th the information in
ti i
a form of signals (electric
pulses).
 When neuron sends the
information we say that a
neuron “fires”.
September-6-11 Data Mining - R. Akerkar 4

5. EXCITATION AND INHIBITION
The receptors of a neuron are called synapses, and they are located
on many branches called dendrites. There are many types of
synapses, but roughly they can be divided into two classes:
 Excitatory — a signal received at this synapse “encourages” the
encourages
neuron to fire.
 Inhibitory – a signal received at this synapse will try to make the
neuron “ h t up”.
“shut ”
The neuron analyses all the signals received at its synapses. If most
of them are encouraging, then the neuron gets “excited” and fires its
encouraging excited
own message along a single wire called axon. The axon may have
branches to reach as many other neurons as possible.
September-6-11 Data Mining - R. Akerkar 5

6. A MODEL OF A SINGLE NEURON
(UNIT)
 In 1943 McCulloch and Pitts proposed the following
idea:
 Denote the incoming signals by x = (x1, x2, . . . , xn)
(the input),
 and the output of a neuron by y (the output y = f(x)).
September-6-11 Data Mining - R. Akerkar 6

7. WEIGHTED INPUT
 Synapses (receptors) of a neuron have weights
w = (w1,w2, . . . ,wn) which can have positive
w w ),
(excitatory) or negative (inhibitory) values. Each
incoming signal is multiplied by the weight of the
g g p y g
receiving synapse wixi. Then all the “weighted”
inputs are added together into a weighted sum v:
i=1 wixi = (w, x)
n
 v = w1x 1 + w2x 2 + · · · + wnx n =
 Example Let x = (0, 1, 1) and w = (1,−2, 4). Then
v=1·0−2·1+4·1=2
September-6-11 Data Mining - R. Akerkar 7

8. ACTIVATION (TRANSFER) FUNCTION
 The output of a neuron y is decided by the activation function ϕ
(also transfer function), which uses the weighted sum v as the
argument:t
y = ϕ(v)
 The most popular is a step function ( threshold function):
 If the weighted sum v is large enough (e.g. v = 2 > 0), then the
neuron fires (y = ϕ(2) = 1).
September-6-11 Data Mining - R. Akerkar 8

9. EXAMPLES OF ACTIVATION
FUNCTIONS
September-6-11 Data Mining - R. Akerkar 9

10. FEED–FORWARD NEURAL
NETWORKS
 A collection of neurons connected together in a network can be
represented by a directed graph:
 Nodes and arrows represent neurons and links with the
direction of a signal flow between them. Each node has its
number and a link between two nodes will have a pair of
numbers (e.g. (1, 4) connecting nodes 1 and 4).
 A neural network that does not contain cycles (feedback loops) is
called a feed–forward network (or perceptron).
September-6-11 Data Mining - R. Akerkar 10

11. INPUT AND OUTPUT NODES
 Input nodes receive the signal directly from the environment (nodes
1, 2 and 3). They do not compute anything, but simply transfer the
input values.
 Output nodes send the signal directly to the environment (nodes 4
and 5).
September-6-11 Data Mining - R. Akerkar 11

12. HIDDEN NODES AND LAYERS
 A network may have hidden nodes — they are not connected
directly to the environment (“hidden” inside the network):
 We may organise nodes in layers: input (1,2,3), hidden (4,5) and
output (6,7) layers. Some ff networks can h
t t (6 7) l S t k have several hidd
l hidden
layers.
September-6-11 Data Mining - R. Akerkar 12

13. WEIGHTS
 Each jth node in a network has a set of weights wij . For example,
node 4 h a set of weights w4 = ( 14,w24,w34)
d has f i h (w ).
 A network is defined if we know its topology (its graph), the set of
all weights wij and the transfer functions ϕ of all nodes.
September-6-11 Data Mining - R. Akerkar 13

14. Example
What will be the network output if the inputs are x1 = 1
and x2 = 0?
September-6-11 Data Mining - R. Akerkar 14

15. Answer
 Calculate weighted sums in the first hidden layer:
v3 = w13x1 + w23x2 = 2 · 1 − 3 · 0 = 2
v4 = w14x1 + w24x2 = 1 · 1 + 4 · 0 = 1
 Apply the transfer function:
y3 = ϕ(2) = 1, y4 = ϕ(1) = 1
 Thus, the input to output layer (node 5) is (1, 1).
Now, calculate the weighted sum of node 5:
 v5 = w35y3 + w45y4 = 2 · 1 − 1 · 1 = 1
 The output is y5 = ϕ(1) = 1
September-6-11 Data Mining - R. Akerkar 15

16. TRAINING
Let us inverse the previous problem:
 Suppose th t the inputs to the network are x1 = 1 and x2 = 0 and
S that th i t t th t k d 0, d
ϕ is a step function as in previous example. Find values of
weights wij such that the output of the network y5 = 0.
 This problem is much more difficult, because it has infinite
number of solutions. The process of finding a set of weights such
that for a given input the network produces the desired output is
called training.
 Algorithms for training neural networks can be supervised (with
a “teacher”) and unsupervised (self–organising)
September-6-11 Data Mining - R. Akerkar 16

17. SUPERVISED LEARNING
 A set of pairs of inputs with their corresponding
desired outputs is called a training set. We may
think of a training set as a set of examples.
Supervised learning can be described by the
following
f ll i procedure:d
1. Initially set all the weights to some random values
y g
2. Feed the network with an input from one of the examples in
the training set
3. Compare the output of the network with the desired output
4. Correct the error by adjusting the weights of the nodes
5. Repeat from step 2 with another example from the training
set
September-6-11 Data Mining - R. Akerkar 17

18. Lab 12 (a)
 Consider the unit shown in the figure. Suppose that the weights
corresponding to the three inputs have the following values:
w1 = 2
w2 = -4
W3 = 1
 and the activation of the unit is given by the step function:
 Calculate what will be the output value y of the unit for each of the
p
following input patterns:
September-6-11 Data Mining - R. Akerkar 18

19. Solution 12 (a)
To find the output value y for each p
p pattern we have to:
a) Calculate the weighted sum:
v = i wi xi = w1 x1 + w2 x2 + w3 x3
b) Apply the activation function to v
The calculations for each input pattern are:
September-6-11 Data Mining - R. Akerkar 19

20. Lab 12 (b)
September-6-11 Data Mining - R. Akerkar 20

21. Solution 12 (b)
Continued…
September-6-11 Data Mining - R. Akerkar 21

22. Solution 12 (b)
September-6-11 Data Mining - R. Akerkar 22

23. Self–Organising Maps (SOM)
 HISTORICAL BACKGROUND
 1960s Vector quantisation p
q problems studied byy
mathematicians (Glienn, 1964; Stratonowitch, 1966).
 1973 von der Malsburg did the first computer
simulation demonstrating self–organisation.
 1976 Willshaw and von der Malsburg suggested the
idea of SOM
SOM.
 1980s Kohonen further developed and studied
computational algorithms for SOM
SOM.
September-6-11 Data Mining - R. Akerkar 23

24. EUCLIDEAN SPACE
 Points in Euclidean space have coordinates (e.g. x, y, z) presented
by real numbers R. We denote n–dimensional space by Rn.
 Every point in Rn is defined by n coordinates:
yp y
{x1, . . . , xn}
or by an n–dimensional Vector
x = (x1, . . . , xn)
September-6-11 Data Mining - R. Akerkar 24

25. EXAMPLES
 Example 1 In R1 (one–dimensional space or
(one dimensional
a line) points are represented by just one
number, such as a = (2) or b = (−1).
, ( ) ( )
 Example 2 In R3 (three–dimensional space)
points are represented by three coordinates
x,
x y and z (or x1, x2 and x3) such as
),
a = (2,−1, 3).
September-6-11 Data Mining - R. Akerkar 25

26. EUCLIDEAN DISTANCE
 Distance between two points a = (a1, . . . , an) and b =
p (
(b1, . . . , bn) in Euclidean space Rn is calculated as:
September-6-11 Data Mining - R. Akerkar 26

27. EXAMPLES
September-6-11 Data Mining - R. Akerkar 27

28. MULTIDIMENSIONAL DATA IN
BUSINESS
 A bank gathered information about its customers:
g
 We may consider each entry as a coordinate xi and
all the information about one customer as a point in
Rn (n–dimensional space).
 How to analyse such data?
September-6-11 Data Mining - R. Akerkar 28

29. CLUSTERS
 Multivariate analysis offers variety of methods to analyse
multidimensional data (e.g. NN). SOM is one of such techniques.
One f th
O of the main goals i t fi d clusters of points.
i l is to find l t f i t
 Clusters are groups of points close to each other.
 “Similar” customers would have small Euclidean distance between
them and would belong to the same g p (
g group (cluster).
)
September-6-11 Data Mining - R. Akerkar 29

30. SOM ARCHITECTURE
 SOM uses neural networks without hidden layer and with
y
neurons in the output layer competing with each other,
so that only one neuron (the winner) can fire at a time.
September-6-11 Data Mining - R. Akerkar 30

31. SOM ARCHITECTURE (CONT.)
 Input layer has n nodes. We can represent an input pattern by n–
dimensional vector x = ( 1, . . . , xn) ∈ Rn.
di i l t (x
 Each neuron j on the output layer is connected to all input nodes, so
each neuron has n weights We represent them by n dimensional
weights. n–dimensional
vector wj = (w1j, . . . ,wnj) ∈ R n.
 Usually neurons in the output layer are arranged in a line (
y p y g (one–
dimensional lattice) or in a plane (two–dimensional).
 SOM uses unsupervised learning algorithm, which organises weights
j in h
wj i the output l i so that they “ i i ” the characteristics of the
lattice h h “mimic” h h i i f h
input patterns.
September-6-11 Data Mining - R. Akerkar 31

32. HOW DOES AN SOM WORK
 The algorithm consists of three p
g processes: competition,
p ,
cooperation and adaptation.
 Competition Input pattern x = (x1, . . . , xn) is compared
with th weight vector wj = ( 1j, . . . ,wnj) of every neuron
ith the i ht t (w f
in the output layer. The winner is the neuron whose
weight wj is the closest to the input x in terms of
Euclidean distance:
September-6-11 Data Mining - R. Akerkar 32

33. Example
 Consider SOM with three inputs and two output nodes (A
and B) Let wA = (2 1 3) and wB = ( 2 0 1)
d B). L t (2,−1, d (−2, 0, 1).
 Find which node wins if the input
x = (1 −2 2)
(1, 2,
 Solution:
(−1 −2
What if x = (−1,−2, 0)?
September-6-11 Data Mining - R. Akerkar 33

34. Cooperation
 The winner helps its neighbours in the output lattice.
 Those nodes which are closer to the winner in the lattice get more
help, those which are further away get less.
 If the winner is node i, then the amount of help to node j is
calculated using the neighbourhood function hij(dij), where dij is the
distance between i and j in the lattice. A good example of hij(d) is
g p ( )
Gaussian function:
 Note that the winner also helps itself more than others (for dii = 0).
September-6-11 Data Mining - R. Akerkar 34

35. Adaptation
 After the input x has been presented to SOM, the weights wj of
the nodes are adjusted so that they become “closer” to the input.
The exact formula for adaptation of weights is:
w’j = wj + αhij [x − wj ] ,
where α is the learning rate coefficient.
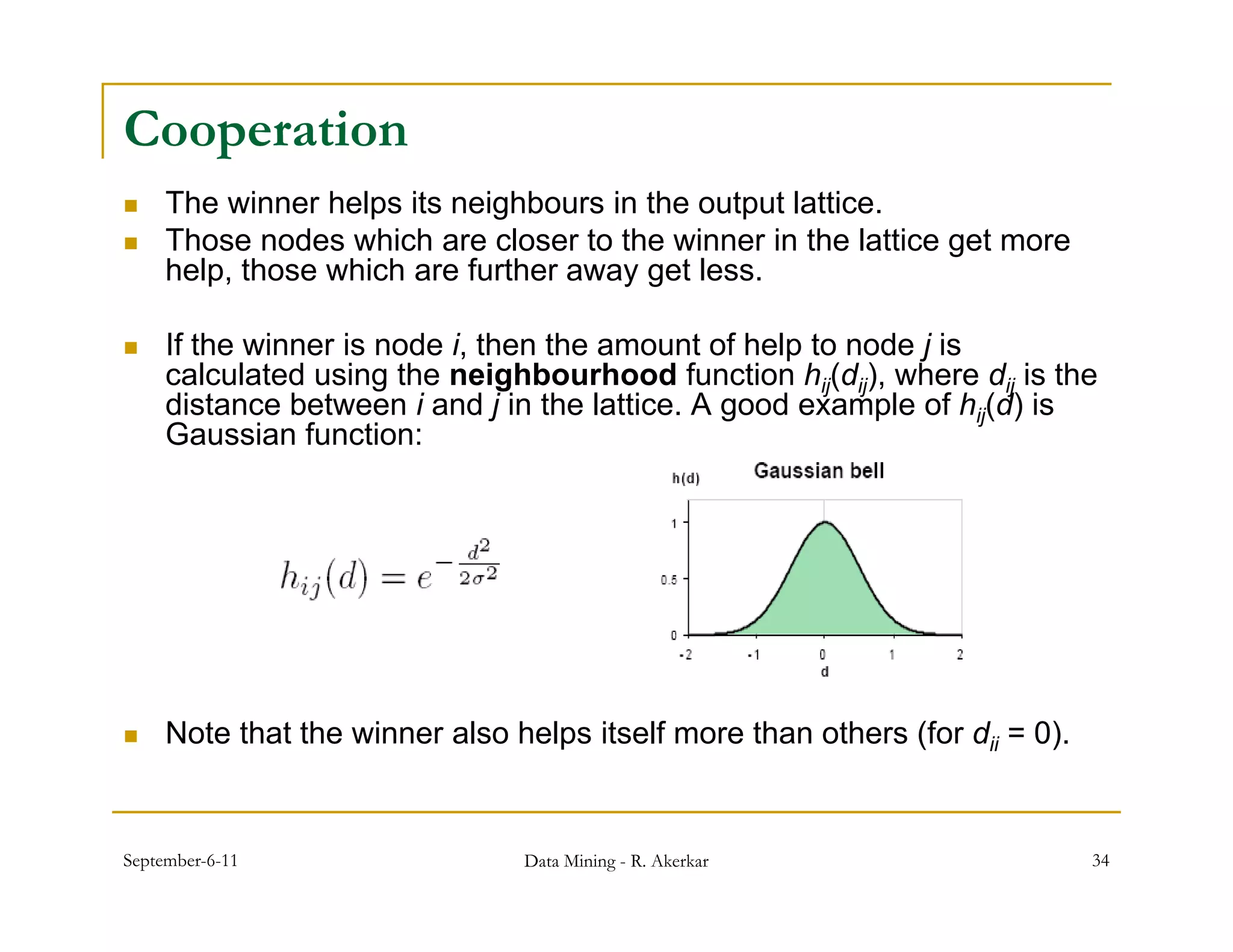
 One can see that the amount of change depends on the
neighbourhood hij of the winner. So, the winner helps itself and
its neighbours to adapt.
 Finally, the neighbourhood hij is also a function of time, such that
the neighbourhood shrinks with time (e.g. σ decreases with t).
September-6-11 Data Mining - R. Akerkar 35

36. Example
 Let us adapt the winning node from earlier Example
(w
( A = (2 1 3) f x = (1 2 2))
(2,−1, for (1,−2,
if α = 0.5 and h = 1:
September-6-11 Data Mining - R. Akerkar 36

37. TRAINING PROCEDURE
1.
1 Initially set all the weights to some random
values
2.
2 Feed a set of data into the network
3. Find the winner
4. Adjust the
4 Adj t th weight of th winner and it
i ht f the i d its
neighbours to be more like the input
5. Repeat f
5 R t from step 2 until th network
t til the t k
stabilises
September-6-11 Data Mining - R. Akerkar 37

38. APPLICATIONS OF SOM IN
BUSINESS
 SOM can be very useful during the intelligence
y g g
phase of decision making. It helps to analyse and
understand rather complex and large amounts of
information (data)
(data).
 Ability to visualise multi–dimensional data can be
used for presentations and reports.
 Identifying clusters in the data (e.g. typical groups of
customers) can help optimise distribution of
resources (e g advertising products selection etc)
(e.g. advertising, selection, etc).
 Can be used to identify credit–card fraud, errors in
data, etc.
September-6-11 Data Mining - R. Akerkar 38

39. USEFUL PROPERTIES OF SOM
 Reducing dimensions (Indeed, SOM is a map
(Indeed
f : Rn → Zm)
 Visualisation of clusters
 Ordered display
 Handles i i data
H dl missing d t
 The learning algorithm is unsupervised.
September-6-11 Data Mining - R. Akerkar 39

40. Similarities and differences between feed-forward
neural networks and self-organising maps
l k d lf ii
Similarities are:
 Both are feed-forward networks (no loops).
 Nodes have weights corresponding to each
link.
 Both networks require training.
September-6-11 Data Mining - R. Akerkar 40

41. The main differences are:
 Self-organising maps (SOM) use just a single output layer, they do not have hidden
layers.
 In feed-forward neural networks (FFNN) we have to calculate weighted sums of the
( ) g
nodes. There are no such calculations in SOM, weights are only compared with the
input patterns using Euclidean distance.
 In FFNN the output values of nodes are important, and they are defined by the
p p , y y
activation functions. In SOM nodes do not have any activation functions, and the
output values are not important.
 In FFNN all the output nodes can re, while in SOM only one.
p , y
 The output of FFNN can be a complex pattern consisting of the values of all the
output nodes. In SOM we only need to know which of the output nodes is the
winner.
 Training of FFNN usually employs supervised learning algorithms, which require a
training set. SOM use unsupervised learning algorithm.
 There are, however, unsupervised training methods for FFNN as well.
September-6-11 Data Mining - R. Akerkar 41

42. Lab 13 (a)
 Consider the self-organising map:
 The output layer of this map consists of six nodes, A, B, C, D, E and F,
which are organised into a two-dimensional lattice with neighbours
connected by lines.
 Each f the t t d h two inputs x1 and x2 ( t shown on the
E h of th output nodes has t i t d (not h th
diagram). Thus, each node has two weights corresponding to these inputs:
w1 and w2. The values of the weights for all output in the SOM nodes are
g
given in the table below:
Calculate which of the six output nodes is the winner if the input pattern is
p p p
x = (2, -4)?
September-6-11 Data Mining - R. Akerkar 42

43. Solution 13 (a)
 First, we calculate the distance for each node:
,
The winner is the node with the smallest distance from x. Thus,
in this case the winner is node C (because 5 is the smallest
distance here).
September-6-11 Data Mining - R. Akerkar 43

44. Lab 13 (b)
September-6-11 Data Mining - R. Akerkar 44

45. Solution 13 (b)
September-6-11 Data Mining - R. Akerkar 45