This document discusses support vector machines (SVMs) for pattern classification. It begins with an introduction to SVMs, noting that they construct a hyperplane to maximize the margin of separation between positive and negative examples. It then covers finding the optimal hyperplane for linearly separable and nonseparable patterns, including allowing some errors in classification. The document discusses solving the optimization problem using quadratic programming and Lagrange multipliers. It also introduces the kernel trick for applying SVMs to non-linear decision boundaries using a kernel function to map data to a higher-dimensional feature space. Examples are provided of applying SVMs to the XOR problem and computer experiments classifying a double moon dataset.

1. CHAPTER 06
SUPPORT VECTOR MACHINES
CSC445: Neural Networks
Prof. Dr. Mostafa Gadal-Haqq M. Mostafa
Computer Science Department
Faculty of Computer & Information Sciences
AIN SHAMS UNIVERSITY
(some of the figures in this presentation are copyrighted to Pearson Education, Inc.)

2. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
 Introduction
 Optimal Hyperplane for Linearly Separable Pattern
 Quadratic Optimization for Finding the Optimal Hyperplan
 Optimal Hyperplane for Nonseparable Patterns
 Underlying Philosophy of SVM for Pattern Calssification
 SVM viewed as Kernel Machine
 The XOR problem
 Computer Experiment
2
Outlines

3. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 3
Introduction
 The main idea of the SVMs may be summed up as
follows:
 “Given a training samples, the SVM constructs a
hyperplane as decision surface in such a way the
margin of separation between positive and negative
examples is maximized.”

4. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 4
Linearly Separable Patterns
 SVM is a binary learning machine.
 Binary classification is the task of separating classes in
feature space.
wTx + b = 0
wTx + b < 0
wTx + b > 0
bxwxg T


)(

5. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq 5
Linearly Separable Patterns
 Which of the linear separators is optimal?

6. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Optimal Decision Boundary
 The optimal decision boundary is the one that
maximize the margin 
6
r
ρ

7. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The Margin 
7
|||| w
w
rxx P 




8. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The Margin 
||||)(then
,0since
||||
)()(
||||
,)(
wrxg
bxw
w
w
w
rbxwxg
w
w
rxxbxwxg
P
T
T
P
T
P
T













8

9. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The Margin 










1
||||
1
1
||||
1
||||
)(
11)(
dif
w
dif
w
w
xg
r
dforbxwxg T





9
r
ρ
1bxwT 
1 bxwT 
0 bxwT 
||||
2
2
w
r 
Then the margin is given as:

10. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Optimal Decision Boundary
 Let {x1, ..., xn} be our data set and let di  {1,-1} be the
class label of xi
 The decision boundary should classify all points
correctly.
 That is, we have a constrained optimization problem
Maximize  = 𝟐𝒓 =
𝟐
𝒘
, or Minimize 𝒘
Subject to 𝒅𝒊(𝒘 𝑻 𝒙 ± 𝒃) ≥ 𝟏
10

11. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The Optimization Problem
 Introduce Lagrange multipliers ,
 That is, the Lagrange function:
Is to be minimized with respect to w and b, i.e,
𝜕𝑱(𝒘,𝒃,)
𝜕𝒘
= 𝟎 ; and
𝜕𝑱(𝒘,𝒃, )
𝜕𝒃
= 𝟎
)1][(||||
2
1
),,(
1
2
 
bxwdwbwJ i
T
i
N
i
i
11

12. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Solving the Optimization Problem
 Need to optimize a quadratic function subject to linear
constraints.
 The solution involves constructing a dual problem where a
Lagrange multiplier αi is associated with every constraint in the
primary problem:
Find 𝛼1…𝛼 𝑁such that
𝑸 𝜶 = 𝛼𝑖 −
1
2
𝛼𝑖 𝛼𝑗 𝑑𝑖 𝑑𝑗x 𝑖x𝑗𝑗𝑖
𝑵
𝒊=𝟏
is maximized and
(1) 𝛼𝑖 𝑑𝑖𝑗
(2) 𝛼1 ≥ 0 ∀ 𝑖
12

13. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The Optimization Problem
 The solution has the form:
and such that 𝒊 ≠ 𝟎
 Each non-zero αi indicates that corresponding xi is a support vector.
 Then the classifying function will have the form:
 Notice that it relies on an inner product between the test point x and the
support vectors xi
 Also keep in mind that solving the optimization problem involved computing
the inner products xi
Txj between all training points!
13
ii
N
i
i xd

1
w  iii
N
i
idb xx1
1

 
bdxg iii
N
i
i  
xx)(
1


14. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
6=1.4
The Optimization Problem
 Support vectors are samples that have non-zero 
Class 1
Class 2
1=0.8
2=0
3=0
4=0
5=0
7=0
8=0.6
9=0
10=0

15. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Optimal Hyperplane for Nonseparable Patterns
Figure 6.3 Soft margin hyperplane (a) Data point xi (belonging to class C1,
represented by a small square) falls inside the region of separation, but on the
correct side of the decision surface. (b) Data point xi (belonging to class C2,
represented by a small circle) falls on the wrong side of the decision surface.
15

16. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Optimal Hyperplane for Nonseparable Patterns
 We allow “error” xi in classification
16
ξi
ξi

17. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Soft Margin Hyperplane
 The old formulation:
 The new formulation incorporating relaxed variables:
Parameter C can be viewed as a way to control overfitting.
17
Find w and b such that
∅ 𝑾 =
𝟏
𝟐
𝑾 𝑻
𝑾 is minimized and for all {(xi ,yi)}
Subject to: 𝒅𝒊(𝒘 𝑻
𝒙 ± 𝒃) ≥ 𝟏
Find w and b such that
∅ 𝐖 =
𝟏
𝟐
𝐖 𝐓 𝐖 + 𝐜 𝝃𝒊𝒊 is minimized for all {(xi ,yi)}
Subject to: 𝒅𝒊(𝒘 𝑻 𝒙 ± 𝒃) ≥ 𝟏 , and ξi ≥ 0 for all i

18. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Soft Margin Hyperplane
 Again, xi with non-zero αi will be support vectors.
 Solution to the dual problem is:
𝑾 = 𝜶𝒊 𝒅𝒊 𝒙𝒊𝒊
and
𝒃 = 𝒅𝒊 𝟏 − 𝝃𝒊 − 𝑾 𝑻
𝒙𝒊
18

19. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Extension to Non-linear Decision Boundary
 Key idea: transform xi to a higher dimensional space
 Input space: the space of xi
 Feature space: the “kernel” space of f(xi)
19
f( )
f( )
f( )
f( )f( )
f( )
f( )
f( )
f(.)
f( )
f( )
f( )
f( )
f( )
f( )
f( )
f( )
f( )
f( )
Feature spaceInput space

20. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Kernel Trick
 The linear classifier relies on inner product between
vectors:
𝑲 𝐱 𝒊, 𝐱 𝒋 = 𝐱𝒊
𝑻 𝐱 𝒋
If every datapoint is mapped into high-dimensional space
via some transformation Φ: x → φ(x), the inner product
becomes:
𝑲 𝐱 𝒊, 𝐱 𝒋 = 𝛟 𝐱𝐢
𝑻 𝛟(𝐱 𝒋)
 A kernel function is some function that corresponds to
an inner product into some feature space.
 K (x, xj) needs to satisfy a technical condition (Mercer
condition) in order for f(.) to exist
20

21. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Mercer’s Theorem
 𝑲 = 𝒌(𝒙𝒊, 𝒙𝒋) ∀𝒊, 𝒋 has to be non-negative definite or
positive semidefinite , that is, it satisfies:
𝒂 𝑻K𝒂 ≥ 𝟎
 Some of kernel functions that satisfy Mercer’s condition:
21

22. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The SVM viewed as Kernel Machine
Figure 6.5 Architecture of support vector machine, using a
radial-basis function network.
22

23. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
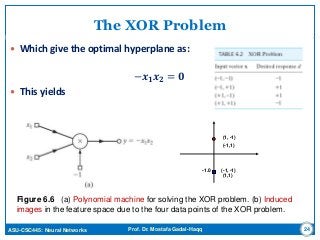
The XOR Problem
 For the two dimensional vectors x=[x1 x2];
 Define the following Kernel:
𝒌 x,x𝒊 = 𝟏 + x 𝑻
x𝒊
2
 Need to show that
K(xi,xj)= φ(xi)Tφ(xj)
K(xi,xj)=(1 + xi
Txj)2
= 1+ xi1
2xj1
2 + 2 xi1xj1 xi2xj2+ xi2
2xj2
2 + 2xi1xj1 + 2xi2xj2=
= [1 xi1
2 √2 xi1xi2 xi2
2 √2xi1 √2xi2]T [1 xj1
2 √2 xj1xj2 xj2
2 √2xj1 √2xj2]
= φ(xi)Tφ(xj),
where
φ(x) = [1 x1
2 √2 x1x2 x2
2 √2x1 √2x2]
23

24. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
The XOR Problem
 Which give the optimal hyperplane as:
−𝒙 𝟏 𝒙 𝟐 = 𝟎
 This yields
Figure 6.6 (a) Polynomial machine for solving the XOR problem. (b) Induced
images in the feature space due to the four data points of the XOR problem.
24
(1, -1)
(-1,1)
(-1, -1)
(1,1)
-1.0

25. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Conclusion
 SVM is a useful alternative to neural networks
 Two key concepts of SVM: maximize the margin
and the kernel trick
 Many active research is taking place on areas
related to SVM
 Many SVM implementations are available on the
web for you to try on your data set!
25

26. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Computer Experiment
Figure 6.7 Experiment on SVM for the double-moon of Fig. 1.8 with
distance d = –6.
26

27. ASU-CSC445: Neural Networks Prof. Dr. Mostafa Gadal-Haqq
Computer Experiment
Figure 6.8 Experiment on SVM for the double-moon of Fig. 1.8 with
distance d = –6.5.
27

28. Principal Component
Analysis (PCA)
Next Time
28