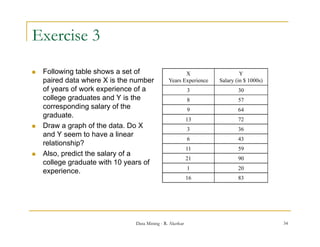
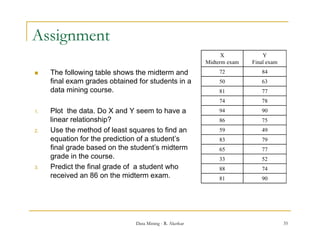
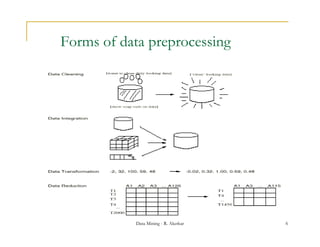
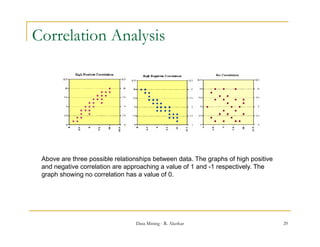
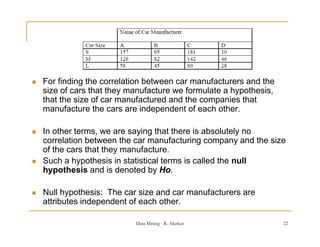
This document discusses data preprocessing techniques for data mining. It explains that real-world data is often dirty, containing issues like missing values, noise, and inconsistencies. Major tasks in data preprocessing include data cleaning, integration, transformation, reduction, and discretization. Data cleaning techniques are especially important and involve filling in missing values, identifying and handling outliers, resolving inconsistencies, and reducing redundancy from data integration. Other techniques discussed include binning data for smoothing noisy values and handling missing data through various imputation methods.

1. Statistics & Data Mining
R. Akerkar
TMRF, Kolhapur, India
Data Mining - R. Akerkar 1

2. Why Data Preprocessing?
 Data in the real world is dirty
y
 incomplete: lacking attribute values, lacking certain
attributes of interest, or containing only aggregate data
 e.g., occupation=
e g occupation=“”
 noisy: containing errors or outliers
 e.g., Salary=“-10”
 inconsistent: containing discrepancies in codes or names
 e.g., Age=“42” Birthday=“03/07/1997”
 e.g., Was rating “1,2,3”, now rating “A, B, C
1,2,3 , A, C”
 e.g., discrepancy between duplicate records
 This is the
Thi i th real world…
l ld
Data Mining - R. Akerkar 2

3. Why Is Data Dirty?
y y
 Incomplete data comes from
 n/a data value when collected
/
 different consideration between the time when the data was
collected and when it is analyzed.
 human/hardware/software problems
 Noisy data comes from the process of data
 Collection instrument’s f lt
C ll ti i t t’ fault
 Data entry
 transmission
 Inconsistent data comes from
 Different data sources
 Functional d
F ti l dependency violation
d i l ti
Data Mining - R. Akerkar 3

4. Why Is Data Preprocessing
Important?
 No quality data no quality mining results!
data,
 Quality decisions must be based on quality data
 e.g., duplicate or missing data may cause incorrect or even
g, p g y
misleading statistics.
 Data warehouse needs consistent integration of quality data
 Data extraction, cleaning, and transformation
comprises the majority of the work of building a data
warehouse. Bill
warehouse —Bill Inmon
Data Mining - R. Akerkar 4

5. Major Tasks in Data Preprocessing
 Data cleaning
 Fill in missing values, smooth noisy data, and resolve
inconsistencies
 Data integration
 Integration of multiple databases, data cubes, or files
 Data transformation
 Normalization and aggregation ( a distance based mining algorithms
provide better results if data is normalized and scaled to range.)
 Data reduction
 Obtains reduced representation in volume but p
p produces the same or
similar analytical results (correlation analysis).
 Data discretization
 Part of data reduction but with particular importance, especially for
p p p y
numerical data.
Data Mining - R. Akerkar 5

6. Forms of data preprocessing
Data Mining - R. Akerkar 6

7. Data Cleaning
g
 Importance
 “Data l
“D t cleaning i one of th th
i is f the three bi
biggest problems i
t bl in
data warehousing”—Ralph Kimball
 “Data cleaning is the number one problem in data
warehousing”—DCI survey
h i ” DCI
 Data cleaning tasks
 Fill in missing values (time consuming)
 Identify outliers and smooth out noisy data
 Correct inconsistent data
 Resolve redundancy caused by data integration
y y g
Data Mining - R. Akerkar 7

8. Missing Data
g
 Data is not always available
 E.g.,
E g many tuples have no recorded value for several attributes
attributes,
such as customer income in sales data
 Missing data may be due to
 equipment malfunction
 inconsistent with other recorded data and thus deleted
 data not entered due to misunderstanding
 certain data may not be considered important at the time of
entry
 not register history or changes of the data
 Missing data may need to be inferred.
Data Mining - R. Akerkar 8

9. How to Handle Missing
Data?
 Ignore the tuple: usually done when class label is missing (assuming the
tasks in classification—not effective when the percentage of missing values
per attribute varies considerably.
 Fill in the missing value manually: t di
i th i i l ll tedious + i f
infeasible?
ibl ?
 Fill in it automatically with
 a global constant : e g “unknown”, a new class?!
e.g., unknown
 the attribute mean
 the attribute mean for all samples belonging to the same class: smarter
 the most probable value: inference-based such as Bayesian formula or
decision tree or regression.
Data Mining - R. Akerkar 9

10. Noisy Data
 Noise: random error or variance in a measured variable.
 For example, for a numeric attribute “price” how can we smooth out
the data to remove the noise.
 Incorrect attribute values may due to
 faulty data collection instruments
 data entry problems
 data transmission problems
 technology limitation
gy
 inconsistency in naming convention
Data Mining - R. Akerkar 10

11. How to Handle Noisy Data?
 Binning method:
 first sort data and partition into (equi-depth) bins
 then one can smooth by bin means, smooth by bin median,
smooth by bin boundaries etc
boundaries, etc.
 Regression
g
 smooth by fitting the data into regression functions
Data Mining - R. Akerkar 11

12. Binning Methods for Data Smoothing
* Binning methods smooth a sorted data by consulting its
neighborhood. Then sorted values are distributed in number of
buckets.
* Sorted data for price (in dollars): 4, 8, 9, 15, 21, 21, 24, 25, 26, 28,
29, 34
* Partition into (equi-depth) bins of depth 4:
- Bin 1: 4, 8, 9, 15
- Bin 2: 21, 21, 24, 25
- Bin 3: 26, 28, 29, 34
* Smoothing by bin means:
- Bin 1: 9, 9, 9, 9
- Bin 2: 23, 23, 23, 23
- Bin 3: 29, 29, 29, 29
* S
Smoothing by bin boundaries:
thi b bi b d i
- Bin 1: 4, 4, 4, 15 Similarly, smoothing
- Bin 2: 21, 21, 25, 25 by bin median can
- Bin 3: 26, 26, 26, 34
, , , be employed.
Data Mining - R. Akerkar 12

13. Simple Discretization Methods: Binning
 Equal-width (distance) partitioning:
 Divides the
Di id th range i t N i t
into intervals of equal size:
l f l i
uniform grid
 if A and B are the lowest and highest values of the
g
attribute, the width of intervals will be: W = (B –A)/N.
 The most straightforward, but outliers may dominate
presentation
 Skewed data is not handled well.
 Binning is
Bi i i applied t each i di id l f t
li d to h individual feature (
(or
attribute). It does not use the class information.
Data Mining - R. Akerkar 13

14.  Equal depth
Equal-depth (frequency) partitioning:
 Divides the range into N intervals, each containing
approximately same number of samples
 Good data scaling
 Managing categorical attributes can be tricky.
Data Mining - R. Akerkar 14

15. Exercise 1
 Suppose the data for analysis includes the attribute Age. The age
values for the data tuples (instances) are (in increasing order):
 13, 15, 16, 16, 19, 20, 20, 21, 22, 22, 25, 25, 25, 25,30, 33, 33, 35,
, , , , , , , , , , , , , , , , , ,
35, 35, 35, 36, 40, 45, 46, 52, 70.
 Use binning (by bin means) to smooth the above data using a bin
data,
depth of 3.
 Illustrate your steps, and comment on the effect of this technique for
the given data
data.
Data Mining - R. Akerkar 15

16. Data Integration
g
 Data integration:
 combines data from multiple sources into a coherent store
 Schema integration
 Entity identification
E tit id tifi ti problem: identify real world entities f
bl id tif l ld titi from
multiple data sources, e.g., A.cust-id  B.cust-#
 integrate metadata from different sources
 Detecting and resolving data value conflicts
 for the same real world entity, attribute values from different
sources
so rces are different
 possible reasons: different representations, different scales,
e.g., metric vs. British units
Data Mining - R. Akerkar 16

17. Handling Redundancy in Data Integration
 Redundant data occur often when integration of multiple databases
 The same attribute may have different names in different
databases
 One attribute may be a “derived” attribute in another table e g
derived table, e.g.,
annual revenue
 Redundant data may be able to be detected by correlation analysis
 Careful integration of the data from multiple sources may help
reduce/avoid redundancies and inconsistencies and improve mining
speed and quality
Data Mining - R. Akerkar 17

18. Correlation Analysis
 Redundancies can be detected by this method.
 Given two attributes, such analysis can measure how strongly one
attribute implies the other, based on available data.
 The correlation between attributes A and B can be measured by
 Where n is number of tuples, and are respective mean values
of A and B, and and are the respective standard deviations
of A and B
Data Mining - R. Akerkar 18

19. Correlation Analysis
 If the resulting value of the equation is greater than 0, then A and B
are positively correlated.
 i.e. the l
i th values of A i
f increase as th values of B i
the l f increase.
 The higher the value, the more each attribute implies the other.
 Hence, high value may indicate that A (or B) may be removed as
redundancy.
redundancy
 If the resulting value is equal to zero, then A and B are independent
 There is no correlation between them.
 If the resulting value is less than zero, then A and B are negatively
correlated.
 i.e. the values of one attribute increase as the values of other attribute
decrease.
 Each attribute discourages the other.
Data Mining - R. Akerkar 19

20. Correlation Analysis
Above are three possible relationships between data. The graphs of high positive
and negative correlation are approaching a value of 1 and -1 respectively. The
graph showing no correlation has a value of 0.
Data Mining - R. Akerkar 20

21. Categorical Data
 To find the correlation between two categorical attributes we make
use of contingency tables.
g y
 Let us consider the following:
 Let there be 4 car manufacturers given by the set
{A,B,C,D} and let there be three segments of cars
manufactured by these companies given by the set
{S,M,L},
{S M L} where S stands for small cars M stands for
cars,
medium sized cars and L stands for Large cars.
 Observer collects data about the cars passing by,
manufactured by these companies and categorize them
according to their sizes.
Data Mining - R. Akerkar 21

22.  For finding the correlation between car manufacturers and the
size of cars that they manufacture we formulate a hypothesis,
that the size of car manufactured and the companies that
manufacture the cars are independent of each other
other.
 In other terms, we are saying that there is absolutely no
correlation between the car manufacturing company and the size
of the cars that they manufacture.
 Such a hypothesis in statistical terms is called the null
hypothesis and is denoted by Ho Ho.
 Null hypothesis: The car size and car manufacturers are
attributes independent of each other.
other
Data Mining - R. Akerkar 22

23. Data Transformation
 Smoothing: remove noise from data (binning and regression)
 Aggregation: summarization data cube construction
summarization,
 E.g. Daily sales data aggregated to compute monthly and annual total
amount.
 Generalization: concept hierarchy climbing
 Normalization is useful for classification algorithms involving neural nets,
clustering etc..
 Normalization: attribute data are scaled to fall within a small, specified range
such as – 1.0 to 1.0
 min-max normalization
 z-score normalization
 normalization by decimal scaling
 Attribute/feature construction
 New attributes constructed f
from the given ones
Data Mining - R. Akerkar 23

24. Data Transformation: Normalization
 min-max normalization (This type of normalization transforms the data into a
desired range, usually [0,1]. )
v  minA
v'  (new _ maxA  new _ minA)  new _ minA
maxA  minA
where, [minA, maxA] is the initial range and [new_minA, new_maxA] is the
,[ , ] g [ , ]
new range.
e.g.: If v = 73600 in [12000, 98000] Then v’ = 0.716 in the range [0, 1].
Here value for “income” is transformed to 0.716
It preserves the relationship among th original d t values.
th l ti hi the i i l data l
Data Mining - R. Akerkar 24

25. z-score normalization
By using this type of normalization, the mean of the transformed set
of data points is reduced to zero. For this, the mean and
standard deviation of the initial set of data values are required.
The t
Th transformation formula is
f ti f l i
v  mean A
v'
stand _ dev A
Where, meanA and std_devA are the mean and standard deviation
of the initial data values.
e.g.: If meanIncome = 54000, and std_devIncome = 16000, then v
= 76000 transformed to v’ =1.225.
This is useful when the actual min and max of attribute are
unknown.
Data Mining - R. Akerkar 25

26. Normalisation by Decimal Scaling
 This type of scaling transforms the data into a range between [-
1,1]. The transformation formula is
v
v' j
10
Where j is the smallest integer such that Max(| v' |)<1
 e.g.: Suppose recorded value of A is in initial range [-991, 99], k is
3, and v = -991 becomes v' = -0.991.
 The
Th mean absolute value of A is 991.
b l t l f i 991
 To normalise, we divide each value by 1000 (i.e. j = 3) so -991
normalises -0.991
Data Mining - R. Akerkar 26

27. Exercise 2
 Using the data for Age in previous Question, answer the following:
a) Use min-max normalization to transform the value 35 for age into the
range [0.0; 1.0].
b) Use z-score normalization to transform the value 35 for age, where
the standard deviation of age is 12.94.
c) Use normalization by decimal scaling to transform the value 35 for
age.
d) Comment on which method you would prefer to use for the given
data, giving reasons as to why.
Data Mining - R. Akerkar 27

28. What Is Prediction?
 Prediction is similar to classification
 First, construct a model
 Second, use model to predict unknown value
 Major method for prediction is regression
 Linear and multiple regression
 Non-linear regression
 Prediction is different from classification
P di ti i diff tf l ifi ti
 Classification refers to predict categorical class label
 Prediction models continuous-valued functions
 E.g. A model to predict the salary of university graduate with 15 years of
work experience.
Data Mining - R. Akerkar 28

29. Regression
 Regression shows a relationship between the average values of
two variables.
 Thus regression is very useful in estimating and predicting the
average value of one variable for a given value of other variable.
 The estimate or prediction may be made with the help of a
regression line.
 There are two types of variables in regression analysis-
independent variable and dependent variable.
 The variable whose value is to be predicted is called dependent
variable and th variable whose value i used f prediction i
i bl d the i bl h l is d for di ti is
called independent variable.
Data Mining - R. Akerkar 29

30.  Linear regression: If the regression curve is a straight
g g g
line, then there is a linear regression between two variables.
 Linear regression models a random variable, Y (called
variable
response variable) as a linear function of another random
variable, X ( called a predictor variable)
 Y=+X
 Two parameters ,  and  specify the line and are to
be estimated by using the data at hand. (regression
coefficients)
 The variance of Y is assumed to be constant.
 Th coefficients can be solved f
The ffi i t b l d for b th method of
by the th d f
least squares (minimizes the error between the actual
data and the estimate of the line. )
Data Mining - R. Akerkar 30

31. Linear Regression
 Given s samples or data points of the form (x1, y1), (x2, y2) …(xs, ys)
 The regression coefficients can be estimated as,
 Where is the average of x1, x2 … and is the average of y1,
y2,…
Data Mining - R. Akerkar 31

32. Multiple Regression
 Multiple regression: Y =  + 1 X1 + 2 X2.
p g
 Many nonlinear functions can be transformed into the
above.
 The regression analysis for studying more than
two variables at a time
time.
 It involves more than one predictor variable.
 Method of least square can be applied to solve for
, 1, and 2.
Data Mining - R. Akerkar 32

33. Non-Linear Regression
 If the curve of regression is not a straight line, i.e., a first degree
equation in the variables x and y, then it is called a non-linear
regression or curvilinear regression
 Consider a cubic polynomial relationship,
 Y =  +  1X +  2X2 +  3X3.
 To convert above equation in linear form, we define new variable:
 X1 = X, X2 = X2, X3 = X3
 Thus we get,
g
 Y =  +  1X1 +  2 X2+  3 X3.
 This is solvable by the method of least squares
squares.
Data Mining - R. Akerkar 33

34. Exercise 3
 Following table shows a set of X Y
paired data where X is the number Years Experience Salary (in $ 1000s)
of years of work experience of a 3 30
college graduates and Y is the 8 57
corresponding salary of the 9 64
graduate.
13 72
 Draw a graph of the data. Do X 3 36
and Y seem to have a linear
6 43
relationship?
11 59
 Also, predict the salary of a
21 90
college graduate with 10 years of
1 20
experience.
experience
16 83
Data Mining - R. Akerkar 34

35. Assignment
X Y
Midterm exam Final exam
 The following table shows the midterm and 72 84
final exam grades obtained for students in a 50 63
data mining course. 81 77
74 78
1. Plot the data. Do X and Y seem to have a 94 90
linear relationship? 86 75
2. Use the method of least squares to find an 59 49
equation for the prediction of a student’s
student s 83 79
final grade based on the student’s midterm 65 77
grade in the course. 33 52
3. Predict the final grade of a student who
g 88 74
received an 86 on the midterm exam. 81 90
Data Mining - R. Akerkar 35