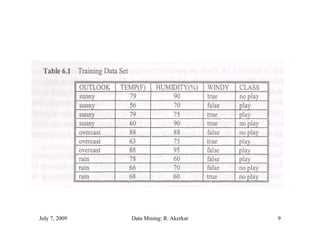
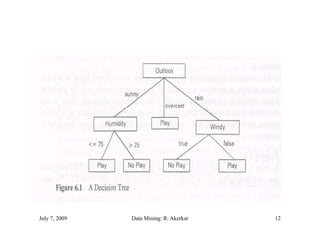
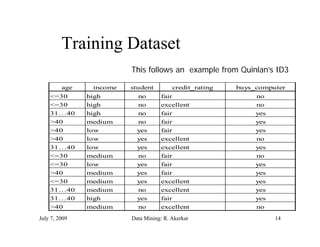
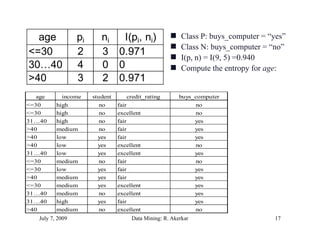
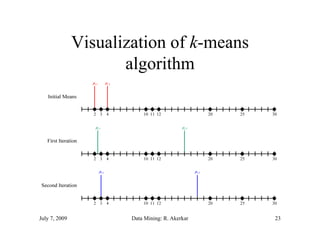
The document discusses data mining and classification techniques. It defines data mining as the extraction of interesting patterns from large amounts of data. Classification involves using attributes of records in a training dataset to predict the class of new, unseen records. Decision trees are a common classification technique that use attributes to recursively split data into subgroups until each subgroup belongs to a single class. The document also discusses clustering, which organizes unlabeled data into groups without predefined classes.

1. Data Mining
Rajendra Akerkar
July 7, 2009 Data Mining: R. Akerkar 1

2. What Is Data Mining?
• Data mining (knowledge discovery from data)
– Extraction of interesting (non-trivial, implicit,
previously unknown and potentially useful) patterns or
knowledge from huge amount of data
• Is everything “data mining”?
– (Deductive) query processing.
processing
– Expert systems or small ML/statistical programs
July 7, 2009 Data Mining: R. Akerkar 2

3. Definition
• Several Definitions
– Non-trivial extraction of implicit, previously
unknown and potentially useful information from data
– Exploration & analysis, by automatic or
semi automatic
semi-automatic means, of
large quantities of data
in order to discover
meaningful patterns
July 7, 2009 Data Mining: R. Akerkar 3

4. From [Fayyad, et.al.] Advances in Knowledge Discovery and Data Mining, 1996
[ yy , ] g y g,
July 7, 2009 Data Mining: R. Akerkar 4

5. Classification
July 7, 2009 Data Mining: R. Akerkar 5

6. Classification: D fi iti
Definition
• Given a collection of records (training set )
– Each record contains a set of attributes, one of the
attributes is the class.
• Find a model for class attribute as a function of the
values of other attributes.
• Goal: pre io sl unseen records should be assigned
previously nseen sho ld
a class as accurately as possible.
– A test set is used to determine the accuracy of the model.
y
Usually, the given data set is divided into training and
test sets, with training set used to build the model and
test set used to validate it.
July 7, 2009 Data Mining: R. Akerkar 6

7. Classification: Introduction
• A classification scheme which generates a tree
and a set of rules from given data set.
• The attributes of the records are categorise into
two types:
– Attributes whose domain is numerical are called
numerical attributes.
– A ib
Attributes whose domain is not numerical are
h d i i i l
called the categorical attributes.
July 7, 2009 Data Mining: R. Akerkar 7

8. Decision Tree
• A decision tree is a tree with the following properties:
– An inner node represents an attribute.
– A edge represents a t t on the attribute of the father
An d t test th tt ib t f th f th
node.
– A leaf represents one of the classes.
• Construction of a decision tree
– Based on the training data
– Top-Down strategy
July 7, 2009 Data Mining: R. Akerkar 8

9. July 7, 2009 Data Mining: R. Akerkar 9

10. Decision Tree
Example
• The data set has five attributes.
• There is a special attribute: the attribute class is the class
label.
label
• The attributes, temp (temperature) and humidity are
numerical attributes
• Other attributes are categorical, that is, they cannot be
categorical is
ordered.
• Based on the training data set, we want to find a set of
set
rules to know what values of outlook, temperature,
humidity and wind, determine whether or not to play golf.
July 7, 2009 Data Mining: R. Akerkar 10

11. Decision Tree
Example
• We have five leaf nodes.
• In a decision tree, each leaf node represents a rule.
, p
• We have the following rules corresponding to the tree
given in Figure.
• RULE 1 If it is sunny and the humidity is not above 75%, then play.
• RULE 2 If it is sunny and the humidity is above 75%, then do not play.
f y y , p y
• RULE 3 If it is overcast, then play.
• RULE 4 If it is rainy and not windy, then play.
• RULE 5 If it is rainy and windy, then don't play.
July 7, 2009 Data Mining: R. Akerkar 11

12. July 7, 2009 Data Mining: R. Akerkar 12

13. Iterative Dichotomizer (ID3)
• Quinlan (1986)
• Each d
E h node corresponds to a splitting attribute
d t litti tt ib t
• Each arc is a possible value of that attribute.
• At each node the splitting attribute is selected to be the most
informative among the attributes not yet considered in the path from
the root.
• Entropy is used to measure how informative is a node.
• The algorithm uses the criterion of information gain to determine
the goodness of a split.
– The attribute with the greatest information gain is taken as
g g
the splitting attribute, and the data set is split for all distinct
values of the attribute.
July 7, 2009 Data Mining: R. Akerkar 13

14. Training Dataset
This follows an example from Quinlan’s ID3
age income student credit_rating buys_computer
<=30 high no fair no
<=30 g
high no excellent no
31…40 high no fair yes
>40 medium no fair yes
>40 low yes fair yes
>40 low yes excellent no
31…40 low yes excellent yes
<=30 medium no fair no
<=30 low yes fair yes
>40 medium yes fair yes
<=30 medium yes excellent yes
31…40 medium no excellent yes
31…40 g
high y
yes fair y
yes
>40 medium no excellent no
July 7, 2009 Data Mining: R. Akerkar 14

15. Extracting Classification Rules from
Trees
• Represent the k
R h knowledge in the
l d i h
form of IF-THEN rules
• One rule is created for each path
from the root to a leaf
• Each attribute-value pair along a
path forms a conjunction
• The leaf node holds the class
prediction
• Rules
R l are easier for humans to
i f h
understand What are the rules?
July 7, 2009 Data Mining: R. Akerkar 15

16. Attribute Selection Measure: Information
Gain (ID3/C4.5)
(ID3/C4 5)
 Select the attribute with the highest information gain
 S contains si tuples of class Ci for i = {1, …, m}
 information measures info required to classify any
q y y
arbitrary tuple m
si si
I( s1,s 2,...,s m )    log 2

i 1 s s ….information is encoded in bits.
 entropy of attribute A with values {a1,a2,…,av}
f b h l {
v
s1 j  ... smj
E(A)  I( s1 j ,...,smj )
j 1 s
 information gained by branching on attribute A
Gain(A)  I(s 1, s 2 ,..., sm)  E(A)
July 7, 2009 Data Mining: R. Akerkar 16

17. age pi ni I(pi, ni)  Class P: buys_computer = “yes”
 Cl
Class N: buys_computer = “no”
N b t “ ”
<=30 2 3 0.971  I(p, n) = I(9, 5) =0.940
30…40 4 0 0  Compute the entropy for age:
>40 3 2 0 971
0.971
age income student credit_rating buys_computer
<=30 high
g no fair no
<=30 high no excellent no
31…40 high no fair yes
>40 medium no fair yes
>40 low
ow yes fair yes
>40 low yes excellent no
31…40 low yes excellent yes
<=30 medium no fair no
< 30
<=30 low yes fair yes
>40 medium yes fair yes
<=30 medium yes excellent yes
31…40 medium no excellent yes
31…40
31 40 high yes fair yes
>40 medium no excellent no
July 7, 2009 Data Mining: R. Akerkar 17

18. Attribute Selection by Information Gain
Computation
5 4
E ( age ) 
g I ( 2 ,3)  I ( 4,0 )
14 14
5
 I (3, 2 )  0 .694
14
5
I ( 2 ,3 ) means “age <=30” has 5 out of 14 samples, with 2 yes's
14
and 3 no’s. Hence
Gain ( age )  I ( p , n )  E ( age )  0.246
Similarly, Gain(income)  0.029
Gain( student )  0.151
Gain(credit _ rating )  0.048
July 7, 2009 Data Mining: R. Akerkar 18

19. Exercise 1
• The following table consists of training data from an employee
database.
database
• Let status be the class attribute. Use the ID3 algorithm to construct
a decision tree from the given data.
July 7, 2009 Data Mining: R. Akerkar 19

20. Clustering
July 7, 2009 Data Mining: R. Akerkar 20

21. Clustering: Definition
• Given a set of data points, each having a set of
attributes, and a similarity measure among them, find
clusters such that
– Data points in one cluster are more similar to one another.
– Data points in separate clusters are less similar to one
another.
h
• Similarity Measures:
– E lid
Euclidean Distance if attributes are continuous.
Di t tt ib t ti
– Other Problem-specific Measures.
July 7, 2009 Data Mining: R. Akerkar 21

22. The K-Means Clustering Method
K Means
• Given k, the k-means algorithm is implemented in
k means
four steps:
– Partition objects into k nonempty subsets
– Compute seed points as the centroids of the clusters of
the current partition (the centroid is the center, i.e., mean
center i e
point, of the cluster)
– Assign each object to the cluster with the nearest seed
point
– Go back to Step 2, stop when no more new assignment
July 7, 2009 Data Mining: R. Akerkar 22

23. Visualization of k-means
k means
algorithm
July 7, 2009 Data Mining: R. Akerkar 23

24. Exercise 2
• Apply the K-means algorithm for the
following 1-dimensional points (for k=2): 1;
g p ( ) ;
2; 3; 4; 6; 7; 8; 9.
• Use 1 and 2 as the starting centroids.
centroids
July 7, 2009 Data Mining: R. Akerkar 24

25. K – Mean for 2-dimensional
2 dimensional
database
• Let us consider {x1, x2, x3, x4, x5} with following coordinates as
two-dimensional sample for clustering:
• x1 = (0, 2), x2 = (0, 0), x3 = (1.5,0), x4 = (5,0), x5 = (5, 2)
• Suppose that required number of clusters is 2.
• Initially, clusters are formed from random distribution of
samples:
• C1 = {x1, x2, x4} and C2 = {x3, x5}.
July 7, 2009 Data Mining: R. Akerkar 25

26. Centroid Calculation
• Suppose that the given set of N samples in an n-dimensional space
has somehow be partitioned into K clusters {C1, C2, …, Ck}
• Each Ck has nk samples and each sample is exactly in one cluster.
• Therefore,  nk = N, where k = 1, …, K.
• The mean vector Mk of cluster Ck is defined as centroid of the
cluster, nk
Mk = (1/ nk)  i = 1 xik
Where xik is the ith sample belonging
to cluster Ck.
• In our example The centroids for these two clusters are
example,
• M1 = {(0 + 0 + 5)/3, (2 + 0 + 0)/3} = {1.66, 0.66}
• M2 = {( 1.5 + 5)/2, (0 +2)/2} = {3.25, 1.00}
) ( ) } { }
July 7, 2009 Data Mining: R. Akerkar 26

27. The S
Th Square-error of th cluster
f the l t
• The square-error for cluster Ck is the sum of squared Euclidean
distances between each sample in Ck and its centroid.
• Thi error is called the within-cluster variation.
This i ll d th ithi l t i ti
ek2 = n k
i=1 (xik – Mk)2
• Within cluster variations, after initial random distribution of
samples, are
• e12 = [(0 – 1.66)2 + (2 – 0.66)2] + [(0 – 1.66)2 + (0 – 0.66)2]
+ [(5 – 1.66)2 + (0 – 0.66)2] = 19.36
• e22 = [(1.5 – 3.25)2 + (0 – 1)2] + [( – 3.25)2 + (2 – 1)2] = 8.12
[( ) ( ) [(5 ) ( )
July 7, 2009 Data Mining: R. Akerkar 27

28. Total Square-error
• The square error for the entire clustering space
containing K clusters is the sum of the within-cluster
variations. K
i i
Ek2 = 
k = 1 ek
2
• The total square error is
E2 = e12 + e22 = 19.36 + 8.12 = 27.48
July 7, 2009 Data Mining: R. Akerkar 28

29. • When we reassign all samples, depending on a minimum distance
from centroids M1 and M2, the new redistribution of samples inside
clusters will be,
be
• d(M1, x1) = (1.662 + 1.342)1/2 = 2.14 and d(M2, x1) = 3.40  x1  C1
• d(M1, x2) = 1.79 and d(M2, x2) = 3.40  x2  C1
d(M1, x3) = 0.83 and d(M2, x3) = 2.01  x3  C1
d(M1, x4) = 3.41 and d(M2, x4) = 2.01  x4  C2
d(M1, x5) = 3.60 and d(M2, x5) = 2.01  x5  C2
Above calculation is based on Euclidean distance formula,
d(xi, xj) = k = 1 (xik – xjk)1/2
m
July 7, 2009 Data Mining: R. Akerkar 29

30. • New Clusters C1 = {x1, x2, x3} and C2 = {x4, x5} have new
centroids
• M1 = {0.5, 0.67}
• M2 = {5.0, 1.0}
• The corresponding within-cluster variations and the total square
error are,
• e12 = 4.17
• e22 = 2.00
• E2 = 6.17
July 7, 2009 Data Mining: R. Akerkar 30

31. Exercise 3
Let the set X consist of the following sample points in 2
dimensional space:
X = {(1, 2), (1.5, 2.2), (3, 2.3), (2.5,-1), (0, 1.6), (-1,1.5)}
Let c1 = (1.5, 2.5) and c2 = (3, 1) be initial estimates of
centroids for X.
What are the revised values of c1 and c2 after 1 iteration of k-
means clustering (k = 2)?
July 7, 2009 Data Mining: R. Akerkar 31

32. Association Rule Discovery
July 7, 2009 Data Mining: R. Akerkar 32

33. Associations discovery
• Associations discovery uncovers affinities
amongst collection of items
• Affinities are represented by association rules
• Associations discovery is an unsupervised
approach to data mining.
July 7, 2009 Data Mining: R. Akerkar 33

34. Association discovery is one of the most common
forms of data mining that people closely
associate with data mining, namely mining for
gold through a vast database. The gold in this
ld th h td t b Th ld i thi
case is a rule that tells you something about your
database that you did not already know, and
know
were probably unable to explicitly articulate
July 7, 2009 Data Mining: R. Akerkar 34

35. Association discovery is done using rule induction which
y g
basically tells a user how strong a pattern is and how
likely it is to happen again. For instance a database of
items scanned in a consumer market basket helps finding
interesting patterns such as: If bagels are purchased then
cream cheese is purchased 90% of the time and this
pattern occurs i 3% of all shopping baskets
in f ll h i b k
You go tell the data base to go find the rules, the rules that are
rules
pulled from the database are extracted and ordered to be
presented to the user to according to the percentage of
times they are correct and how often they apply. Often
gets lot of rules and the user almost needs a second pass
to find his/her gold nugget.
g gg
July 7, 2009 Data Mining: R. Akerkar 35

36. Associations
• The problem of deriving associations from
data
– market-basket analysis
– The popular algorithms are thus concerned with
determining the set of frequent itemsets in a
given set of operation databases.
– The problem is to compute the frequency of
occurrences of each itemset in the database.
July 7, 2009 Data Mining: R. Akerkar 36

37. Definition
July 7, 2009 Data Mining: R. Akerkar 37

38. Association Rules
• Algorithms that obtain association rules
from data usually divide the task into two
y
parts:
– find the frequent itemsets and
– form the rules from them.
July 7, 2009 Data Mining: R. Akerkar 38

39. Association Rules
• The problem of mining association rules can be
divided into two sub-problems:
July 7, 2009 Data Mining: R. Akerkar 39

40. a priori Algorithm
July 7, 2009 Data Mining: R. Akerkar 40

41. Exercise 3
Suppose that L3 is the list
{{a,b,c}, {a,b,d}. {a,c,d}, {b,c,d}. {b,c,w},
{b,c,x}, {p,q,r}, {p,q,s}, {p,q,t}, {p,r,s},
{q,r,s}}
Which itemsets are placed in C4 by the join
step of the Apriori algorithm? Which are
p p g
then removed by the prune step?
July 7, 2009 Data Mining: R. Akerkar 41

42. Exercise 4
• Given a dataset with four attributes w, x, y
and z, each with three values, how many
, , y
rules can be generated with one term on the
right-hand side?
g
July 7, 2009 Data Mining: R. Akerkar 42

43. References
• R. Akerkar and P. Lingras. Building an Intelligent Web: Theory &
Practice, Jones & Bartlett, 2008 (In India: Narosa Publishing House,
2009)
• U. M. Fayyad, G. Piatetsky-Shapiro, P. Smyth, and R. Uthurusamy.
Advances in Knowledge Discovery and Data Mining. AAAI/MIT Press,
Mining Press
1996
• U. Fayyad, G. Grinstein, and A. Wierse, Information Visualization in
Data Mining and Knowledge Discovery, Morgan Kaufmann, 2001
• J. Han and M. Kamber. Data Mining: Concepts and Techniques. Morgan
Kaufmann, 2001
K f
• D. J. Hand, H. Mannila, and P. Smyth, Principles of Data Mining, MIT
Press, 2001
,
July 7, 2009 Data Mining: R. Akerkar 43