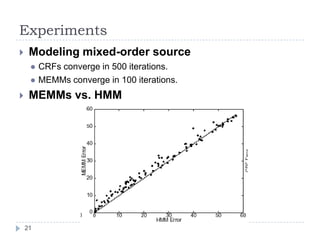
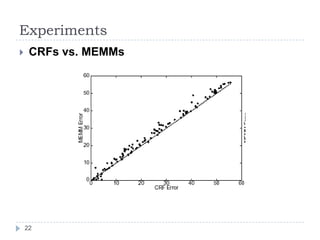
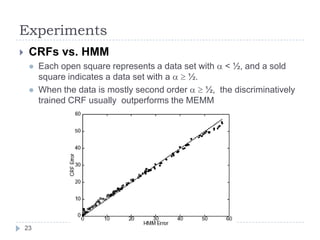
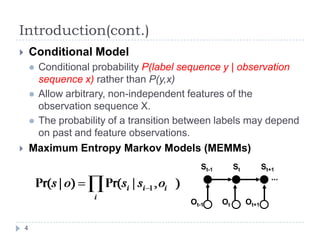
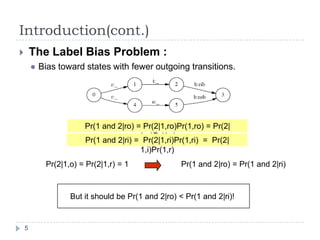
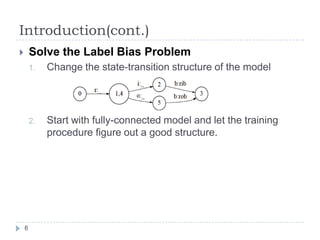
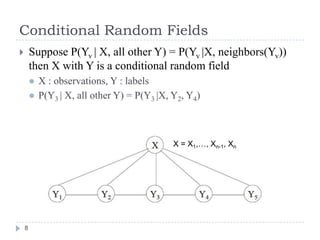
Conditional random fields (CRFs) are probabilistic models for segmenting and labeling sequence data. CRFs address limitations of previous models like hidden Markov models (HMMs) and maximum entropy Markov models (MEMMs). CRFs allow incorporation of arbitrary, overlapping features of the observation sequence and label dependencies. Parameters are estimated to maximize the conditional log-likelihood using iterative scaling or tracking partial feature expectations. Experiments show CRFs outperform HMMs and MEMMs on synthetic and real-world tasks by addressing label bias problems and modeling dependencies beyond the previous label.

1. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence DataJohn Lafferty, Andrew McCallum, Fernando PereiraSpeaker : Shu-Ying Li1

2. OutlineIntroductionConditional Random FieldsParameter Estimated for CRFsExperimentsConclusions2

3. IntroductionSequence Segmenting and LabelingGoal : mark up sequences with content tags.Generative ModelsHidden Markov Model (HMM) and stochastic grammars

4. Assign a joint probability to paired observation and label sequences

5. The parameters typically trained to maximize the joint likelihood of train examplesSt-1StSt+1OtOt+13

6. Introduction(cont.)Conditional ModelConditional probability P(label sequence y | observation sequence x)rather than P(y,x)

7. Allow arbitrary, non-independent features of the observation sequence X.

8. The probability of a transition between labels may depend on past and feature observations.Maximum Entropy Markov Models (MEMMs)St-1StSt+1...OtOt+1Ot-14

9. Introduction(cont.)The Label Bias Problem:Bias toward states with fewer outgoing transitions.Pr(1 and 2|ro) = Pr(2|1,ro)Pr(1,ro) = Pr(2| 1,o)Pr(1,r)Pr(1 and 2|ri) = Pr(2|1,ri)Pr(1,ri) = Pr(2| 1,i)Pr(1,r)Pr(2|1,o) = Pr(2|1,r) = 1Pr(1 and 2|ro) = Pr(1 and 2|ri) But it should be Pr(1 and 2|ro) < Pr(1 and 2|ri)! 5

10. Introduction(cont.)Solve the Label Bias ProblemChange the state-transition structure of the modelStart with fully-connected model and let the training procedure figure out a good structure.6

11. Conditional Random FieldsRandom FieldLet G = (Y, E) be a graph where each vertex Yv is a random variable. Suppose P(Yv| all other Y) = P(Yv| neighbors(Yv)) then Y is a random field.Example :P(Y5 | all other Y) = P(Y5 | Y4, Y6)7

12. Conditional Random FieldsSuppose P(Yv| X, all other Y) = P(Yv|X, neighbors(Yv)) then X with Y is a conditional random fieldX : observations, Y : labels

13. P(Y3 | X, all other Y) = P(Y3 |X, Y2, Y4)X = X1,…, Xn-1, Xn8

14. Conditional Random Fields9Conditional Distribution[2]tj(yi−1, yi, x, i) is a transition feature function of the entire observation sequence and the labels at positions i and i−1 in the label sequence

15. sk(yi, x, i) is a state feature function of the label at position i and the observation sequence

16. λkand μkare parameters to be estimated from training data.Conditional Distribution[1]x : data sequence

17. y : label sequence

18. v : vertex from vertex set V

19. e : edge from edge set E over V

20. fk: Boolean vertex feature; gk : Boolean edge feature

21. k : the number of features

22. λk and μk are parameters to be estimated

23. y|e is the set of components of y defined by edge e

24. y|v is the set of components of y defined by vertex vYt-1YtYt+1...XtXt+1Xt-1

25. Conditional Random FieldsConditional DistributionCRFs use Z(x) for the conditional distributions

26. Z(x) is a normalization over the data sequence x