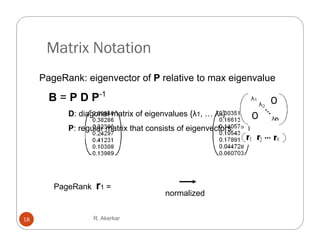
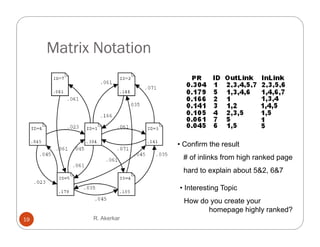
This document provides an overview of link analysis and summarizes several common approaches: 1. Early approaches calculated site popularity based on incoming and outgoing links, but had limitations in accounting for link importance. HITS introduced the concepts of hubs and authorities, where authoritative sites receive links from important hubs. 2. PageRank assigns weight based on the rank of parent sites, inversely proportional to their outdegree. It models the probability of a random web surfer being on a page. 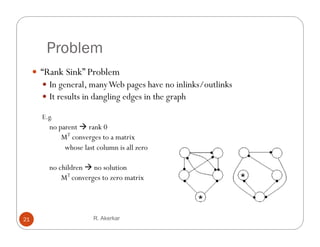3. Link analysis approaches like HITS and PageRank have limitations, such as failing to account for dangling nodes with no links. Modifications include adding a small probability of randomly restarting from any page.

1. Link Analysis
Rajendra Akerkar
Vestlandsforsking, Norway

2. Objectives
 To review common approaches to l k analysis
h link l
 To calculate the popularity of a site based on link
analysis
 To model human judgments indirectly
2 R. Akerkar

3. Outline
1.
1 Early Approaches to Link Analysis
2. Hubs and Authorities: HITS
3. Page Rank
4. Stability
5. Probabilistic Link Analysis
6. Limitation of Link Analysis
3 R. Akerkar

4. Early Approaches
Basic Assumptions
• Hyperlinks contain information about the human
judgment of a site
• The more incoming links to a site the more it is
site,
judged important
Bray 1996
y
• The visibility of a site is measured by the number
of other sites pointing to it
• The luminosity of a site is measured by the number
of other sites to which it points
 Limitation: failure to capture the relative
importance of different parents (children) sites
4 R. Akerkar

5. Early Approaches
Mark 1988
• To calculate the score S of a document at vertex v
1
S(v) = s(v) + Σ S(w)
| ch[v] | w Є |ch(v)|
v: a vertex i the h
in h hypertext graph G = (V E)
h (V,
S(v): the global score
s(v): the score if the document is isolated
ch(v): children of the document at vertex v
• Limitation:
- Require G to be a directed acyclic g p (
q y graph (DAG)
)
- If v has a single link to w, S(v) > S(w)
- If v has a long path to w and s(v) < s(w),
then S(v) > S (w)
 unreasonable
5 R. Akerkar

6. Early Approaches
Marchiori (1997)
• Hyper information should complement textual
information to obtain the overall information
S(v) = s(v) + h(v)
( ) ( ) ( )
- S(v): overall information
- s(v): textual information
- h(v): hyper information
r(v, w)
• h(v) = Σ F S(w)
w Є |ch[v]|
- F a fading constant F Є (0 1)
F: constant, (0,
- r(v, w): the rank of w after sorting the children
of v by S(w)
 a remedy of the previous approach (Mark 1988)
6 R. Akerkar

7. HITS - Kleinberg’s Algorithm
• HITS – Hypertext Induced Topic Selection
yp p
• For each vertex v Є V in a subgraph of interest:
a(v) - the authority of v
h(v) - the hubness of v
• A site is very a thoritati e if it recei es man
er authoritative receives many
citations. Citation from important sites weight
more than citations from less-important sites
• Hubness shows the importance of a site. A good
hub is a site that links to many authoritative sites
y
7 R. Akerkar

8. Authority and Hubness
2 5
3 1 1 6
4
7
a(1) = h(2) + h(3) + h(4) h(1) = a(5) + a(6) + a(7)
8 R. Akerkar

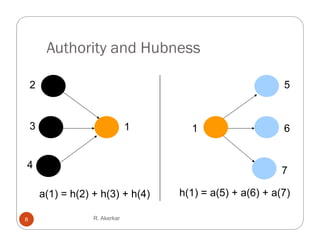
9. Authority d H b
A th it and Hubness Convergence
C g
• R
Recursive d
i dependency:
d
a(v)  Σ h(w)
w Є pa[v]
h(v)  Σ w Є ch[v] a(w)
• Using Linear Algebra, we can prove:
a(v) and h(v) converge
9 R. Akerkar

10. HITS Example
Find a base subgraph:
• Start with a root set R {1, 2, 3, 4}
• {1, 2, 3, 4} - nodes relevant to
the topic
• Expand the root set R to include
all the children and a fixed
number of parents of nodes in R
 A new set S (base subgraph) 
10 R. Akerkar

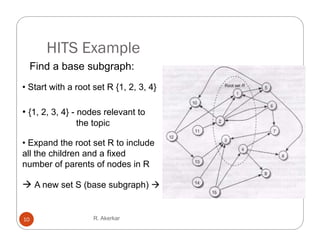
11. HITS Example
BaseSubgraph( R d)
R,
1. S  r
2. for each v in R
3. do S  S U ch[v]
4. P  pa[v]
5. if |P| > d
f
6. then P  arbitrary subset of P having size d
7. SSUP
8.
8 return S
11 R. Akerkar

12. HITS Example
Hubs and authorities: two n-dimensional a and h
HubsAuthorities(G)
|V|
1 1  [1,…,1] Є R
2 a0  h 0  1
3 t 1
4 repeat
5 for each v in V
6 do at (v)  Σ h (w)
w Є pa[v] t -1
7 ht (v)  Σ w Є pa[v] a (w)
8 a t  at / || at || t -1
9 h t  ht / || ht ||
10 t  t+1
11 until || a t – at -1 || + || h t – ht -1 || < ε
1 1
12 return (a t , h t )
12 R. Akerkar

13. HITS Example Results
y
Authority
Hubness
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Authority and hubness weights
13 R. Akerkar

14. HITS Improvements
Brarat and Henzinger (1998)
• HITS problems
1) The document can contain many identical links to
the same document in another host
2) Links are generated automatically (e.g. messages
posted on newsgroups)
• Solutions
1) Assign weight to identical multiple edges, which
are inversely proportional to their multiplicity
2) Prune irrelevant nodes or regulating the influence
of a node with a relevance weight
14 R. Akerkar

15. PageRank
 Introduced by Page et al (
y g (1998))
 The weight is assigned by the rank of parents
 Difference with HITS
 HITS takes Hubness & Authority weights
 The page rank is proportional to its parents’ rank, but inversely
proportional to its parents’ outdegree
15

16. Matrix Notation
Adjacent M i
Adj Matrix
A=
* http://www.kusatro.kyoto-u.com
16

17. Matrix Notation
 Matrix Notation
r=αBr=Mr
α : eigenvalue
r : eigenvector of B
Ax=λx
B=
| A - λI | x = 0
Finding Pagerank
 to find eigenvector of B with an associated eigenvalue α
17

18. Matrix Notation
PageRank: eigenvector of P relative to max eigenvalue
B = P D P-1
D: diagonal matrix of eigenvalues {λ1, … λn}
P: regular matrix that consists of eigenvectors
PageRank r1 =
normalized
18 R. Akerkar

19. Matrix Notation
• Confirm the result
# of inlinks from high ranked page
hard to explain about 5&2 6&7
5&2,
• Interesting Topic
How do you create your
homepage highly ranked?
19 R. Akerkar

20. Markov Chain Notation
 Random surfer model
 Description of a random walk through the Web graph
 Interpreted as a transition matrix with asymptotic probability that a
surfer is currently browsing that page
rt = M rtt-1
1
M: transition matrix for a first-order Markov chain (stochastic)
Does it converge to some sensible solution ( too)
g (as )
regardless of the initial ranks ?
20 R. Akerkar

21. Problem
 “Rank Sink” Problem
 In general, many Web pages have no inlinks/outlinks
 It results in dangling edges in the graph
E.g.
no parent  rank 0
MT converges to a matrix
whose last column is all zero
no children  no solution
MT converges to zero matrix
21 R. Akerkar

22. Modification
 Surfer will restart browsing by p
g y picking a new Web p g at
g page
random
M=(B+E)
E : escape matrix
M : stochastic matrix
 S ll problem?
Still bl
 It is not guaranteed that M is primitive
 If M is stochastic and primitive, PageRank converges to
corresponding stationary distribution of M
22 R. Akerkar

23. PageRank Algorithm
* Page et al 1998
al,
23 R. Akerkar

24. Distribution of the Mixture Model
 The probability distribution that results from combining the
p y g
Markovian random walk distribution & the static rank source
distribution
r = εe + (1- ε)x
1
ε: probability of selecting non-linked page
PageRank
Now, transition matrix [εH + (1- ε)M] is primitive and stochastic
rt converges to the dominant eigenvector
24 R. Akerkar

25. Stability
 Whether the link analysis algorithms based on eigenvectors
are stable in the sense that results don’t change significantly?
 Th connectivity of a portion of the graph is changed
The f f h h h d
arbitrary
 How will it affect the results of algorithms?
25 R. Akerkar

26. Stability of HITS
Ng et al (2001)
• A bound on the number of hyperlinks k that can added or deleted
from one page without affecting the authority or hubness weights
• It is possible to perturb a symmetric matrix by a quantity that grows
as δ that produces a constant perturbation of the dominant
eigenvector
δ: eigengap λ1 – λ2
g g p
d: maximum outdegree of G
26 R. Akerkar

27. Stability of PageRank
Ng et al (2001)
V: the set of vertices touched by the perturbation
 The parameter ε of the mixture model has a stabilization role
 If the set of pages affected by the p
pg y perturbation have a small rank, the overall
,
change will also be small
tighter bound by
Bianchini et al (2001)
δ(j) >= 2 depends on the edges incident on j
27 R. Akerkar

28. SALSA
 SALSA (Lempel, Moran 2001)
 Probabilistic extension of the HITS algorithm
 Random walk is carried out by following hyperlinks both in the
forward and in the backward direction
 Two separate random walks
 Hub walk
 Authority walk
28 R. Akerkar

29. Forming a Bipartite Graph in SALSA
29 R. Akerkar

30. Random Walks
 Hub walk
 Follow a Web link from a page uh to a page wa (a forward link)
and then
 Immediately traverse a backlink going from wa to vh, where (u w)
(u,w)
Є E and (v,w) Є E
 Authority Walk
y
 Follow a Web link from a page w(a) to a page u(h) (a backward
link) and then
 Immediately traverse a f
d l forward link going b k f
dl k back from vh to wa
where (u,w) Є E and (v,w) Є E
30 R. Akerkar

31. Computing Weights
 Hub weight computed from the sum of the product of the
inverse degree of the in-links and the out-links
31 R. Akerkar

32. Why We Care
 Lempel and Moran (2001) showed theoretically that SALSA
weights are more robust that HITS weights in the presence of the
Tightly Knit Community (TKC) Effect.
 This effect occurs when a small collection of pages (related to a given topic)
is connected so that every hub links to every authority and includes as a special
case the mutual reinforcement effect
 The pages in a community connected in this way can be ranked
highly by HITS, higher than pages in a much larger collection
HITS
where only some hubs link to some authorities
 TKC could be exploited by spammers hoping to increase their
page weight ( li k f
i h (e.g. link farms)
)
32 R. Akerkar

33. A Similar Approach
 Rafiei and Mendelzon (2000) and Ng et al. (2001)
propose similar approaches using reset as in
PageRank
 Unlike PageRank, in this model the surfer will
follow a forward link on odd steps but a
backward li k
b k d link on even steps t
 The stability properties of these ranking
distributions are similar to those of PageRank (Ng
et al. 2001)
33 R. Akerkar

34. Overcoming TKC
 Similarity downweight sequencing and sequential
y g g
clustering (Roberts and Rosenthal 2003)
 Consider the underlying structure of clusters
y g
 Suggest downweight sequencing to avoid the
Tight Knit Community problem
g yp
 Results indicate approach is effective for few
tested queries, but still untested on a large scale
34 R. Akerkar

35. PHITS and More
 PHITS: Cohn and Chang (2000)
 Only the principal eigenvector is extracted using SALSA, so the
authority along the remaining eigenvectors is completely
neglected
 Account for more eigenvectors of the co-citation matrix
 See also Lempel, Moran (2003)
35 R. Akerkar

36. Limits of Link Analysis
 META tags/ invisible text
 Search engines relying on meta tags in documents are often
misled (intentionally) by web developers
P f
Pay-for-place
l
 Search engine bias : organizations pay search engines and page
rank
 Advertisements: organizations pay high ranking pages for
advertising space
 W h a primary effect of increased visibility to end users and a secondary
With ff f d bl d d d
effect of increased respectability due to relevance to high ranking page
36 R. Akerkar

37. Limits of Link Analysis
 Stability
 Adding even a small number of nodes/edges to the graph has a
significant impact
 T i drift – similar t TKC
Topic d ift i il to
 A top authority may be a hub of pages on a different topic
resulting in increased rank of the authority p g
g y page
 Content evolution
 Adding/removing links/content can affect the intuitive
authority rank of a page requiring recalculation of page ranks
37 R. Akerkar

38. Further Reading
 R. Akerkar d P. Lingras, Building an I ll
R Ak k and P L B ld Intelligent W b Th
Web: Theory
and Practice, Jones & Bartlett, 2008
 http://www.jbpub.com/catalog/9780763741372/
p j p g
38 R. Akerkar