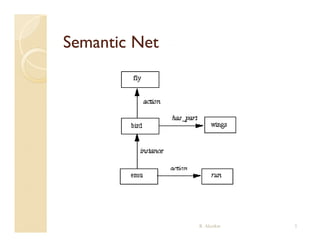
This document discusses description logics, which are knowledge representation languages that can represent domain knowledge in a structured, logical way. Description logics were designed as an extension of frames and semantic networks to add formal logic-based semantics. Description logics use individuals, concepts, and roles to represent knowledge. Concepts can be combined using constructors like conjunction and existential restrictions. Description logics allow logical inference through concept subsumption, where more specific concepts are subsumed by more general ones.

1. Description Logic
Rajendra Akerkar
j
Western Norway Research Institute, Norway

2. Knowledge Representation
 f
facilitate inferencing
f g
 Inferencing often involves making classes
o
of objects, defining a hierarchy, giving
e g e a c y, g v g
attributes to objects and specifying
constraints.
R. Akerkar 2

3. Predicate Calculus
 Uses (i) Predicates for describing relationships
and (ii) Rules for inferencing
 A special kind of inferencing is Inheritance
where all properties of a super class are passed
onto its subclasses
 For
F example, it can b inferred that men- b i
l i be i f d h being
human have 2 legs by virtue of their inheriting
human-properties.
human-properties
R. Akerkar 3

4. Structured Knowledge
Representation
 Components and their interrelationships have to
be expressed
 Semantic Nets and Frames prove more
effective than predicate calculus
 Reminiscent of calculus where using
differentiation to find the rate of change of one
q y p
quantity with respect to another is more
convenient than using the more foundational
y
Lt
L
x 0 x R. Akerkar 4

5. Semantic Net
R. Akerkar 5

6. Frames
(example f
l from medical entities dictionary, Columbia
di l i i di i C l bi
University)
Have slots and fillers
R. Akerkar 6

7. Motivation to study
 Structure of the knowledge may not be
visible, and obvious inferences may be difficult
to draw
 Expressive power is too high for obtaining
decidable and efficient inference
 Inference power may be too low f
I f b l for
expressing interesting, but still decidable
theories
R. Akerkar 7

8. Wikipedia Definition
 “Description logics (DL) are a family of knowledge
representation languages which can be used to
represent the terminological knowledge of an
application domain in a structured and formally well-
understood way. The name description logic refers on the
way refers,
one hand, to concept descriptions used to describe a
domain and, on the other hand, to the logic-based
semantics which can be given by a translati n int first
hich i en b translation into first-
order predicate logic. Description logic was designed as
an extension to frames and semantic networks, which
were not equipped with formal logic-based semantics.”
t i d ith f ll i b d ti ”
R. Akerkar 8

9. Constituents of DL
 Individuals (such as Ralf and John)
( f J )
 Concepts (such as Man and Woman)
 Roles (such as isStudent)
Individuals are like constants in predicate calculus,
while Concepts are like Unary predicates
and Roles are like Binary Predicates.
R. Akerkar 9

10. Constructors of DL and their
meaning
Constructor Syntax Example Semantics using PC
Atomic Concept A Human {x | human(x)}
Atomic Role R Has-child { y
{<x,y> | has-child(x,y)}
( y)}
Conjunction C∩D Human ∩ Male {x | human(x)  male(x)}
Disjunction CD Doctor  Lawyer {x | doctor(x)  lawyer(x)}
Negation C Male {x | male(x)}
Exists Restriction  R.C  Has-child.Male {x |  y has-child(x,y) 
male(y)}
Value Restriction  R.C Has-child.Doctor {x | y has-child(x,y)
doctor(y)}
R. Akerkar 10

11. Examples
 For example the set of all those p
p parents
having a male child who is a doctor or a
lawyer is expressed as
y p
 Has-child.Male ∩( Doctor U Lawyer)
R. Akerkar 11

12. Quantifiers and ‘Dots’
Dots
 HasChild.Girl is interpreted as the set
◦ {x | (y)( HasChild(x,y)Girl(y))} and
 isEmployedBy.Farmer is interpreted as
p y y p
◦ {x | (y)( isEmployedBy(x,y) Farmer(y))}
R. Akerkar 12

13. Inference in DL
 Main mechanism: Inheritance via subsumption
 DL suitable for ontology engineering
 A concept C subsumes a concept D iff
I(D)  I(C) on every interpretation I
 For example: Person subsumes Male, Parent
subsumes Father etc Every attribute of a
etc.
concept is also present in the subsumed
concepts
R. Akerkar 13