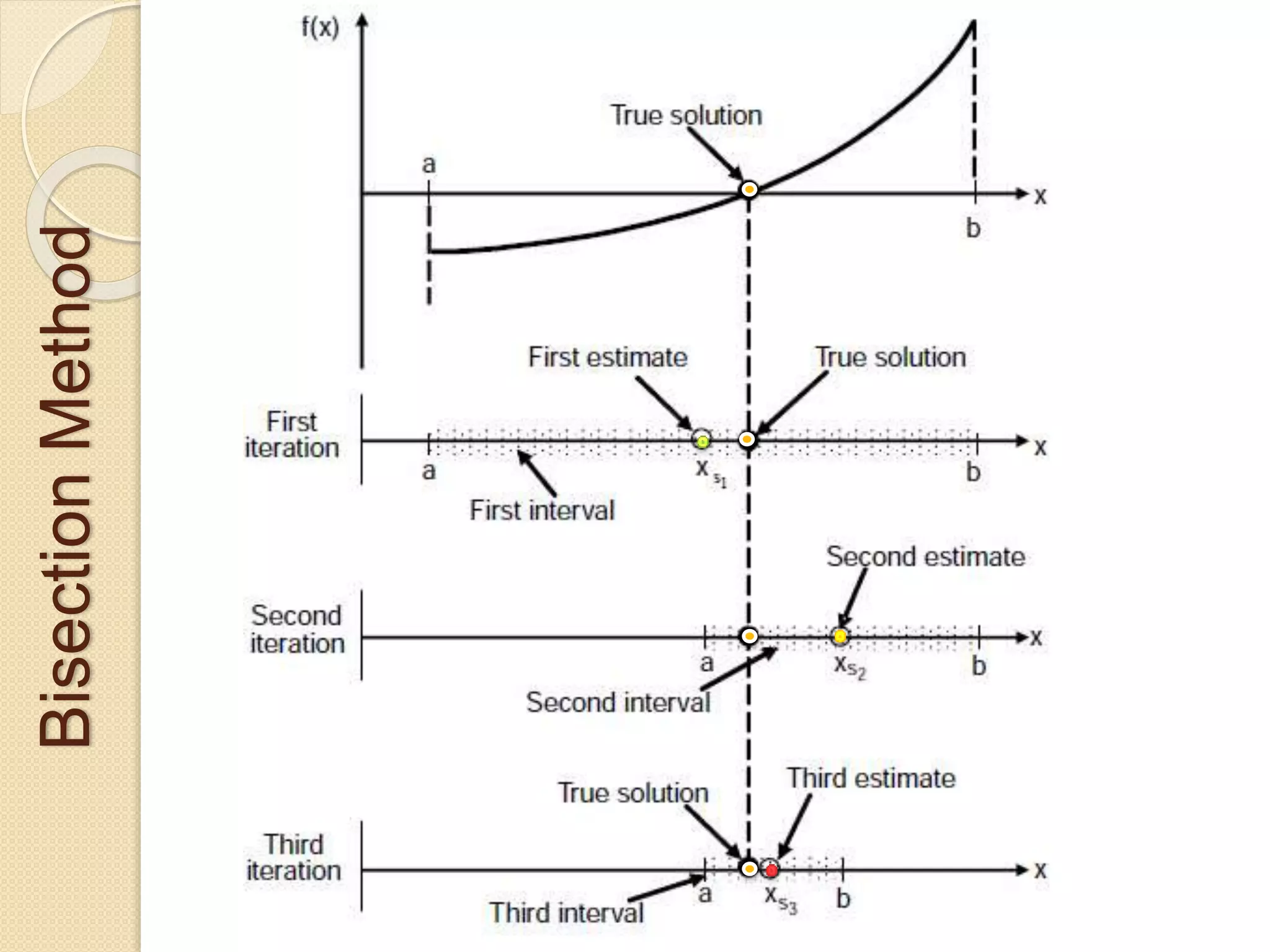
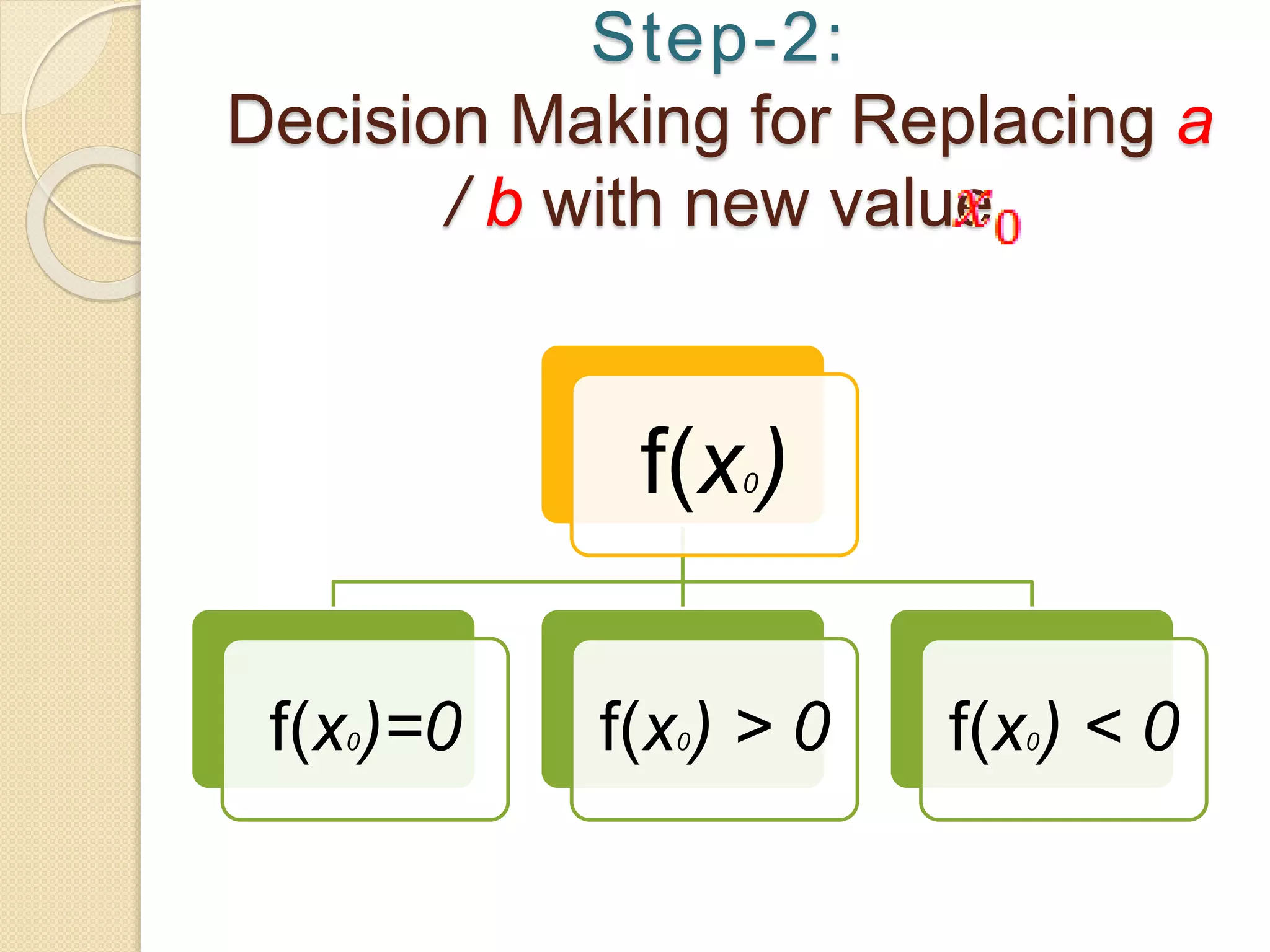
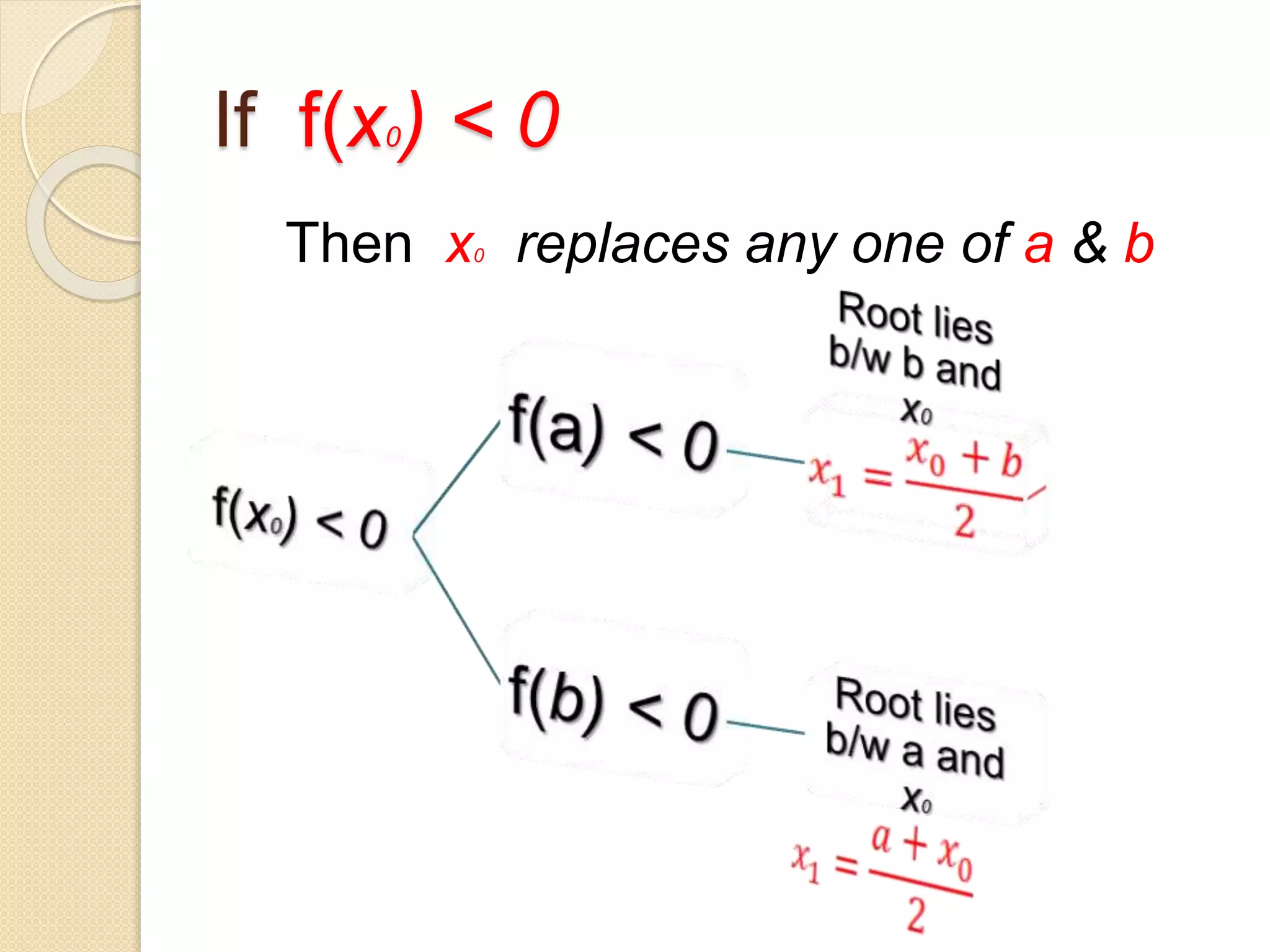
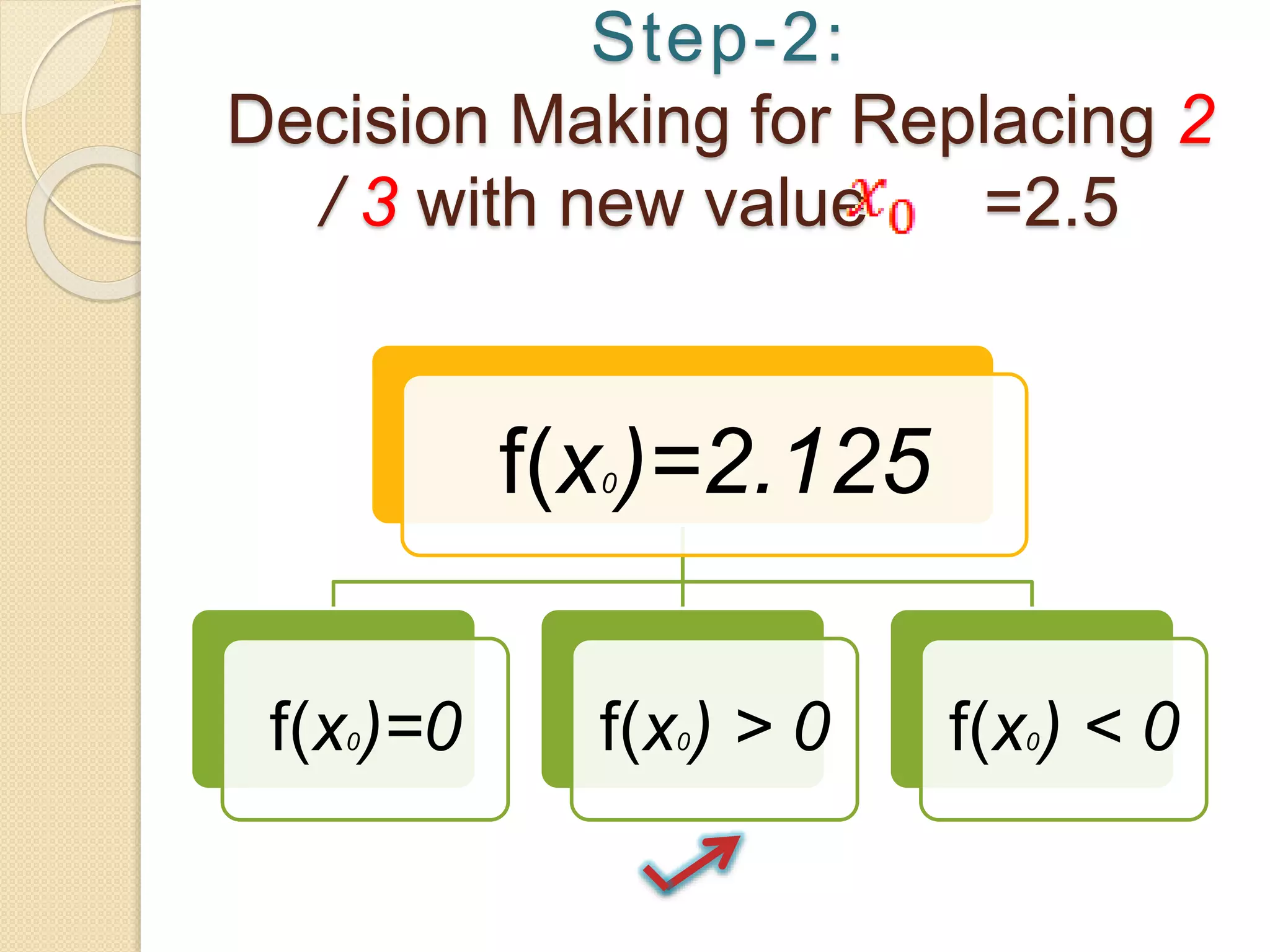
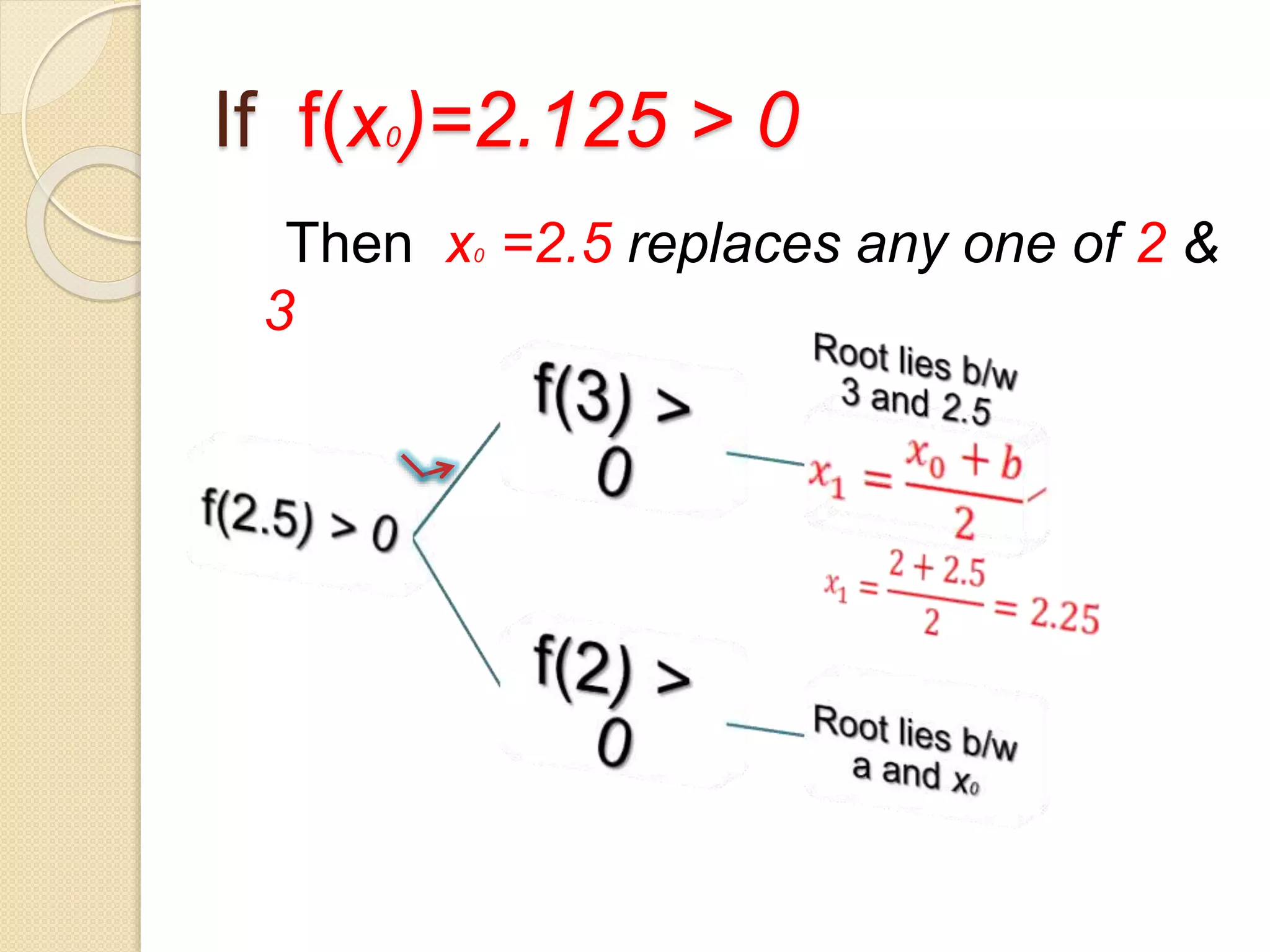
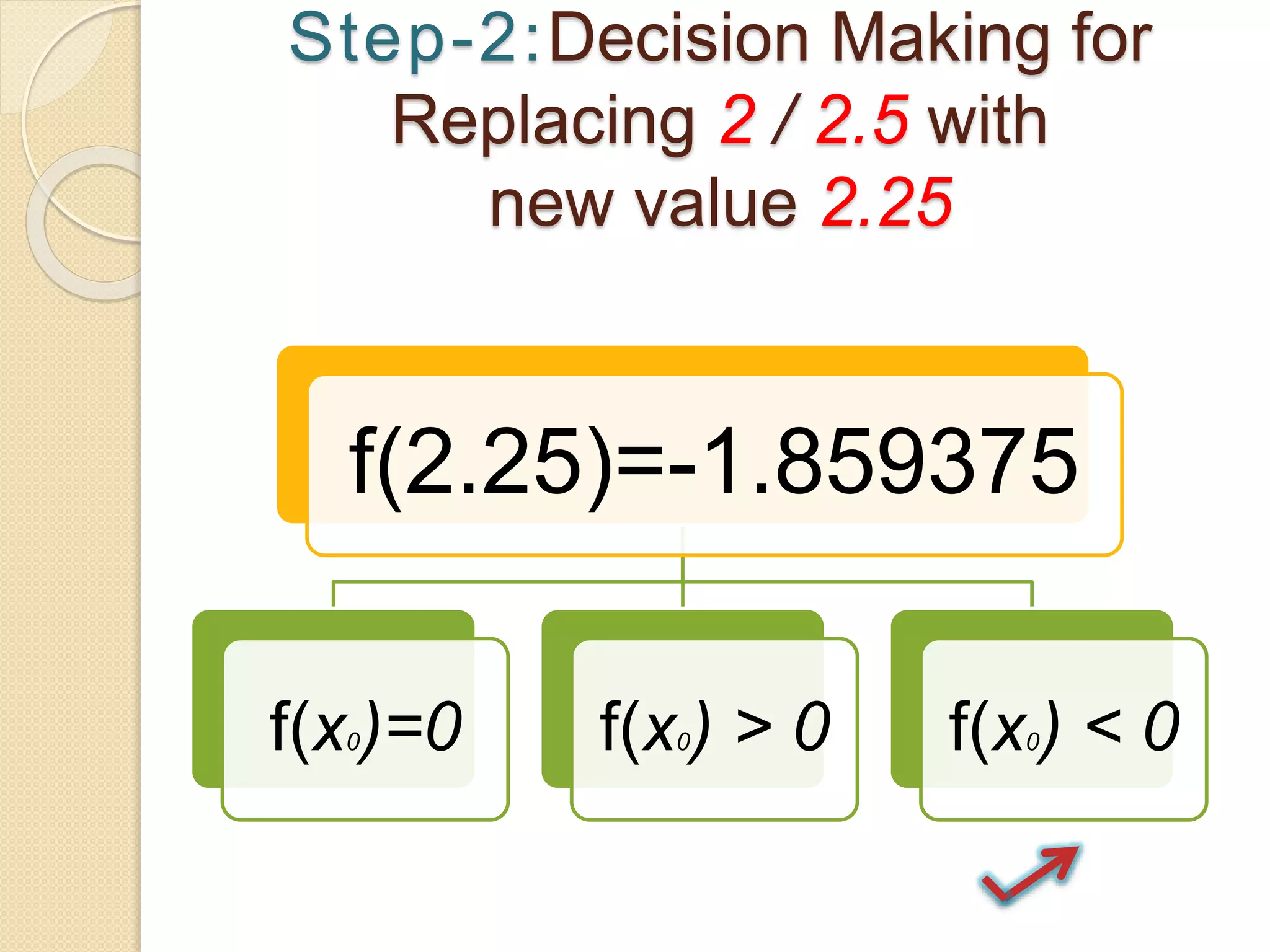
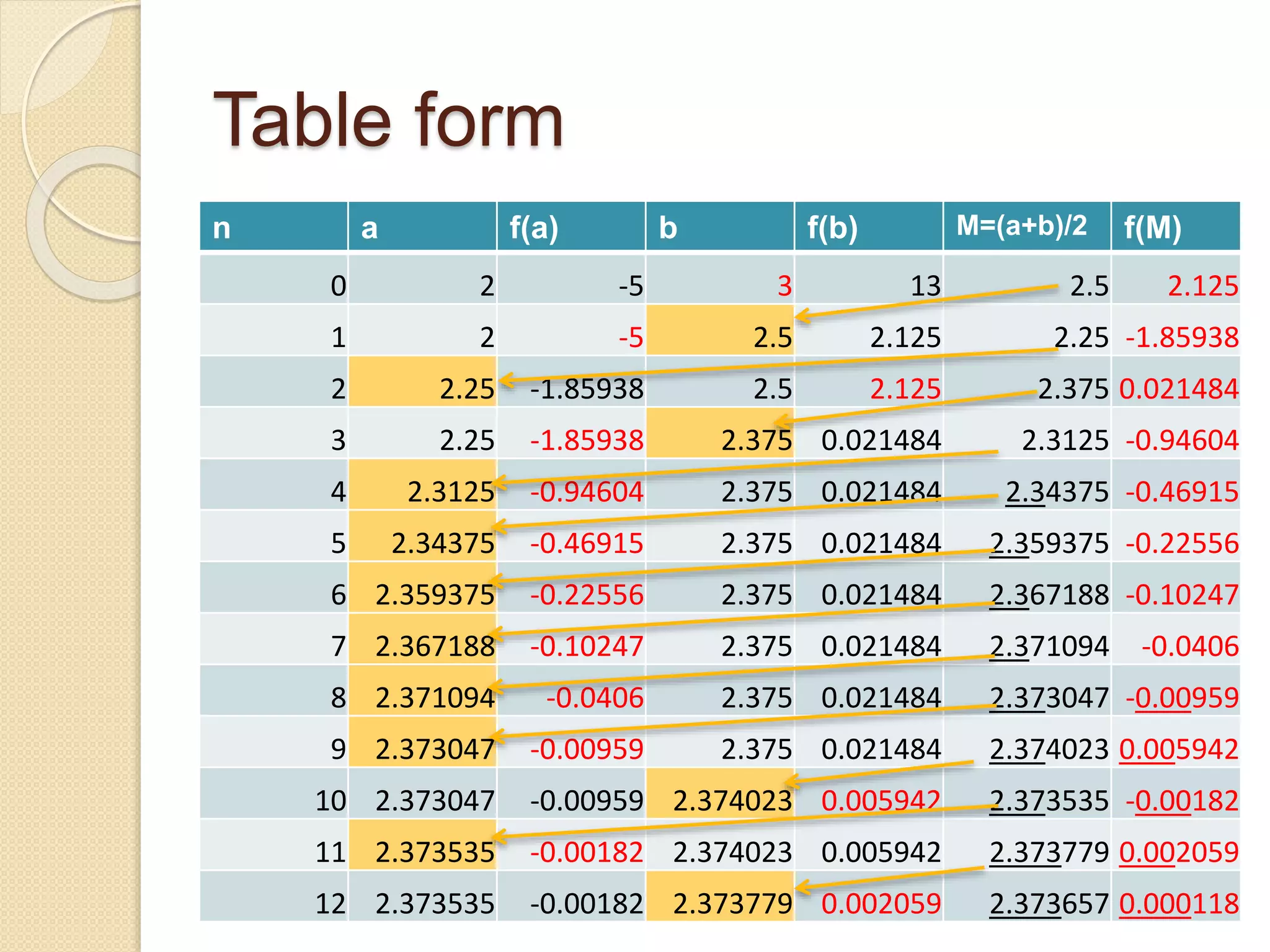
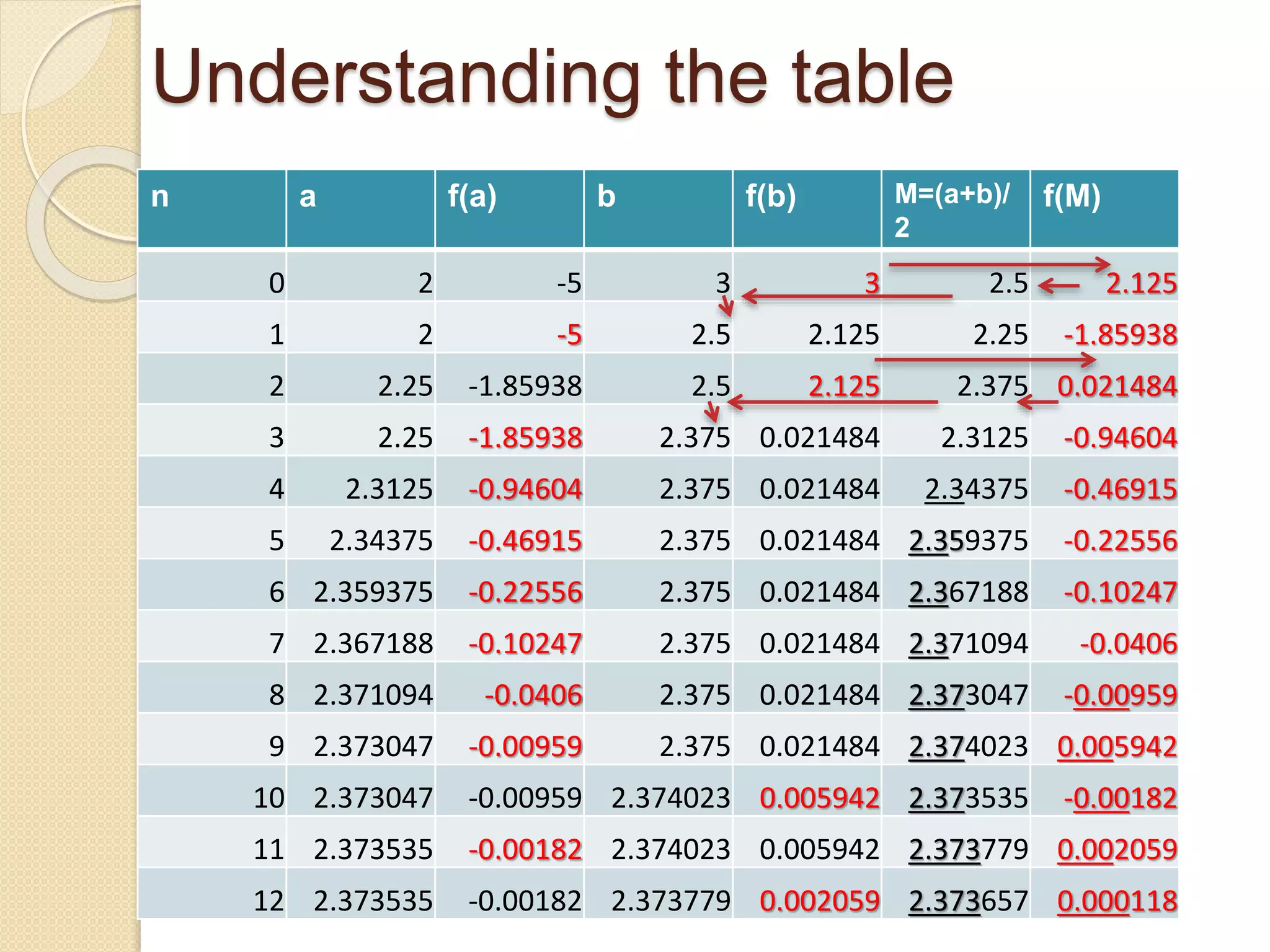
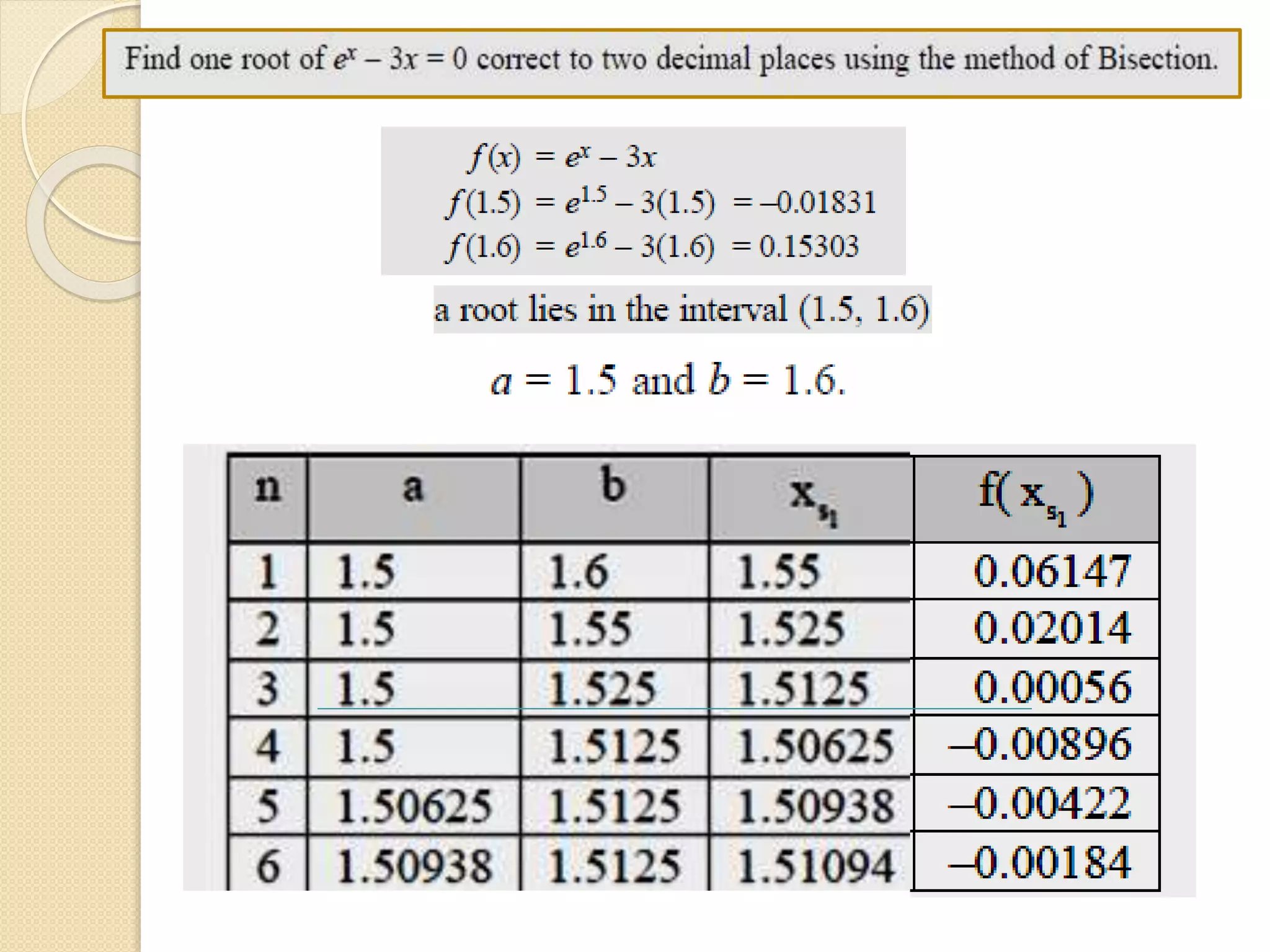
The document discusses the bisection method for finding real roots of equations. It provides the step-by-step algorithm for applying the bisection method. The key steps are: (1) find two values a and b where the function has opposite signs, (2) compute the midpoint x0 between a and b and evaluate the function there, (3) replace either a or b with x0 depending on whether f(x0) is positive or negative, and (4) repeat until the desired accuracy is reached. The document includes an example of applying the bisection method to find the root of the equation f(x) = x^3 - 2x - 5 between 2 and 3.

1. B.E. 4th Semester
Maths-IV: 140001
Numerical Analysis
Prof. K.K.Pokar
Assistant Professor in Mathematics
Government Engineering College,Bhuj

2. Numerical Methods
Bisection Method

3. Bisection Method

4. Bisection Method

5. BisectionMethod

6. Algorithm for Bisection Method
Step-1:
 Find the two points a and b
such that f(a) f(b) < 0
 Compute
 Evaluate

7. Step-2:
Decision Making for Replacing a
/ b with new value
f(x0)
f(x0)=0 f(x0) > 0 f(x0) < 0

8. If f(x0)=0
Then x0 is the required
root/solution
of the given equation
f(x) = 0

9. If f(x0) > 0
Then x0 replaces any one of a & b

10. If f(x0) < 0
Then x0 replaces any one of a & b

11. Step-3:
Repeating Step-2 for in place of
till the desired accuracy is obtained

12. Example: Find a real root of the
equation
 Step-1:
 Find the two points a and b such that f(a) f(b)
< 0
 Compute
 Evaluate

13. Step-2:
Decision Making for Replacing 2
/ 3 with new value =2.5
f(x0)=2.125
f(x0)=0 f(x0) > 0 f(x0) < 0

14. If f(x0)=2.125 > 0
Then x0 =2.5 replaces any one of 2 &
3

15. Step-2:Decision Making for
Replacing 2 / 2.5 with
new value 2.25
f(2.25)=-1.859375
f(x0)=0 f(x0) > 0 f(x0) < 0

16. If f(2.25) < 0
Then 2.25 replaces any one of 2 &
2.5
Root lies
b/w
2.25 and
2.5

17. Table form
n a f(a) b f(b) M=(a+b)/2 f(M)
0 2 -5 3 13 2.5 2.125
1 2 -5 2.5 2.125 2.25 -1.85938
2 2.25 -1.85938 2.5 2.125 2.375 0.021484
3 2.25 -1.85938 2.375 0.021484 2.3125 -0.94604
4 2.3125 -0.94604 2.375 0.021484 2.34375 -0.46915
5 2.34375 -0.46915 2.375 0.021484 2.359375 -0.22556
6 2.359375 -0.22556 2.375 0.021484 2.367188 -0.10247
7 2.367188 -0.10247 2.375 0.021484 2.371094 -0.0406
8 2.371094 -0.0406 2.375 0.021484 2.373047 -0.00959
9 2.373047 -0.00959 2.375 0.021484 2.374023 0.005942
10 2.373047 -0.00959 2.374023 0.005942 2.373535 -0.00182
11 2.373535 -0.00182 2.374023 0.005942 2.373779 0.002059
12 2.373535 -0.00182 2.373779 0.002059 2.373657 0.000118

18. Understanding the table
n a f(a) b f(b) M=(a+b)/
2
f(M)
0 2 -5 3 3 2.5 2.125
1 2 -5 2.5 2.125 2.25 -1.85938
2 2.25 -1.85938 2.5 2.125 2.375 0.021484
3 2.25 -1.85938 2.375 0.021484 2.3125 -0.94604
4 2.3125 -0.94604 2.375 0.021484 2.34375 -0.46915
5 2.34375 -0.46915 2.375 0.021484 2.359375 -0.22556
6 2.359375 -0.22556 2.375 0.021484 2.367188 -0.10247
7 2.367188 -0.10247 2.375 0.021484 2.371094 -0.0406
8 2.371094 -0.0406 2.375 0.021484 2.373047 -0.00959
9 2.373047 -0.00959 2.375 0.021484 2.374023 0.005942
10 2.373047 -0.00959 2.374023 0.005942 2.373535 -0.00182
11 2.373535 -0.00182 2.374023 0.005942 2.373779 0.002059
12 2.373535 -0.00182 2.373779 0.002059 2.373657 0.000118