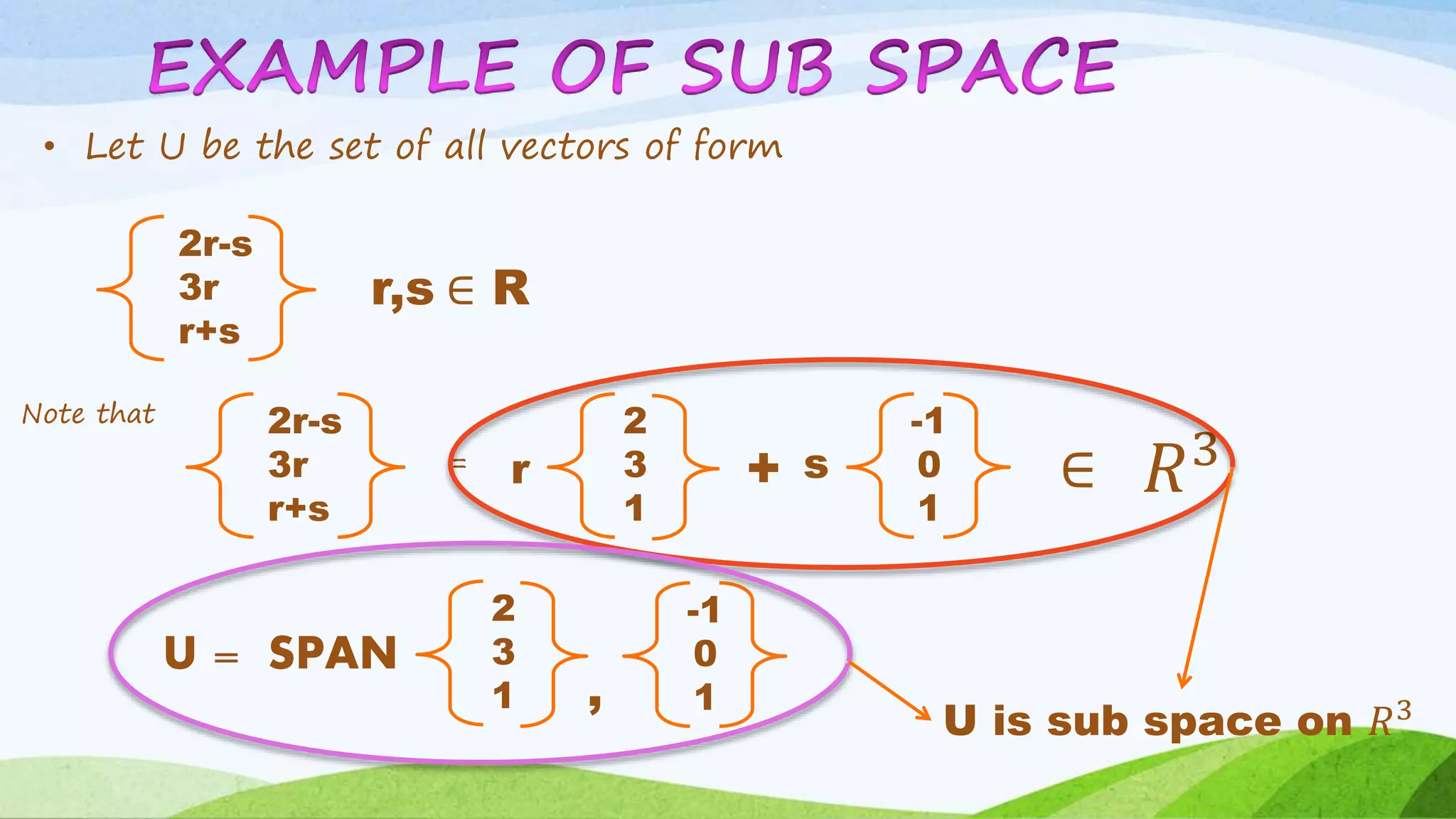
The document explains the concept of vector spaces and subspaces, detailing axioms related to vector addition and scalar multiplication. It outlines the criteria for a subset to be considered a subspace, such as closure under addition and scalar multiplication and the existence of a zero vector. Additionally, it provides examples and properties that validate these concepts in the context of real number spaces.

1. GOVERNMENT ENGINEERING COLLEGE
BHUJ

2. PRESENTED BY :-
150150113011
150150113012
150150113013
150150113014
150150113015
150150113016
150150113017
150150113018
150150113019
150150113020
SUBMITTED TO :-
PROF. K.K.POKAR

5. • A vector space is a nonempty set V
of objects, called vectors on which
are defined two operations, called
vector addition and scalar
multiplication.
DIDNT
UNDERSTAN
D ,LETS TRY
THIS .

6. 1. ADDITIVE AXIOMS
2. MULTIPAL AXIOMS
3. BELONGING AXIOMS

7. AXIOM 1
For every pair of element u and v in V
there corresponds a unique element in
V called the sum of u and v denoted by
Here V is set
and
U and v are
element

8. AXIOM 3
Commutative Law
For all u and v, we have

9. AXIOM 4
Associative Law
For all u and v, we have

10. AXIOM 5
Existence of Zero Element
There is an element in V denoted
by O such that

11. AXIOM 6
Existence of Negative
For every u in v, the element (-1)u
has the property

12. DEAD END!!!
CLICH HERE
TO GO BACK

13. AXIOM 2
For every u in V and every real
number k there corresponding's
an element in V called the
product k and u, denoted by ku.

14. AXIOM 7
Associate Law
For Every u in V and all real number
k and m, we have

15. AXIOM 8
Distributive Law For Addition
in V
For all u and v in V and all real k,
We have

16. AXIOM 9

17. AXIOM 10
Existence of Identity
For every u in V, We have

18. (1) AXIOM 1 (CLOSURE UNDER
ADDITION)
(2) AXIOM 2 (CLOSURE UNDER
MULTIPLICATION)
(3) AXIOM 5 (EXISTUNCE OF ZERO
ELEMENT)
(4) AXIOM 6 (EXISTENCE OF NEGATIVE )

19. • A subspace is a vector
space inside a vector space.
When we look at various
vector spaces, it is often
useful to examine their
subspaces.
FOR MORE
CLICK HERE

20. • The subspace S of a vector space V is that S is a subset of V
and that it has the following key characteristics
• S is closed under scalar multiplication: if λ∈R, v∈S, λv∈S
• S is closed under addition: if u, v ∈ S, u+v∈S.
• S contains 0, the zero vector.
• Any subset with these characteristics is a subspace.
PROPERTIES

22. Let V = 𝑅 𝑛 be the set
X = (𝑎1 + 𝑎2 +………….+ 𝑎 𝑛) ∈ 𝑅 𝑛
Y = (𝑏1 + 𝑏2 +………….+ 𝑏 𝑛) ∈ 𝑅 𝑛
we have to show that 𝑅 𝑛
is an vector space.

23. (1) Closure : -
Since X , Y ∈ 𝑅 𝑛
𝑎1, 𝑏2 ∈ R and hence
(𝑎1 + 𝑏2) ∈ R
Therefore X + Y ∈ R

24. Let X = (𝑎1 + 𝑎2 +………….+ 𝑎 𝑛) ∈ 𝑅 𝑛
Y = (𝑏1 + 𝑏2 +………….+ 𝑏 𝑛) ∈ 𝑅 𝑛
Z = (𝑐1 + 𝑐2 +………….+ 𝑐 𝑛) ∈ 𝑅 𝑛
(X+Y)+Z =((𝑎1 + 𝑏1)+𝑐1, (𝑎2+ 𝑏2)+𝑐2+……….+(𝑎 𝑛+ 𝑏 𝑛)+𝑐 𝑛)
=(𝑎1 + 𝑏1+𝑐1, 𝑎2 + 𝑏2+𝑐2+……….+𝑎 𝑛 + 𝑏 𝑛+𝑐 𝑛)
=(𝑎1 + (𝑏1+𝑐1), 𝑎2 +( 𝑏2+𝑐2)+……….+𝑎 𝑛 + (𝑏 𝑛+𝑐 𝑛))
= X+(Y+Z)
(2) Associative

25. (3)Existence of zero element
Here the zero vector 0 = (0,0,0,……,0)
Then for any X ∈ 𝑅 𝑛
X+O = (𝑎1 + 𝑎2 +………….+ 𝑎 𝑛) + (0,0,0,………,0)
= (𝑎1 + 0, 𝑎2 + 0, 𝑎3 + 0,…………. 𝑎 𝑛 + 0)
= (𝑎1 + 𝑎2 +………….+ 𝑎 𝑛) = X

26. (4)Existence of negative
Let X ∈ 𝑅 𝑛
then
(-1)X = -X is the additive inverse of X
Since –X = (-𝑎1,- 𝑎2,…………., -𝑎 𝑛)
X + (-1) = (𝑎1, 𝑎2,…………., 𝑎 𝑛) + (-𝑎1,- 𝑎2,…………., -𝑎 𝑛)
= (𝑎1 − 𝑎1, 𝑎2 − 𝑎2, 𝑎3 − 𝑎3,………….., 𝑎 𝑛 − 𝑎 𝑛)
= (0,0,0,………,0) = 0 –X + X

27. (5)Commutative Law
It follows from the commutative in R,
X + Y = Y + X
That’s
easy

28. (6)Distributive law of number
Let k ,m ∈ R, Then
(k + m)X = ((k + m) 𝑎1, (k + m) 𝑎2,…………, (k + m) 𝑎 𝑛)
= ( k𝑎1 + m𝑎1, k𝑎2 + m𝑎2,………., k𝑎 𝑛 + m𝑎 𝑛,)
=( k 𝑎1, k 𝑎2,…., k 𝑎 𝑛) + ( m 𝑎1, m 𝑎2,…., m 𝑎 𝑛)
= kX + mX

29. (7)Distributive Law for vector
addition
K ( X + Y ) = k((𝑎1 + 𝑎2 +……….+ 𝑎 𝑛) + (𝑏1 + 𝑏2 +………….+ 𝑏 𝑛))
=k(𝑎1 + 𝑏1, 𝑎2 + 𝑏2, 𝑎3 + 𝑏3,………….., 𝑎 𝑛 + 𝑏 𝑛)
= (k𝑎1 + k𝑎2 +…….+k 𝑎 𝑛) + (k𝑏1 + k𝑏2 +……+ 𝑘𝑏 𝑛)
= kX + kY
Remember k is
scalar quantity
where X and Y
are vector
quantity

30. (8)Existence of Identity
1 . X =1 . (𝑎1, 𝑎2,…………., 𝑎 𝑛)
= (𝑎1, 𝑎2,…………., 𝑎 𝑛)
= X

31. (9)Associative law for
multiplication of numbers
For ever x in 𝑅 𝑛 and all real numbers k and m ∈ 𝑅
(km)X = (km) (𝑎1, 𝑎2,…………., 𝑎 𝑛)
= (𝑘𝑚𝑎1, km𝑎2,…………., km𝑎 𝑛)
=k (𝑚𝑎1, m𝑎2,…………., m𝑎 𝑛)
=k(m (𝑎1, 𝑎2,…………., 𝑎 𝑛) )
=k(mX)

32. • Let U be the set of all vectors of form
2r-s
3r
r+s
r,s ∈ R
Note that 2r-s
3r
r+s
=
2
3
1
r +
-1
0
1
∈ 𝑅3
U = SPAN
2
3
1
-1
0
1,
U is sub space on 𝑅3
s

34. VECTOR = MAGNITUDE + DIRECTION
5 mph East
Speed
Scalar
Velocity = Vector
I am sure that you
got that

35. DEAD END!!!
CLICH HERE
TO GO BACK

37. DEAD END!!!
CLICH HERE
TO GO BACK

38. Plane y-z
Is a subspace

39. DEAD END!!!
CLICH HERE
TO GO BACK