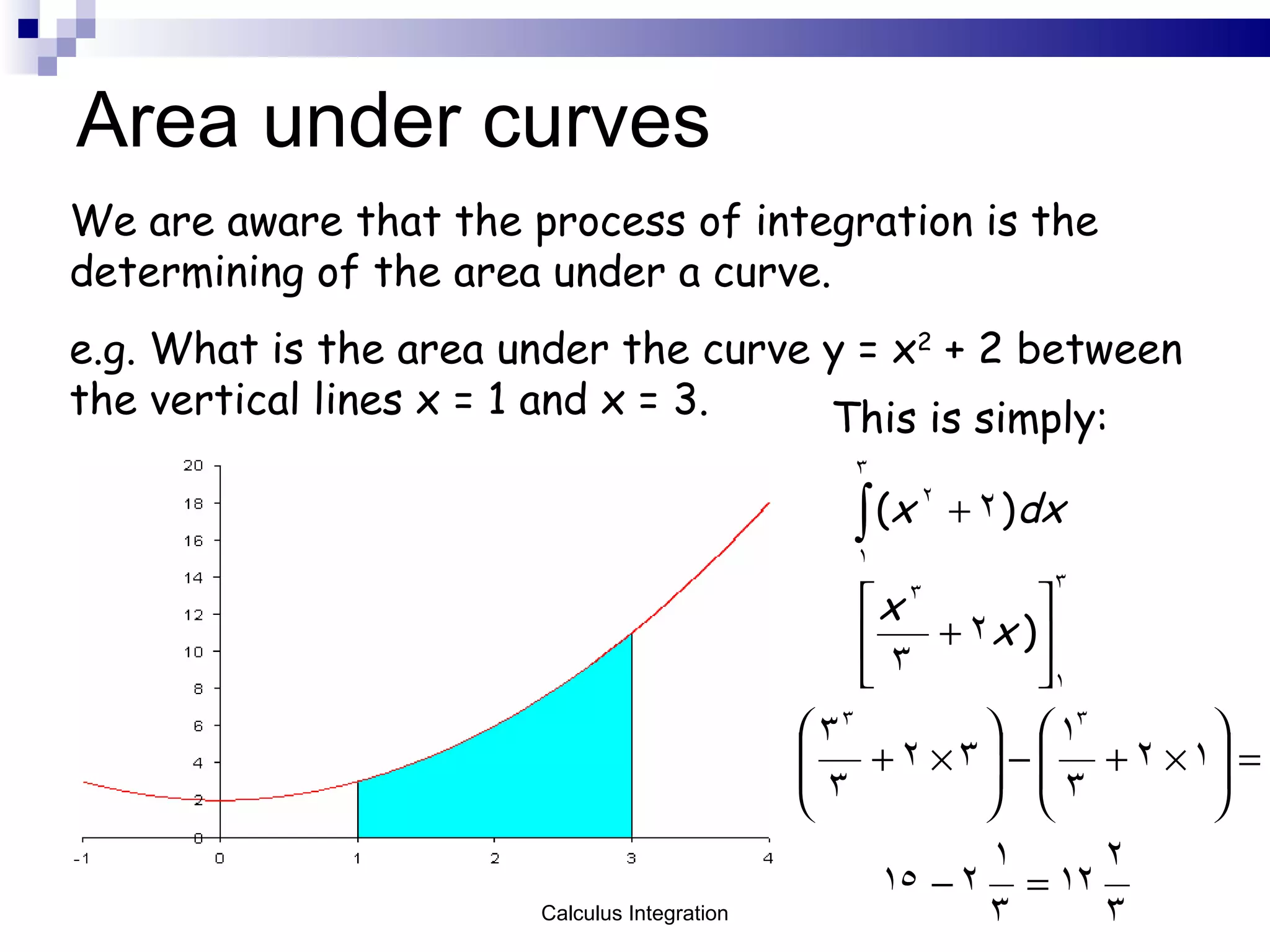
This document provides an introduction to integration (calculus) as taught in an undergraduate engineering course. It defines integration as the reverse process of differentiation and describes how it can be used to find the area under a curve. The document outlines key integration terminology like indefinite integrals, definite integrals, and the constant of integration. It also provides examples of integrating common functions and using integration to calculate volumes of solids of revolution.



![Terminology A definite integral is typically explained by the area problem as follows. Suppose we attempt to find the area of the region, S, under the curve y = (x) bounded from lower limit a to upper limit b , where is a continuous function. S x y (x) To estimate S, we divide the range [ a, b ] into n subintervals, that is, [ x 0 , x 1 ], [ x 1 , x 2 ], [ x 2 , x 3 ], . . . , [ x n− 1 , x n ], Each of width Δ x = ( b − a ) /n (so x i = a + i Δ x ). a b Calculus Integration](https://image.slidesharecdn.com/chapter4integration-100121074747-phpapp01/75/Chapter-4-Integration-4-2048.jpg)
![Terminology x y (x) b a x i-1 x i (x i *) The area S i of the strip between x i−1 and x i can be approximated as the rectangular area with width Δ x and height f(x i *), where x i * is a sample point in [x i-1 , x i ]. So the total area under the curve is approximated: which is called a Riemann Sum. Calculus Integration](https://image.slidesharecdn.com/chapter4integration-100121074747-phpapp01/75/Chapter-4-Integration-5-2048.jpg)













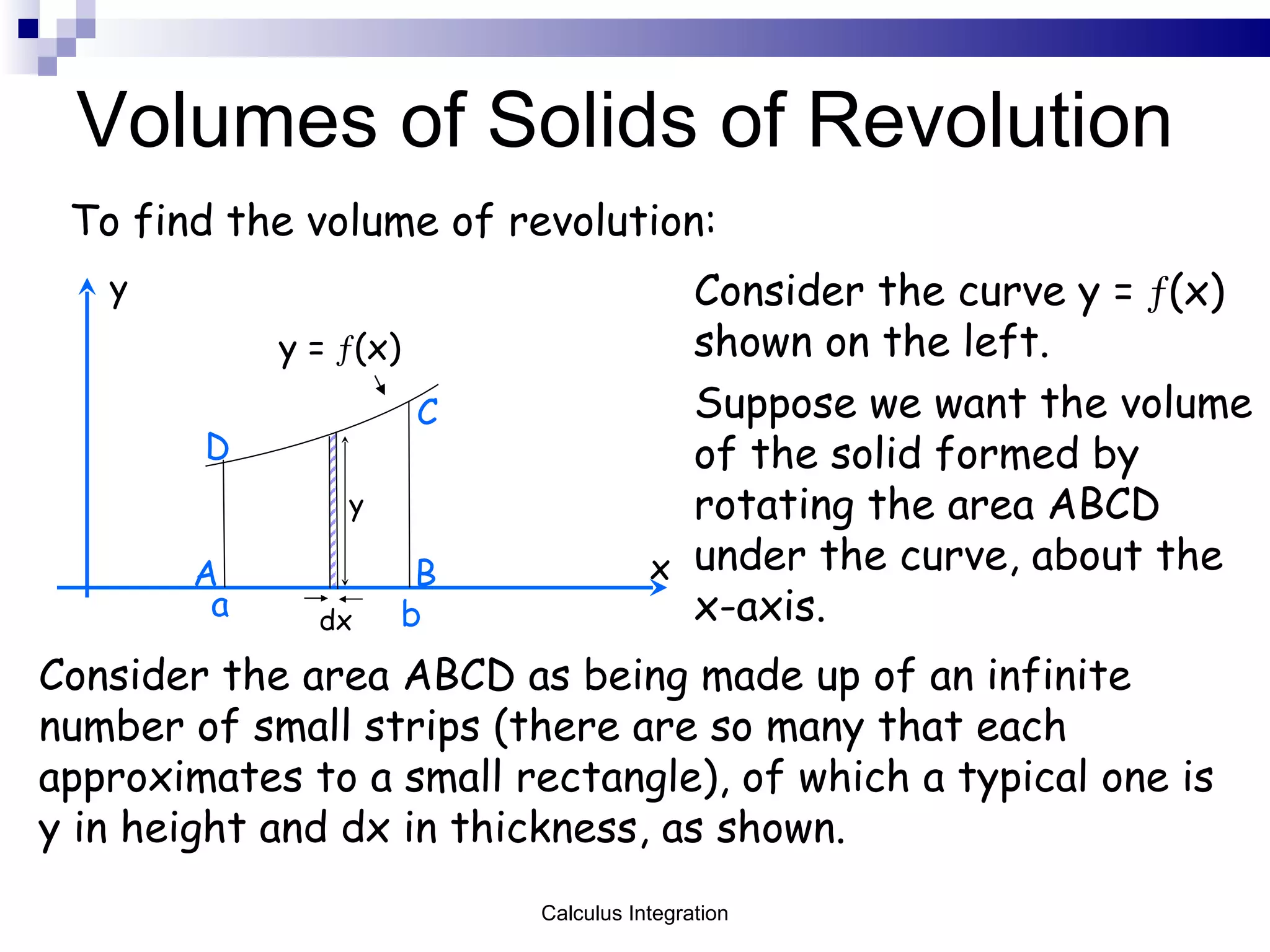
![Volumes of Solids of Revolution When rotated the rectangle of area = y dx becomes a cylinder of volume = π y 2 dx. [note volume of a cylinder = π r 2 h where r = y and h = dx] Thus the volume generated in rotating the area ABCD about the x-axis will be the sum of all these small cylindrical volumes, formed by rotating the area of strips about the x-axis from x = a to x = b. i.e. in calculus form N.B. substitute x in terms of y before you integrate](https://image.slidesharecdn.com/chapter4integration-100121074747-phpapp01/75/Chapter-4-Integration-21-2048.jpg)





![Examples The curve y = 2x 2 + 3 is rotated about the x-axis through 360 º, between the limits x = 1 and x = 3. Find the volume of the of the solid of rotation formed. [Ans = 991.5 units 3 ] 2. Find the volume of the solid obtained by rotating about the x-axis the part of the curve y = 2x 2 – 7x – 4 lying below the axis. [Ans = 772.9 units 3 ] Calculus Integration](https://image.slidesharecdn.com/chapter4integration-100121074747-phpapp01/75/Chapter-4-Integration-27-2048.jpg)
