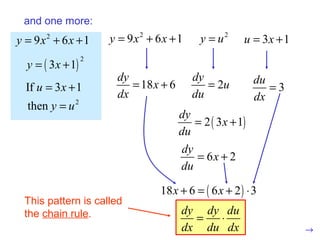
The document discusses the chain rule, which is used to find the derivative of composite functions. It provides examples of applying the chain rule to functions of the form f(g(x)) by taking the derivative of the outside function with respect to the inside function, and multiplying by the derivative of the inside function with respect to x. The chain rule can be used repeatedly when a function is composed of multiple nested functions. Derivative formulas themselves incorporate the chain rule. The chain rule is essential for finding derivatives and is the most common mistake made by students on tests.

1. Made by:
Rudra Patel
Harsh Desai
Ravi Patel
Rishabh Patel
Harshil Raymagiya

2. We now have a pretty good list of “shortcuts” to find
derivatives of simple functions.
Of course, many of the functions that we will encounter
are not so simple. What is needed is a way to combine
derivative rules to evaluate more complicated functions.
®

3. Consider a simple composite function:
y = 6x -10
y = 2( 3x -5)
If u = 3x -5
then y = 2u
y = 6x -10 y = 2u u = 3x - 5
= 2 dy
dy 6
dx
du
= du 3
dx
=
6 = 2×3
dy = dy ×
du
dx du dx
®

4. and another:
y = 5u - 2
where u = 3t
then y = 5( 3t ) - 2
u = 3t
dy 15
dt
= dy 5
du
= du 3
dt
=
15 = 5×3
dy = dy ×
du
dt du dt
y = 5( 3t ) - 2
y =15t - 2
y = 5u - 2
®

5. and one more:
y = 9x2 + 6x +1
( ) 2 y = 3x +1
If u = 3x +1
u = 3x +1
dy 18x 6
dx
y = u2
= + dy 2u
du
= du 3
dx
=
dy = dy ×
du
dx du dx
then y = u2
y = 9x2 + 6x +1
dy 2( 3x 1)
du
= +
dy = 6x +
2
du
18x + 6 = ( 6x + 2) ×3
This pattern is called
the chain rule.
®

6. dy dy du
dx du dx
Chain Rule: = ×
f o g y = f ( u) u = g ( x)
If is the composite of and ,
then:
o ¢ = ¢ × ¢
( ) at u g( x) at x f g f g =
example: f ( x) = sin x g ( x) = x2 - 4 Find: ( f o g )¢ at x = 2
f ¢( x) = cos x g¢( x) = 2x g ( 2) = 4 - 4 = 0
f ¢( 0) × g¢( 2)
cos ( 0) ×( 2×2)
1× 4 = 4
®

7. We could also do it this way:
f ( g ( x) ) = sin ( x2 - 4)
y = sin ( x2 - 4)
y = sin u u = x2 - 4
dy = cosu
du =
2x
du
dx
dy = dy ×
du
dx du dx
dy = cosu ×
2x
dx
dy = cos ( x2 - 4) ×
2x
dx
dy = cos ( 22 - 4) × 2 ×
2
dx
dy = cos( 0) ×
4
dx
dy =
4
dx
®

8. Here is a faster way to find the derivative:
y = sin ( x2 - 4)
y ¢ = cos( x2 - 4) ´ d ( x2 -
4)
dx
y¢ = cos ( x2 - 4) ´2x
Differentiate the outside function...
…then the inside function
At x = 2, y¢ = 4
®

9. Another example:
d cos2 ( 3x)
dx
d éë cos ( 3x
) 2 dx
ùû
2 cos ( 3x) d cos ( 3x)
dx
éë ùû ×
derivative of the
outside function
derivative of the
inside function
It looks like we need to
use the chain rule again!
®

10. Another example:
d cos2 ( 3x)
dx
d éë cos ( 3x
) 2 dx
ùû
2 cos ( 3x) d cos ( 3x)
dx
éë ùû ×
2cos ( 3x) sin ( 3x) d ( 3x)
dx
×- ×
-2cos ( 3x) ×sin ( 3x) ×3
-6cos ( 3x) sin ( 3x)
The chain rule can be used
more than once.
(That’s what makes the
“chain” in the “chain rule”!)
®

11. Derivative formulas include the chain rule!
d un = nun - 1 du
d sin u =
cosu du
dx dx
dx dx
d cosu sin u du
dx dx
= - d tan u =
sec2 u du
dx dx
etcetera…
The formulas on the memorization sheet are written with
instead of . Don’t forget to include the term!
u¢
du u¢
dx
®

12. The most common mistake on the chapter 3 test is to
forget to use the chain rule.
Every derivative problem could be thought of as a chain-rule
problem:
d x2
dx
2x d x
dx
= = 2x ×1 = 2x
derivative of
outside function
derivative of
inside function
The derivative of x is one.
®

13. The chain rule enables us to find the slope of
parametrically defined curves:
dy = dy ×
dx
dt dx dt
dy
dt dy
dx =
dx
dt
Divide both sides by
dx
The slope of a pardatmetrized
curve is given by:
dy
dy dt
dx dx
dt
=
®

14. Example: x = 3cos t y = 2sin t
These are the equations for
an ellipse.
dx 3sin t
dt
= - dy 2cos t
dt
dy t
dx t
= 2cos
=
-
3sin
2 cot
3
= - t

15. p