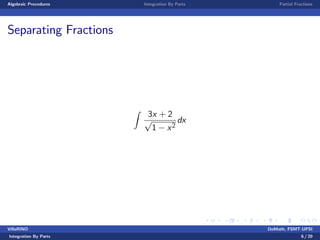
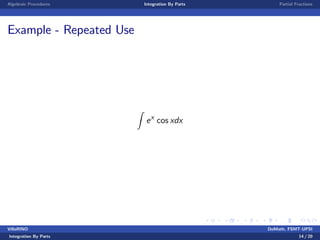
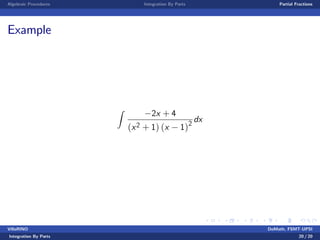
This document is a lecture on integration techniques including integration by parts and partial fractions. It introduces the formula for integration by parts and provides examples of applying the technique. It also explains the method of partial fractions for rewriting rational functions as a sum of simpler fractions and includes examples of using partial fractions. The goal is for students to learn how to apply techniques of integration like algebraic procedures, integration by parts, and partial fractions.

1. Beginning Calculus
- Integration By Parts -
Shahrizal Shamsuddin Norashiqin Mohd Idrus
Department of Mathematics,
FSMT - UPSI
(LECTURE SLIDES SERIES)
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 1 / 20

2. Algebraic Procedures Integration By Parts Partial Fractions
Learning Outcomes
Apply techniques of integration:
Algebraic procedures
Integration by parts
Partial fractions
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 2 / 20

3. Algebraic Procedures Integration By Parts Partial Fractions
Simplifying Substitution - Example
Z
2x 9
p
x2 9x + 1
dx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 3 / 20

4. Algebraic Procedures Integration By Parts Partial Fractions
Completing The Square - Example
Z
dx
p
8x x2
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 4 / 20

5. Algebraic Procedures Integration By Parts Partial Fractions
Reducing Improper Fraction - Example
Z
3x2 7x
3x + 2
dx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 5 / 20

6. Algebraic Procedures Integration By Parts Partial Fractions
Separating Fractions
Z
3x + 2
p
1 x2
dx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 6 / 20

7. Algebraic Procedures Integration By Parts Partial Fractions
The Formula
d
dx
(uv) = v
du
dx
+ u
dv
dx
d (uv) = vdu + udv
udv = d (uv) vdu
Z
udv = uv
Z
vdu
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 7 / 20

8. Algebraic Procedures Integration By Parts Partial Fractions
The Formula
Z
udv = uv
Z
vdu
R
udv is expressed in terms of
R
vdu
with a proper choice of u and v, the second integral
R
vdu may be
easier to evaluate.
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 8 / 20

9. Algebraic Procedures Integration By Parts Partial Fractions
Using IBP
WHEN:
if substitution does not work
HOW:
match
Z
f (x) g (x) dx with
Z
udv
u = f (x) , dv = g (x) dx or u = g (x) , dv = f (x) dx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 9 / 20

10. Algebraic Procedures Integration By Parts Partial Fractions
Example
Z
x cos xdx
Choice 1: u = 1, dv = x cos xdx
Choice 2: u = x, dv = cos xdx
Choice 3: u = x cos x, dv = dx
Choice 4: u = cos x.dv = xdx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 10 / 20

11. Algebraic Procedures Integration By Parts Partial Fractions
Example - continue
Choice 2:
u = x ) du = dx
dv = cos xdx ) v = sin x
Z
udv = uv
Z
vdu
)
Z
x cos xdx = x sin x
Z
sin xdx
= x sin x + cos x + C
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 11 / 20

12. Algebraic Procedures Integration By Parts Partial Fractions
Example
Z
ln xdx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 12 / 20

13. Algebraic Procedures Integration By Parts Partial Fractions
Example - Repeated Use
Z
x2
ex
dx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 13 / 20

14. Algebraic Procedures Integration By Parts Partial Fractions
Example - Repeated Use
Z
ex
cos xdx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 14 / 20

15. Algebraic Procedures Integration By Parts Partial Fractions
Partial Fractions
The method of rewriting rational functions as sum of simpler fractions is
called the method of partial fractions.
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 15 / 20

16. Algebraic Procedures Integration By Parts Partial Fractions
Two Distinct Linear Factors - Example
5x 3
x2 2x 3
=
A
x + 1
+
B
x 3
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 16 / 20

17. Algebraic Procedures Integration By Parts Partial Fractions
A Repeated Linear Factor - Example
6x + 7
(x + 2)2
=
A
x + 2
+
B
(x + 2)2
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 17 / 20

18. Algebraic Procedures Integration By Parts Partial Fractions
An Improper Fraction - Example
2x3 4x2 x 3
x2 2x 3
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 18 / 20

19. Algebraic Procedures Integration By Parts Partial Fractions
An Irreducible Quadratic Factor - Example
2x + 4
(x2 + 1) (x 1)2
=
Ax + B
x2 + 1
+
C
x 1
+
D
(x 1)2
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 19 / 20

20. Algebraic Procedures Integration By Parts Partial Fractions
Example
Z
2x + 4
(x2 + 1) (x 1)2
dx
VillaRINO DoMath, FSMT-UPSI
Integration By Parts 20 / 20