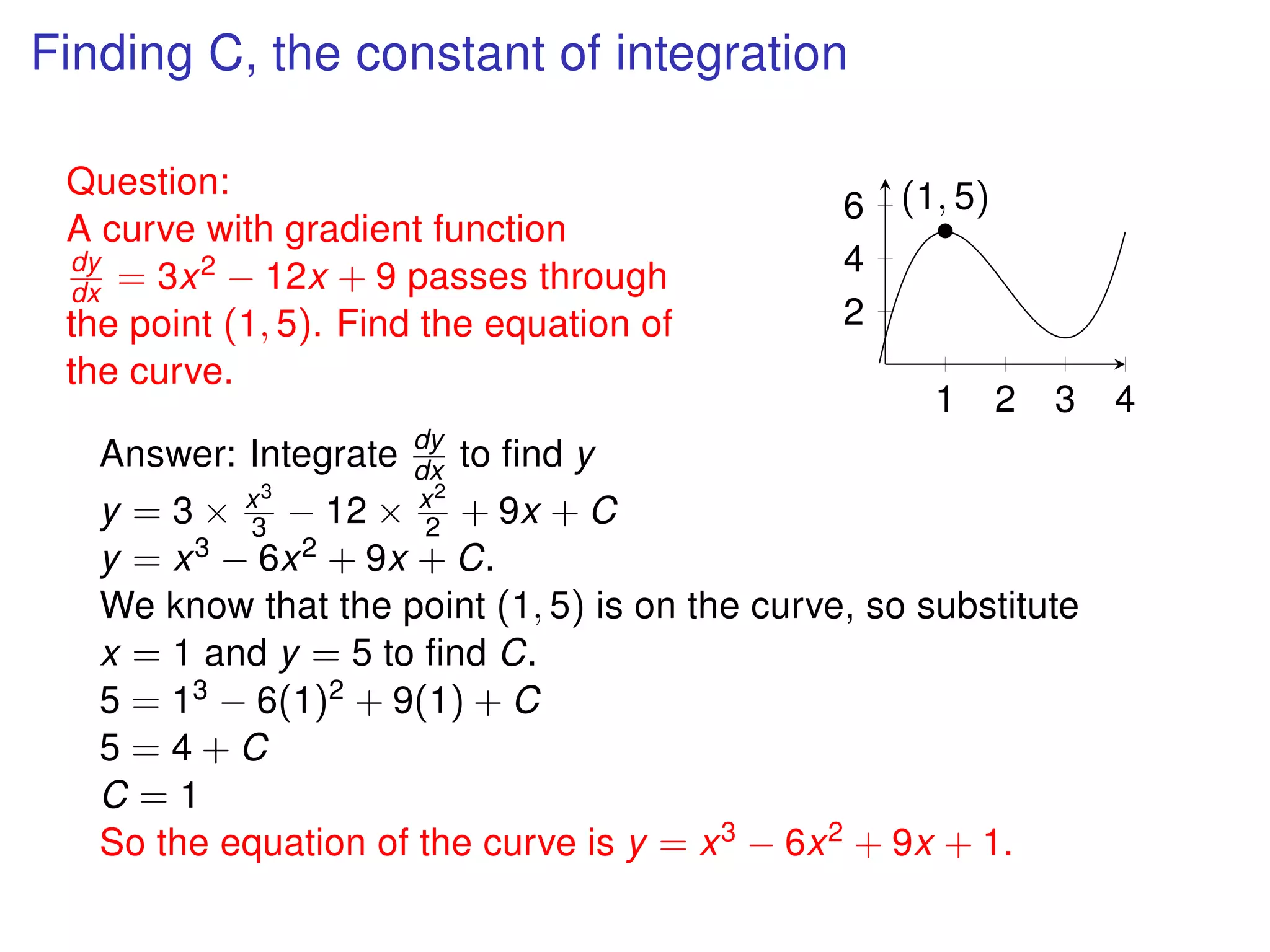
The document discusses integration, which is the reverse process of differentiation. It provides formulas for integrating polynomial expressions like xn and axn and explains how to find the constant of integration C. Examples are given for integrating expressions and finding the area under a curve by integrating between limits of integration.

1. Lecture 6 - Integration
C2 Foundation Mathematics (Standard Track)
Dr Linda Stringer Dr Simon Craik
l.stringer@uea.ac.uk s.craik@uea.ac.uk
INTO City/UEA London

2. Lecture 6 skills
integrate a polynomial expression
integrate the gradient function (dy
dx ) of a curve
find C, the constant of integration
integrate to find the area under a curve

3. Differentiation
If y = xn, then
dy
dx
= nxn−1
If y = x3 + x2 + x + 1, then
dy
dx
= 3x2
+ 2x + 1
If y = 2x3 + 5x2 + 7x + 200, then
dy
dx
= 6x2
+ 10x + 7
If y = x3
3 + x2
2 + x + 52, then
dy
dx
= x2
+ x + 1

4. The reverse of differentiation
Question: If dy
dx = 2x, what is y?
Answer: y = x2 + C?
Question: If dy
dx = 3x2, what is y?
Answer: y = x3 + C?
Question: If dy
dx = x2, what is y?
Answer: y = x3
3 + C?

5. Integration is the reverse of differentiation
If dy
dx = xn, then
y =
xn+1
n + 1
+ C, n = 1
C is called the constant of integration
If dy
dx = x5, then
y =
x5+1
5 + 1
+ C =
x6
6
+ C
If dy
dx = x2, then
y =
x3
3
+ C
If dy
dx = 3x2, then
y = 3 ×
x3
3
+ C = x3
+ C

6. Integration
Integration is the reverse of differentiation.
If we are given dy
dx , we integrate to find y.
We also use integration to find the area under a curve.
The integral of a function f(x) with respect to x is written as
f(x) dx

7. Integrating a polynomial
Let x be a variable, and a, b, n, m be constants
xn
dx =
xn+1
n + 1
+ C
axn
dx = a xn
dx =
axn+1
n + 1
+ C
axn
+ bxm
dx =
axn+1
n + 1
+
bxm+1
m + 1
+ C
Note: these formulae work for all n, m except for
n, m = −1.
Say ’the integral of xn, dx, is x to the n plus 1, over n plus
1, plus C.’

8. Examples
xn
dx =
xn+1
n + 1
+ C
What is the integral of x4 + x3 + x2 with respect to x?
Answer:
x4
+ x3
+ x2
dx =
x5
5
+
x4
4
+
x3
3
+ C
What is the integral of x2 + x + 1 with respect to x?
Answer:
x2
+ x + 1 dx =
x3
3
+
x2
2
+ x + C.

9. Examples
axn
dx =
axn+1
n + 1
+ C
What is the integral of 5x4 + 4x3 + 3x2 with respect to x?
Answer:
5x4
+4x3
+3x2
dx =
5x5
5
+
4x4
4
+
3x3
3
+C = x5
+x4
+x3
+C
What is the integral of 3x2 + 2x + 1 with respect to x?
Answer:
3x2
+ 2x + 1 dx =
3x3
3
+
2x2
2
+ x + C = x3
+ x2
+ x + C

10. Examples
axn
dx =
axn+1
n + 1
+ C
What is the integral of 2x−3 + 5 with respect to x?
Answer:
2x−3
+ 5 dx =
2x−2
−2
+ 5x + C = −x−2
+ 5x + C
What is the integral of 6x
1
2 with respect to x?
Answer:
6x
1
2 dx =
6x1/2+1
1/2 + 1
+C =
6x3/2
3/2
+C = 6x
3/2
×
2
3
+C =
4x3/2
3
+C

11. The same question asked in three ways
Question 1: If dy
dx = x6 + 10x + 3, what is y?
Question 2: Integrate x6 + 10x + 3 with respect to x.
Question 3: Find x6 + 10x + 3 dx.
Answer 1: y = x7
7 + 5x2 + 3x + C
Answer 2: x7
7 + 5x2 + 3x + C
Answer 3: x7
7 + 5x2 + 3x + C

12. Finding C, the constant of integration
Question:
A curve with gradient function
dy
dx = 3x2 − 12x + 9 passes through
the point (1, 5). Find the equation of
the curve.
1 2 3 4
2
4
6
•
(1, 5)
Answer: Integrate dy
dx to find y
y = 3 × x3
3 − 12 × x2
2 + 9x + C
y = x3 − 6x2 + 9x + C.
We know that the point (1, 5) is on the curve, so substitute
x = 1 and y = 5 to find C.
5 = 13 − 6(1)2 + 9(1) + C
5 = 4 + C
C = 1
So the equation of the curve is y = x3 − 6x2 + 9x + 1.

13. Finding C, the constant of integration
Question:
A line with gradient dy
dx = 6 passes
through the point (1, 5). Find the
equation of the line.
−2 2 4 6 8−2
2
4
6
8
•(1, 5)
Answer: Integrate dy
dx to find y
y = 6x + C
We know that the point (1, 5) is on the curve, so substitute
x = 1 and y = 5 to find C.
5 = 6 × 1 + C
C = −1
So the equation of the line is y = 6x − 1.

14. Use integration to finding the area under a curve
b
a
f(x) dx
is area under the curve y = f(x) between x = a and x = b.
a b
x
y
a and b are the limits of integration
a is the lower limit and b is the upper limit
is the integral sign (introduced by Leibniz in 1675)

15. The Fundamental Theorem of Calculus Part II
If f(x) dx = F(x), then
b
a
f(x) dx = [F(x)]b
a = [F(b)] − [F(a)]

16. Example
Question:
What is the area under the
curve y = 3x3 + 2 between
x = 0 and x = 2?
−1 1 2
10
20
30
Answer:
2
0 3x3 + 2 dx = [3x4
4 + 2x]2
0
= [3×(2)4
4 + 2 × 2] − [3×04
4 + 2 × 0]
= [12 + 4] − [0 + 0]
= [16] − [0] = 16

17. Example 2
Question:
What is the area under the
curve y = 6x2 + 2x−3 between
x = −2 and x = −1?
−2 −1
10
20
Answer:
−1
−2 6x2 + 2x−3 dx = [2x3 − x−2]−1
−2
= [2(−1)3 − (−1)−2] − [2(−2)3 − (−2)−2]
= [−2 − 1] − [−16 − 1
4 ]
= [−3] − [−64−1
4 ]
= 53
4 = 131
4 = 13.25

18. Differentiating and integrating - summary
Differentiate to find the derivative
If y = xn
, then
dy
dx
= nxn−1
Integrate to find the integral
xn
dx =
xn+1
n + 1
+ C If
dy
dx
= xn
, then y =
xn+1
n + 1
+ C
Differentiate








y = ax2 + bx + c
dy
dx = 2ax + b
d2y
dx2 = 2a








Integrate
Differentiate








y = ax3 + bx2 + cx + d
dy
dx = 3ax2 + 2bx + c
d2y
dx2 = 6ax + 2b








Integrate