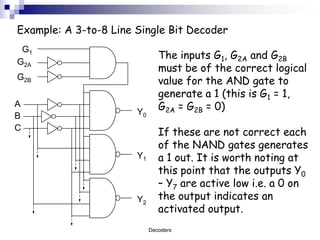
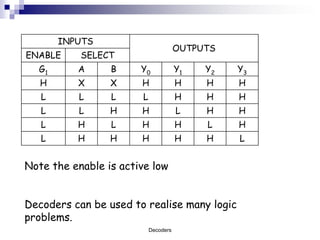
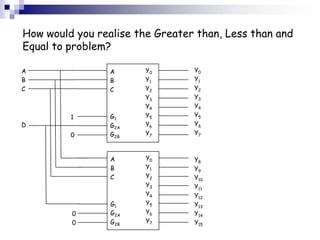
This document presents educational resources on digital logic and decoders as part of the University of Wales Newport's engineering courses. It covers concepts of decoders, including pin arrangements, truth tables, and practical examples in creating logic circuits using NAND gates. The resource aims to provide knowledge and skills relevant to contemporary engineering environments and is licensed under a Creative Commons Attribution 2.0 license.

1. Decoders
Digital Logic and Software
Applications
Level 4
© University of Wales Newport 2009 This work is licensed under a Creative Commons Attribution 2.0 License.

2. The following presentation is a part of the level 4 module -- Digital Logic and Signal Principles. This resources is a part of the 2009/2010
Engineering (foundation degree, BEng and HN) courses from University of Wales Newport (course codes H101, H691, H620, HH37 and 001H).
This resource is a part of the core modules for the full time 1st year undergraduate programme.
The BEng & Foundation Degrees and HNC/D in Engineering are designed to meet the needs of employers by placing the emphasis on the
theoretical, practical and vocational aspects of engineering within the workplace and beyond. Engineering is becoming more high profile, and
therefore more in demand as a skill set, in today’s high-tech world. This course has been designed to provide you with knowledge, skills and
practical experience encountered in everyday engineering environments.
Contents
 Decoder
 Pin Arrangement & Truth Table
 Example Diagrams
 Credits
In addition to the resource below, there are supporting documents which should be used in combination with this
resource. Please see:
 Holdsworth B, Digital Logic Design, Newnes 2002
 Crisp J, Introduction to Digital Systems, Newnes 2001
Decoders

3. Decoder
For a general description of decoder, please refer to
http://en.wikipedia.org/wiki/Decoder
Decoders

4. Example: A 3-to-8 Line Single Bit Decoder
G1
The inputs G1, G2A and G2B
G2A
must be of the correct logical
G2B value for the AND gate to
generate a 1 (this is G1 = 1,
A
Y0
G2A = G2B = 0)
B
C
If these are not correct each
of the NAND gates generates
Y1 a 1 out. It is worth noting at
this point that the outputs Y0
– Y7 are active low i.e. a 0 on
Y2 the output indicates an
activated output.
Decoders

5. The 8 NAND gates now have all eight combinations of the
three inputs A, B and C.
The Y0 NAND has not A, not B and not C so when A = B = C
= 0 then Y0 = 0 as long as the G inputs are of the correct
logic levels.
The other NANDs have other combinations – Y2 not A, B
and not C (010) and this would make Y2 = 0.
The integrated circuit that performs this function is a
74LS138.
Similar to this is the 74LS139 which contains 2 two to
four line decodes which work in a similar way. These have a
G1 input only and this must be at logic 0 for the outputs to
be activated.
Decoders

6. Pin Arrangement & Truth Table 74138
http://upgrade.kongju.ac.kr/data/ttl/74138.html
Decoders

7. Pin Arrangement 74139
http://upgrade.kongju.ac.kr/data/ttl/74139.html
Decoders

8. INPUTS
OUTPUTS
ENABLE SELECT
G1 A B Y0 Y1 Y2 Y3
H X X H H H H
L L L L H H H
L L H H L H H
L H L H H L H
L H H H H H L
Note the enable is active low
Decoders can be used to realise many logic
problems.
Decoders

9. Example
Three judges A, B and C vote: 1 guilty and 0 not guilty.
Design a logic circuit using NAND only which will allow a
majority decision (F) to be found. e.g. A = 1, B = 0, C = 0
gives an output of 0 (not guilty)
Output when
inputs are
A A Y0
B B Y1 011, 101, 110, 111
C C Y2
Y3
Y4
1 G1 Y5
0 G2A Y6
0 G2B Y7
NAND is used as we have
active low outputs

10. A 4-to-16 line decoder can be constructed in the
following way:
A A Y0 Y0
B B Y1 Y1
C C Y2 Y2
Y3 Y3
Y4 Y4
1 G1 Y5 Y5
D G2A Y6 Y6
0 G2B Y7 Y7
A Y0 Y8
B Y1 Y9
C Y2 Y10
Y3 Y11
Y4 Y12
G1 Y5 Y13
0 G2A Y6 Y14
0 G2B Y7 Y15
Decoders

11. How would you realise the Greater than, Less than and
Equal to problem?
A A Y0 Y0
B B Y1 Y1
C C Y2 Y2
Y3 Y3
Y4 Y4
1 G1 Y5 Y5
D G2A Y6 Y6
0 G2B Y7 Y7
A Y0 Y8
B Y1 Y9
C Y2 Y10
Y3 Y11
Y4 Y12
G1 Y5 Y13
0 G2A Y6 Y14
0 G2B Y7 Y15

12. This resource was created by the University of Wales Newport and released as an open educational resource
through the Open Engineering Resources project of the HE Academy Engineering Subject Centre. The Open
Engineering Resources project was funded by HEFCE and part of the JISC/HE Academy UKOER programme.
© 2009 University of Wales Newport
This work is licensed under a Creative Commons Attribution 2.0 License.
The JISC logo is licensed under the terms of the Creative Commons Attribution-Non-Commercial-No Derivative Works 2.0 UK: England &
Wales Licence. All reproductions must comply with the terms of that licence.
The HEA logo is owned by the Higher Education Academy Limited may be freely distributed and copied for educational purposes only,
provided that appropriate acknowledgement is given to the Higher Education Academy as the copyright holder and original publisher.
The name and logo of University of Wales Newport is a trade mark and all rights in it are reserved. The name and logo should not be
reproduced without the express authorisation of the University.
Decoders