The document discusses the concept and applications of definite integrals, illustrating how they are used to calculate areas under curves, volumes of solids of revolution, and other real-life applications in fields such as engineering, physics, and statistics. It explains methods for finding areas and volumes, including the disc and shell methods, and highlights the importance of calculus in various professional contexts. Examples include the application of integrals in architecture, electrical engineering, and medical science for tasks such as material estimation and growth rate analysis.

1. BY-
1) DEBANKA KHAN(29) 2) CHAYAN PATHAK(26)
3) DEBAJYOTI ROY CHOWDHURY(27) 4)DIGANTA GHOSH(32)

2. INDEX
1] INTRODUCTION
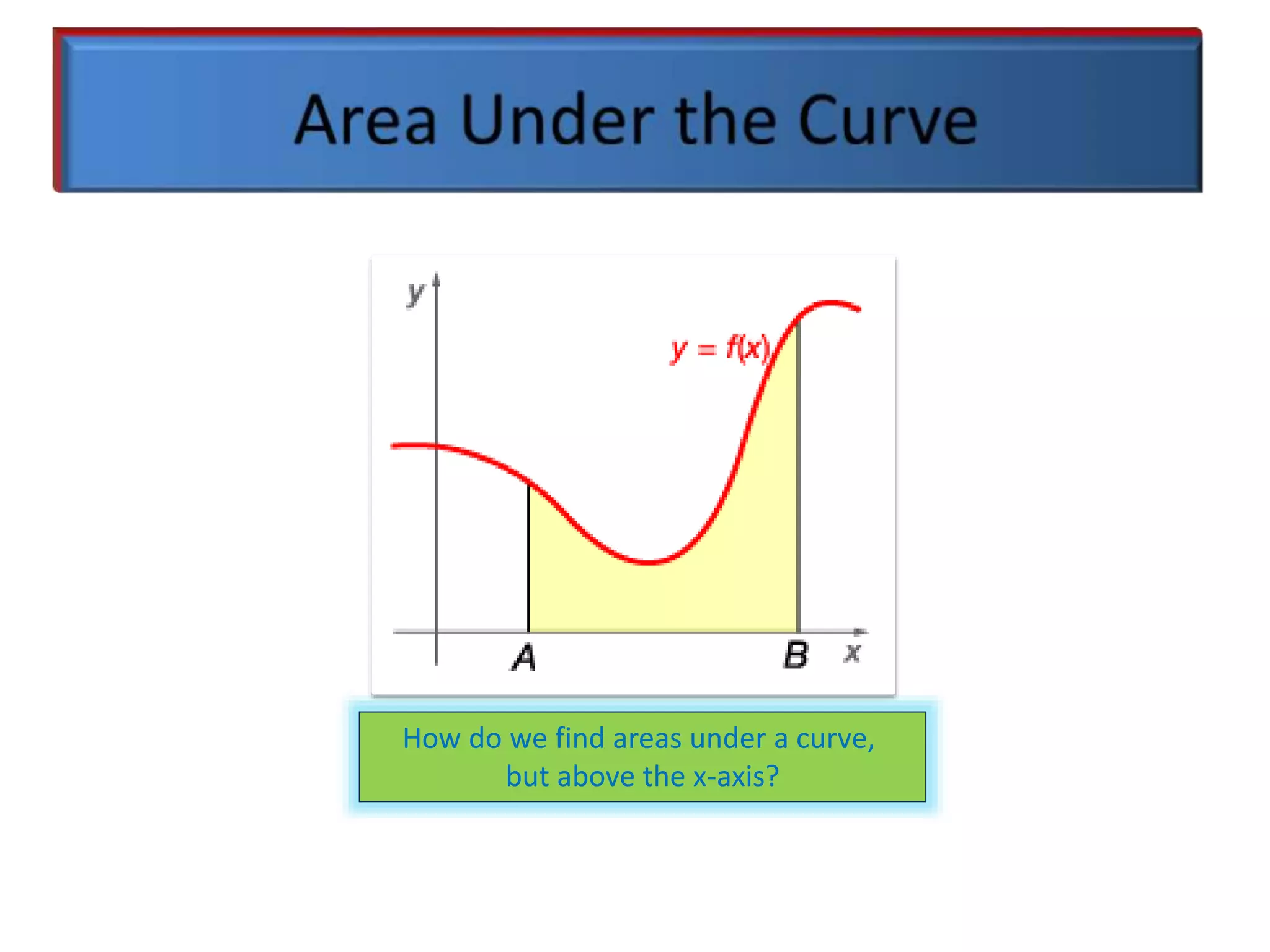
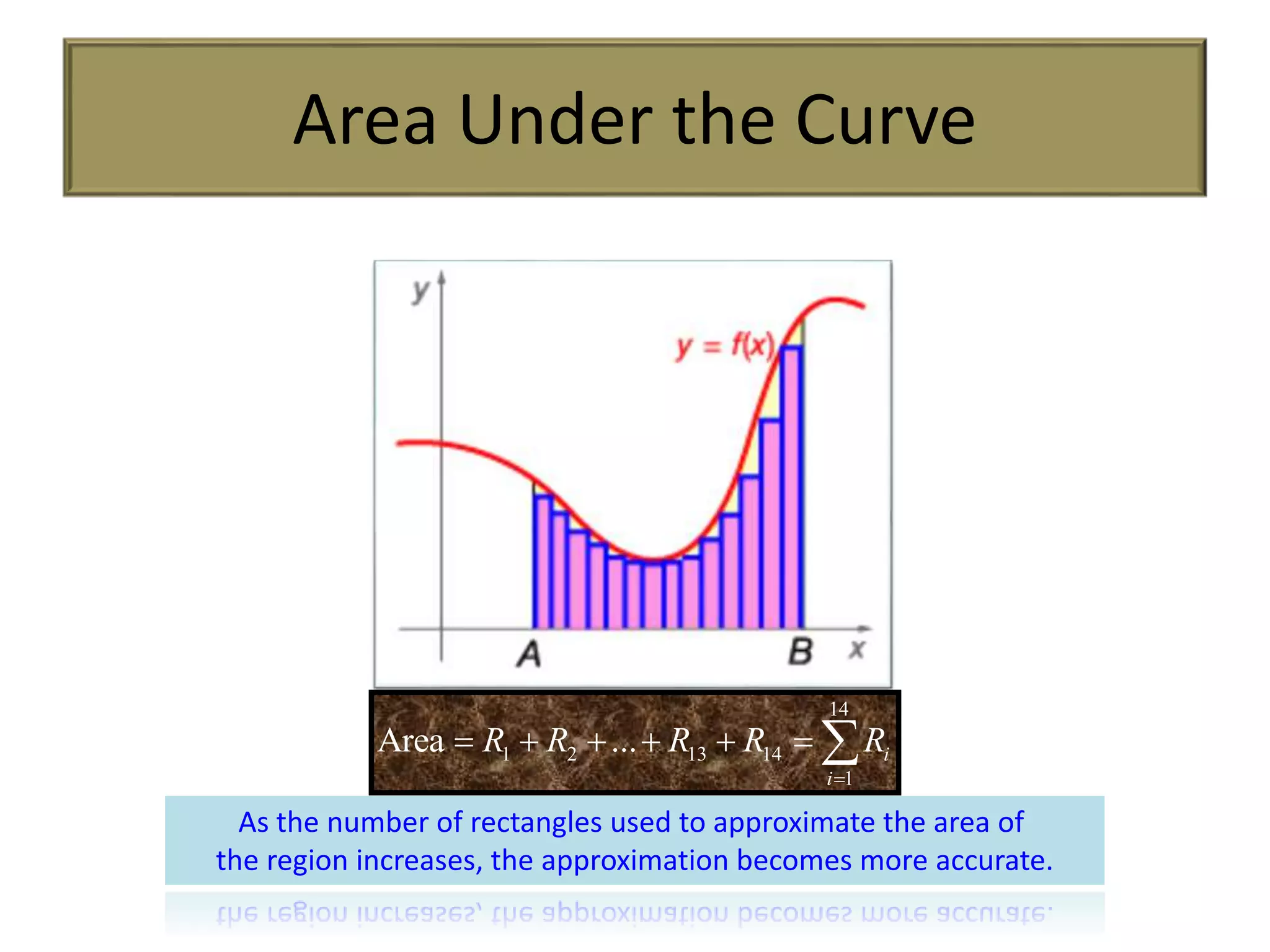
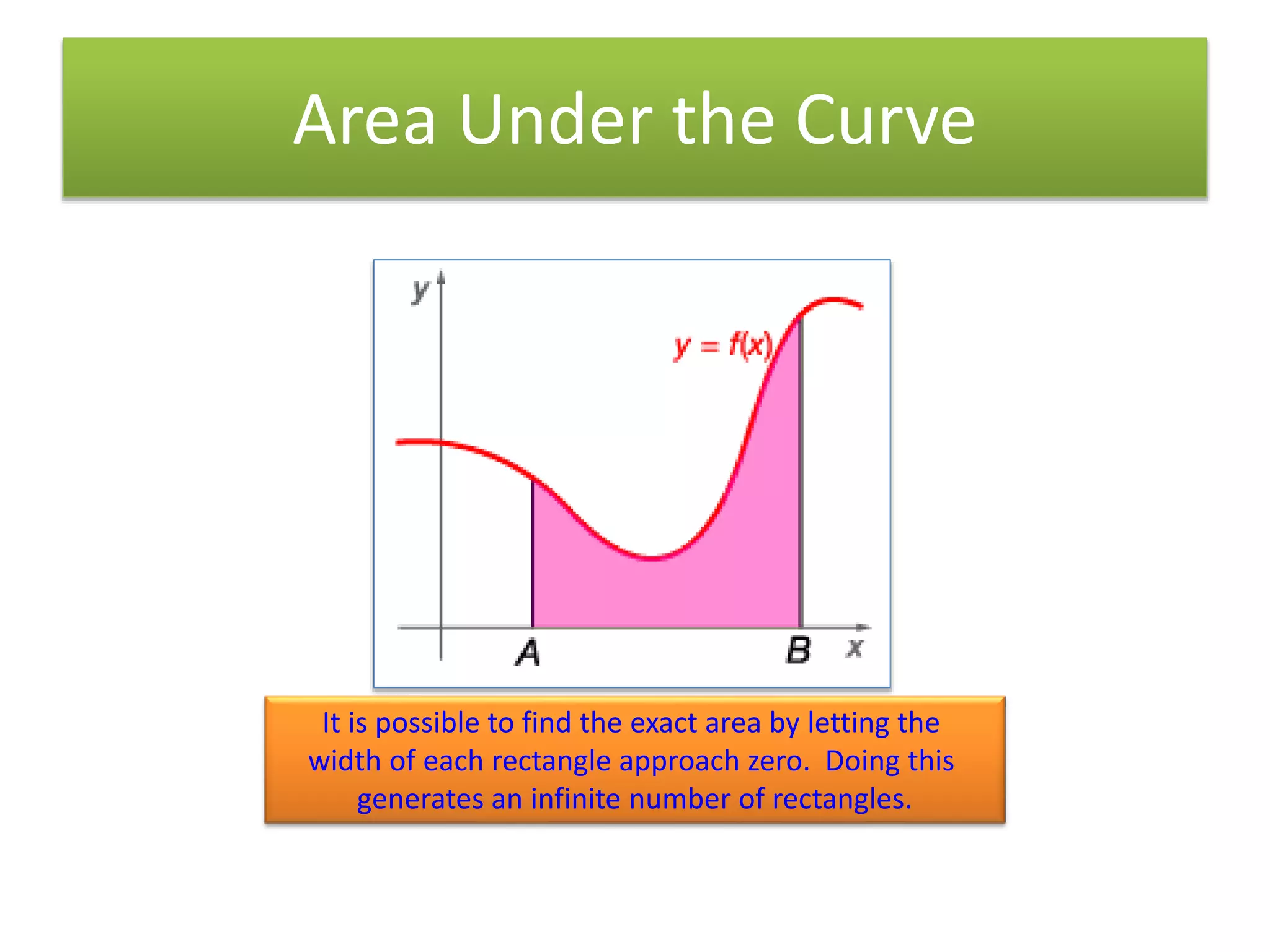
2]DETERMINATION OF AREA UNDER
THE CURVE
3]FINDING VOLUME OF REVOLUTION
4] APPLICATION OF DEFINITE INTEGRAL
IN VARIOUS OTHER FIELDS

3. INTRODUCTION
Definite intigral is used to calculate areas between two curves,
volumes, length of curves, and several other applications from
real life such as calculating the work done by a force, the pressure
a liquid exerts on an object, and basic statistical concept.
Definite intigral is an integral expressed as the difference between
the values of the integral at specified upper and lower limits of the
independent variable.
The major advance in integration came in the 17th century with
the independent discovery of the fundamental theorem of
calculus by Leibniz and Newton.

4. How do we find areas under a curve,
but above the x-axis?

5. Area Under the Curve
14
1 2 13 14
1
Area ... i
i
R R R R R

      
As the number of rectangles used to approximate the area of
the region increases, the approximation becomes more accurate.

6. Area Under the Curve
It is possible to find the exact area by letting the
width of each rectangle approach zero. Doing this
generates an infinite number of rectangles.

7. AN EXAMPLE OF CALCULATING AREA UNDER
THE CURVE USING DEFINITE INTIGRAL
  2
Consider f x x

Find the area between
the graph of f and the
x-axis on the interval
[0, 1].
1
2
0
Area x dx
 
3
3
x

0
1
 
1
3
  
0
3

2
1
3
Area units


8. FINDING VOLUME OF REVOLUTION
Two common methods for finding
the volume of a solid of
revolution are the disc method
and the shell method of
integration. To apply these
methods, it is easiest to draw the
graph in question; identify the
area that is to be revolved about
the axis of revolution; determine
the volume of either a disc-
shaped slice of the solid, with
thickness δx, or a cylindrical shell
of width δx; and then find the
limiting sum of these volumes as
δx approaches 0, a value which
may be found by evaluating a
suitable integral.

9. FINDING THE VOLUME OF REVOLUTION
USING DISC METHOD
The disk method is used when the slice that
was drawn is perpendicular to the axis
of revolution; i.e. when integrating
parallel to the axis of revolution.
The volume of the solid formed by rotating
the area between the curves of f(x) and
g(x) and the lines x = a and x = b about
the x-axis is given by
V= a∫b │ƒ(x)2 –g(x)2 │dx
If g(x)=0(e.g. revolving an area between the
curve and the X- axis), this reduces to:
V=  a∫b ƒ(x) 2 dx.

10. FINDING VOLUME OF REVOLUTION USING
CYLINDER METHOD
• The cylinder method is used when the
slice that was drawn is parallel to the axis
of revolution; i.e. when integrating
perpendicular to the axis of revolution.
• The volume of the solid formed by
rotating the area between the curves of
f(x) and g(x) and the lines x = a and x = b
about the y-axis is given by
V=2 a∫b x│ƒ(x) –g(x)│dx
If g(x)=0(e.g. revolving an area between the
curve and the y- axis), this reduces to:
V= 2 a∫b x│ƒ(x) │ dx.

11. APPLICATION OF DEFINITE INTEGRAL IN
VARIOUS OTHER FIELDS
APPLCATION IN ENGINEERING:.
1:An Architect Engineer uses integration in determining the amount of the
necessary materials to construct curved shape constructions (e.g. dome over a
sports arena) and also to measure the weight of that structure. Calculus is used to
improve the architecture not only of buildings but also of important
infrastructures such as bridges.
2:In Electrical Engineering, Calculus (Integration) is used to determine the exact
length of power cable needed to connect two substations, which are miles away
from each other.
3:Space flight engineers frequently use calculus when planning for long missions.
To launch an exploratory probe, they must consider the different orbiting
velocities of the Earth and the planet the probe is targeted for, as well as other
gravitational influences like the sun and the moon.

12. 2) In determination of cardiac output
APPLICATION IN MEDICAL SCIENCE:
1)Biologists use differential calculus to determine the exact rate
of growth in a bacterial culture when different variables such as
temperature and food source are changed.

13. • APPLICATION IN PHYSICS:
• 1) In Physics, Integration is very much needed. For example,
to calculate the Centre of Mass, Centre of Gravity and Mass
Moment of Inertia of a sports utility vehicle.
• 2)To calculate the velocity and trajectory of an object, predict
the position of planets, and understand electromagnetism.
• Application in Statistics:
• 1)Statisticians use calculus to evaluate survey data to help
develop business plans for different companies. Because a
survey involves many different questions with a range of
possible answers, calculus allows a more accurate prediction
for the appropriate action.

14. • Application in Research Analysis:
• An operations research analyst will use calculus when observing
different processes at a manufacturing corporation. By considering
the value of different variables, they can help a company improve
operating efficiency, increase production, and raise profits.
• Application in Graphics:
• A graphics artist uses calculus to determine how different three-
dimensional models will behave when subjected to rapidly
changing conditions. It can create a realistic environment for
movies or video games.
• Application in Chemistry:
• It is used to determine the rate of a chemical reaction and to
determine some necessary information of Radioactive decay
reactio