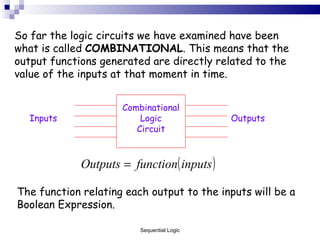
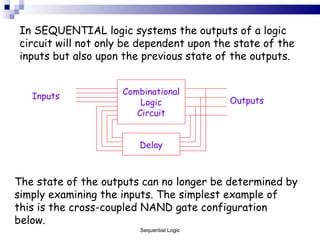
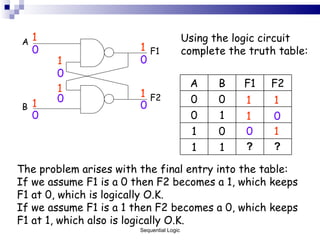
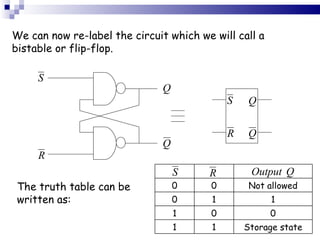
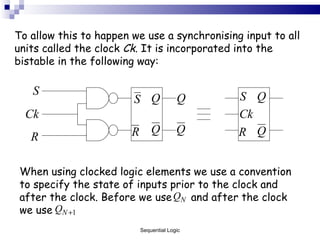
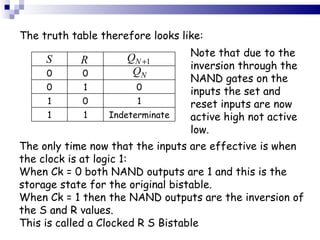
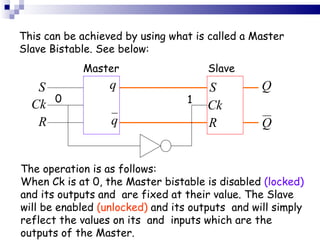
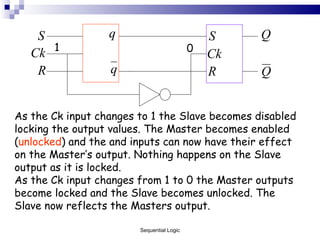
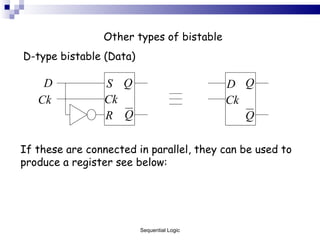
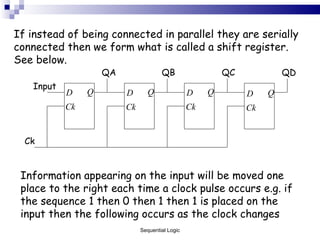
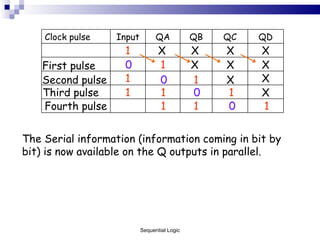
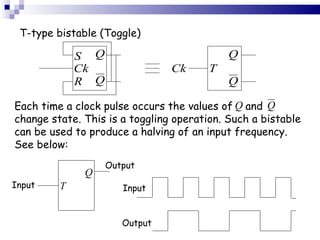
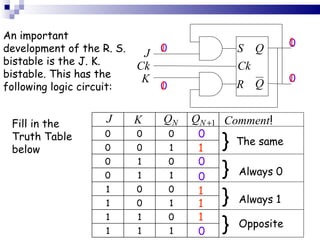
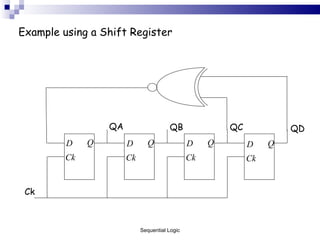
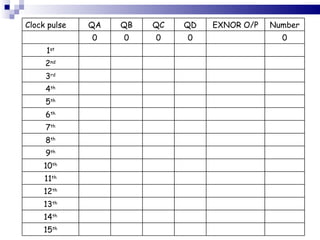
The document outlines sequential logic systems as part of the digital logic and signal principles module at the University of Wales Newport. It highlights the importance of sequential logic in engineering, detailing components like bistable circuits and their applications in digital systems, such as storage elements and registers. The material serves as an educational resource for developing practical skills in sequential logic and its implementation in engineering contexts.

1. Sequential Logic Digital Logic and Software Principles © University of Wales Newport 2009 This work is licensed under a Creative Commons Attribution 2.0 License .

2. The following presentation is a part of the level 4 module -- Digital Logic and Signal Principles. This resources is a part of the 2009/2010 Engineering (foundation degree, BEng and HN) courses from University of Wales Newport (course codes H101, H691, H620, HH37 and 001H). This resource is a part of the core modules for the full time 1 st year undergraduate programme. The BEng & Foundation Degrees and HNC/D in Engineering are designed to meet the needs of employers by placing the emphasis on the theoretical, practical and vocational aspects of engineering within the workplace and beyond. Engineering is becoming more high profile, and therefore more in demand as a skill set, in today’s high-tech world. This course has been designed to provide you with knowledge, skills and practical experience encountered in everyday engineering environments. Contents Overview Sequential Logic Systems Bistable or Flip-Flop Truth Table Master Slave Bistable Other Types of Bistable T-type bistable (Toggle) Credits In addition to the resource below, there are supporting documents which should be used in combination with this resource. Please see: Holdsworth B, Digital Logic Design, Newnes 2002 Crisp J, Introduction to Digital Systems, Newnes 2001 Sequential Logic

3. So far the logic circuits we have examined have been what is called COMBINATIONAL . This means that the output functions generated are directly related to the value of the inputs at that moment in time. Combinational Logic Circuit Inputs Outputs The function relating each output to the inputs will be a Boolean Expression. Sequential Logic

4. In SEQUENTIAL logic systems the outputs of a logic circuit will not only be dependent upon the state of the inputs but also upon the previous state of the outputs. Combinational Logic Circuit Inputs Outputs Delay The state of the outputs can no longer be determined by simply examining the inputs. The simplest example of this is the cross-coupled NAND gate configuration below. Sequential Logic

5. Using the logic circuit complete the truth table: 0 0 0 0 0 0 1 1 1 1 1 1 ? 1 1 1 0 0 1 ? The problem arises with the final entry into the table: If we assume F1 is a 0 then F2 becomes a 1, which keeps F1 at 0, which is logically O.K. If we assume F1 is a 1 then F2 becomes a 0, which keeps F1 at 1, which also is logically O.K. Sequential Logic A B F1 F2 A B F1 F2 0 0 0 1 1 0 1 1

6. The states of F1 and F2 with A = B = 1 will be dependent upon something other than the state of the inputs. Consider the following sequence of events: A B F1 F2 1 1 X X (X unknown) 0  1 1 0 1  1 1 0 1 0  0 1 1 1  0 1 Sequential Logic

7. It appears that the A = B = 1 state has become state which can be determined by the previous states of A and B. If A goes low then high then F1 turns on and F2 turns off. Whilst if B goes low then high F1 turns off and F2 turns on. If we now think of this simple circuit as a storage unit which can store a single binary state (0 or 1) then we can think of F1 as the output ( ) and F2 as the complementary output ( ). The A input becomes a set or turn on input (active low) and B becomes a reset or turn off input (once again active low). With both inputs at 1 the output remains at its previous state and with both inputs at 0 (set and reset simultaneously) the output is meaningless (unallowable).

8. We can now re-label the circuit which we will call a bistable or flip-flop. The truth table can be written as: 0 0 Not allowed 0 1 1 1 0 0 1 1 Storage state

9. The unit described is called an R S Bistable. (Reset Set) This unit forms the basis of storage elements within electronic memories. If this forms a design unit within a sequential system then it needs to have the ability to be synchronised with other parts of the circuit. What we mean by this is that we can determine the moment in time when output changes will occur. If one of the two inputs change then with the present set-up the output will change immediately. This will often be undesirable as we wish system units to all change their outputs at a given moment in time, determined by us. Sequential Logic

10. To allow this to happen we use a synchronising input to all units called the clock Ck . It is incorporated into the bistable in the following way: When using clocked logic elements we use a convention to specify the state of inputs prior to the clock and after the clock. Before we use and after the clock we use Sequential Logic

11. The truth table therefore looks like: Note that due to the inversion through the NAND gates on the inputs the set and reset inputs are now active high not active low. The only time now that the inputs are effective is when the clock is at logic 1: When Ck = 0 both NAND outputs are 1 and this is the storage state for the original bistable. When Ck = 1 then the NAND outputs are the inversion of the S and R values. This is called a Clocked R S Bistable 0 0 0 1 0 1 0 1 1 1 Indeterminate

12. Sometimes synchronisation has to be at a very well defined moment in time. The time when Ck is high may be too long to be sure of correct synchronisation. To ensure synchronisation is exact we must not use a level trigger but an edge trigger. See below: Ck Level triggered Edge triggered The arrows indicate the duration or the instant of the clock. Sequential Logic Positive Edge or Rising Edge Negative Edge or Falling Edge

13. This can be achieved by using what is called a Master Slave Bistable. See below: Master Slave The operation is as follows: When Ck is at 0, the Master bistable is disabled (locked) and its outputs and are fixed at their value. The Slave will be enabled (unlocked) and its outputs and will simply reflect the values on its and inputs which are the outputs of the Master. 0 1

14. As the Ck input changes to 1 the Slave becomes disabled locking the output values. The Master becomes enabled ( unlocked ) and the and inputs can now have their effect on the Master’s output. Nothing happens on the Slave output as it is locked. As the Ck input changes from 1 to 0 the Master outputs become locked and the Slave becomes unlocked. The Slave now reflects the Masters output. 1 0 Sequential Logic

15. This is therefore a falling edge triggered master slave R S bistable. The symbol for this is the same as the level triggered variety. Sequential Logic

16. Other types of bistable D-type bistable (Data) If these are connected in parallel, they can be used to produce a register see below: Sequential Logic

17. When the clock Ck input is pulsed, whatever number that is on inputs D3 to D0 will be transferred onto the outputs Q3 to Q0. This can form the basis of a register connected to a data bus. The values on the data bus (D inputs) can change and the only time they are referenced is when the clock operates. Many of these registers are found within microprocessor central processing units to hold information. The actual size (number of bits) will depend upon the size of the information being stored. In our case it is a simple 4 bit register. D3 D2 D1 D0 Q3 Q2 Q1 Q0 Ck

18. If instead of being connected in parallel they are serially connected then we form what is called a shift register. See below. Information appearing on the input will be moved one place to the right each time a clock pulse occurs e.g. if the sequence 1 then 0 then 1 then 1 is placed on the input then the following occurs as the clock changes Sequential Logic QA QD QC QB Ck Input

19. First pulse Second pulse Third pulse Fourth pulse 1 1 1 0 The Serial information (information coming in bit by bit) is now available on the Q outputs in parallel. Sequential Logic Clock pulse Input QA QB QC QD X X X X 1 X X 0 1 1 X 0 1 1 1 0 1 X X X

20. T-type bistable (Toggle) Each time a clock pulse occurs the values of and change state. This is a toggling operation. Such a bistable can be used to produce a halving of an input frequency. See below: Input Output Input Output

21. Note that the change in output occurs on the falling edge of the clock input. A row of these can be used to  2,  4,  8,  16, etc. Sequential Logic

22. An important development of the R. S. bistable is the J. K. bistable. This has the following logic circuit: Fill in the Truth Table below 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 The same Always 0 Always 1 Opposite 0 0 0 } 0 0 1 0 1 0 } 0 1 1 1 0 0 } 1 0 1 1 1 0 } 1 1 1

23. From the table we can say that the truth table for a J. K. bistable is: The symbol adopted is as follows: Note that the symbol has two extra inputs which are the Preset input and the Clear input. They have the same effect as the J and K but they are asynchronous inputs – this means that they do not require the operation of the clock input for them to operate. Also they tend to be active low inputs which mean that to make them operate we need to apply a logic ‘0’. When not in use they are connected to logic ‘1’. 0 0 0 1 1 0 1 1

24. Example using a Shift Register QA QD QC QB Ck Sequential Logic

25. Clock pulse QA QB QC QD EXNOR O/P Number 0 0 0 0 0 1 st 2 nd 3 rd 4 th 5 th 6 th 7 th 8 th 9 th 10 th 11 th 12 th 13 th 14 th 15 th

26. This resource was created by the University of Wales Newport and released as an open educational resource through the Open Engineering Resources project of the HE Academy Engineering Subject Centre. The Open Engineering Resources project was funded by HEFCE and part of the JISC/HE Academy UKOER programme. © 2009 University of Wales Newport This work is licensed under a Creative Commons Attribution 2.0 License . The JISC logo is licensed under the terms of the Creative Commons Attribution-Non-Commercial-No Derivative Works 2.0 UK: England & Wales Licence. All reproductions must comply with the terms of that licence. The HEA logo is owned by the Higher Education Academy Limited may be freely distributed and copied for educational purposes only, provided that appropriate acknowledgement is given to the Higher Education Academy as the copyright holder and original publisher. The name and logo of University of Wales Newport is a trade mark and all rights in it are reserved. The name and logo should not be reproduced without the express authorisation of the University. Sequential Logic