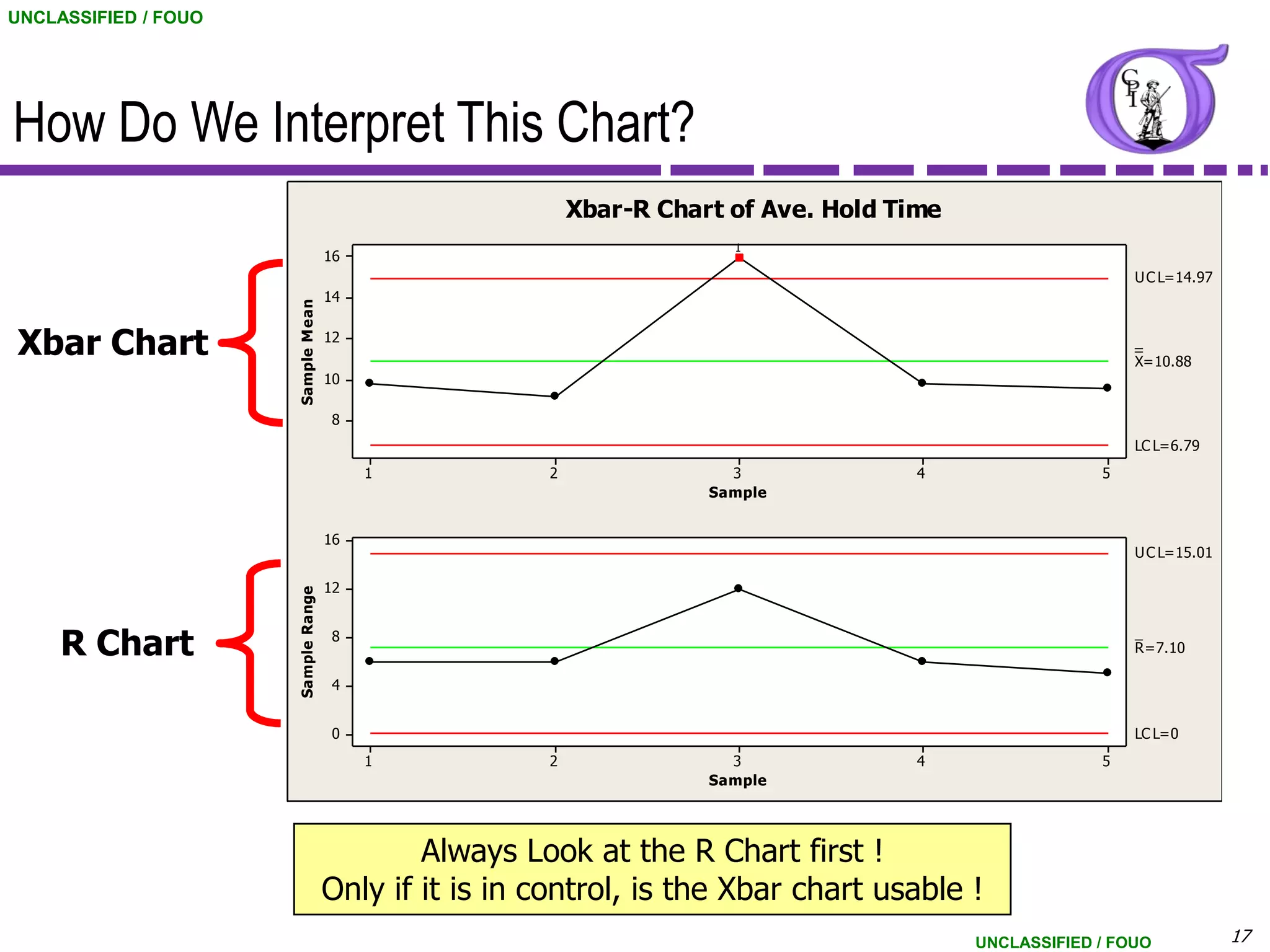
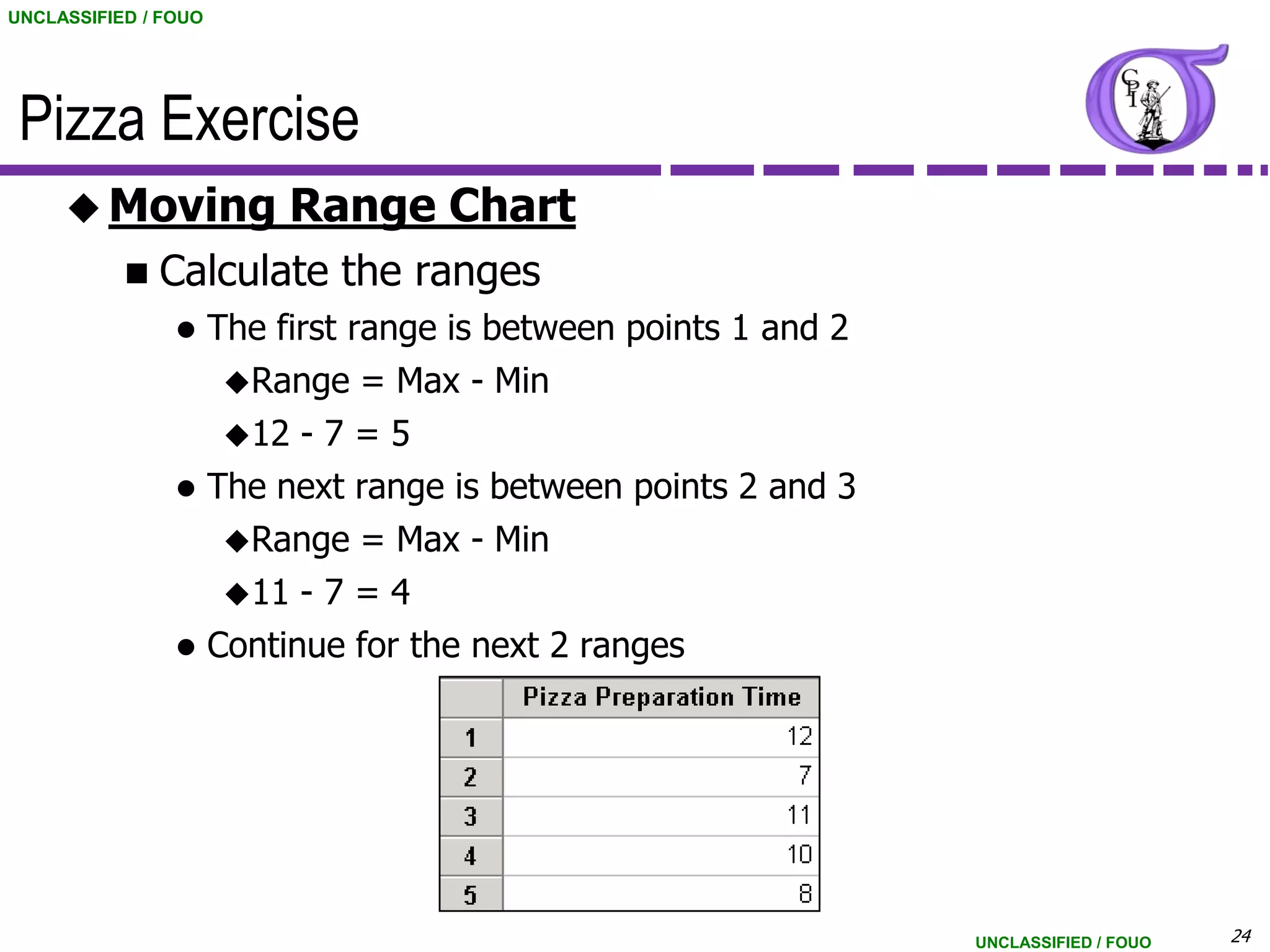
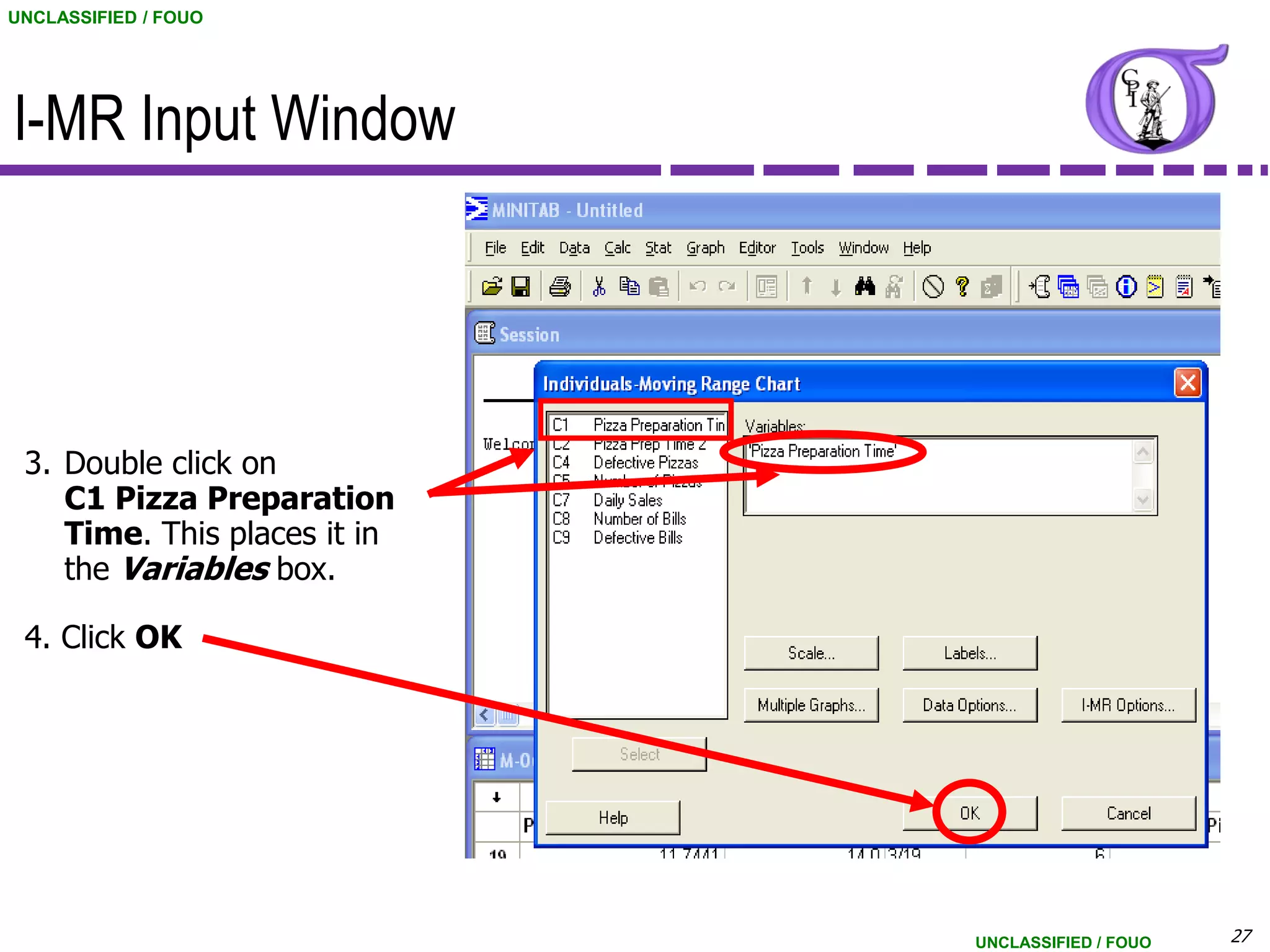
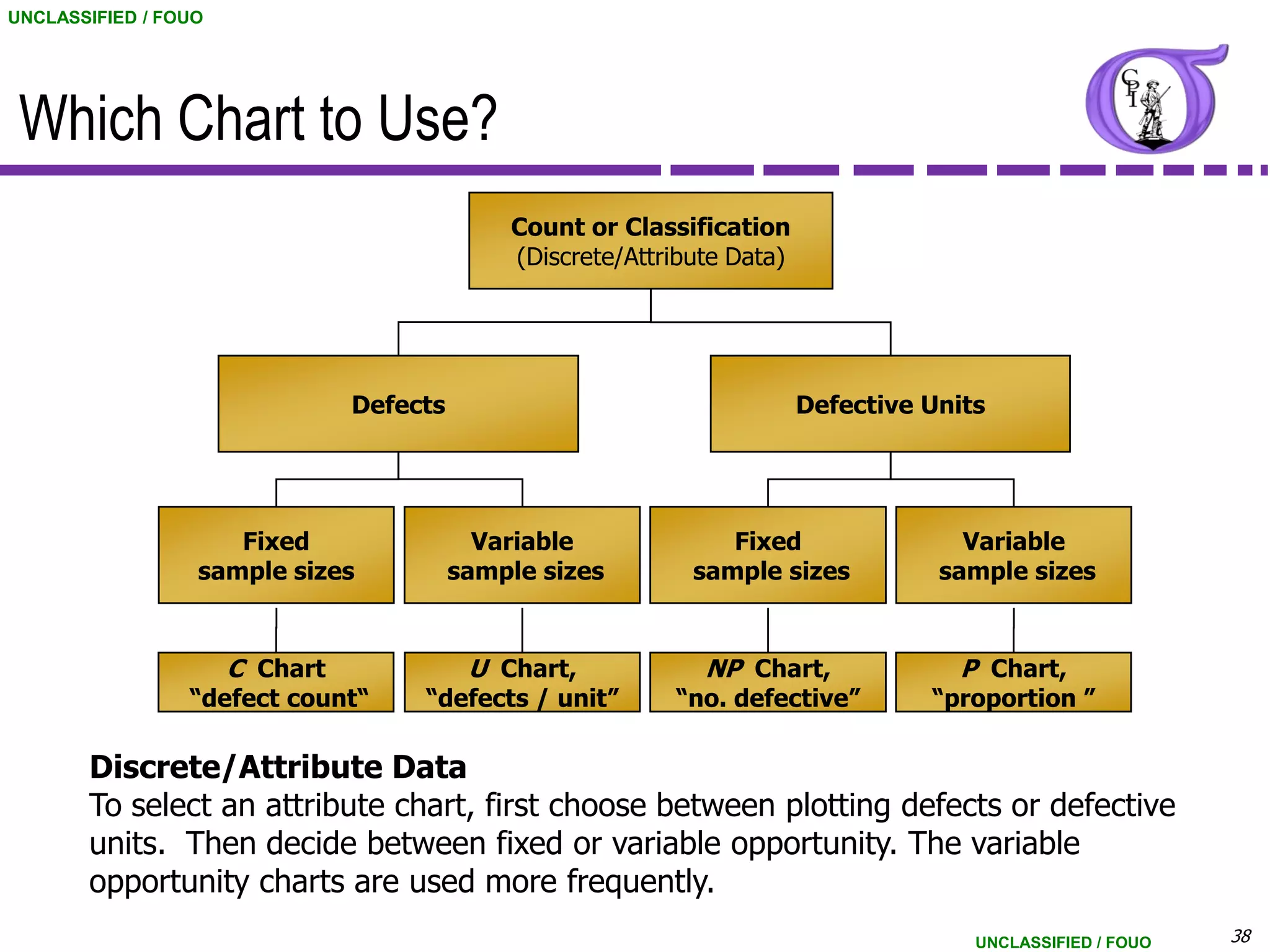
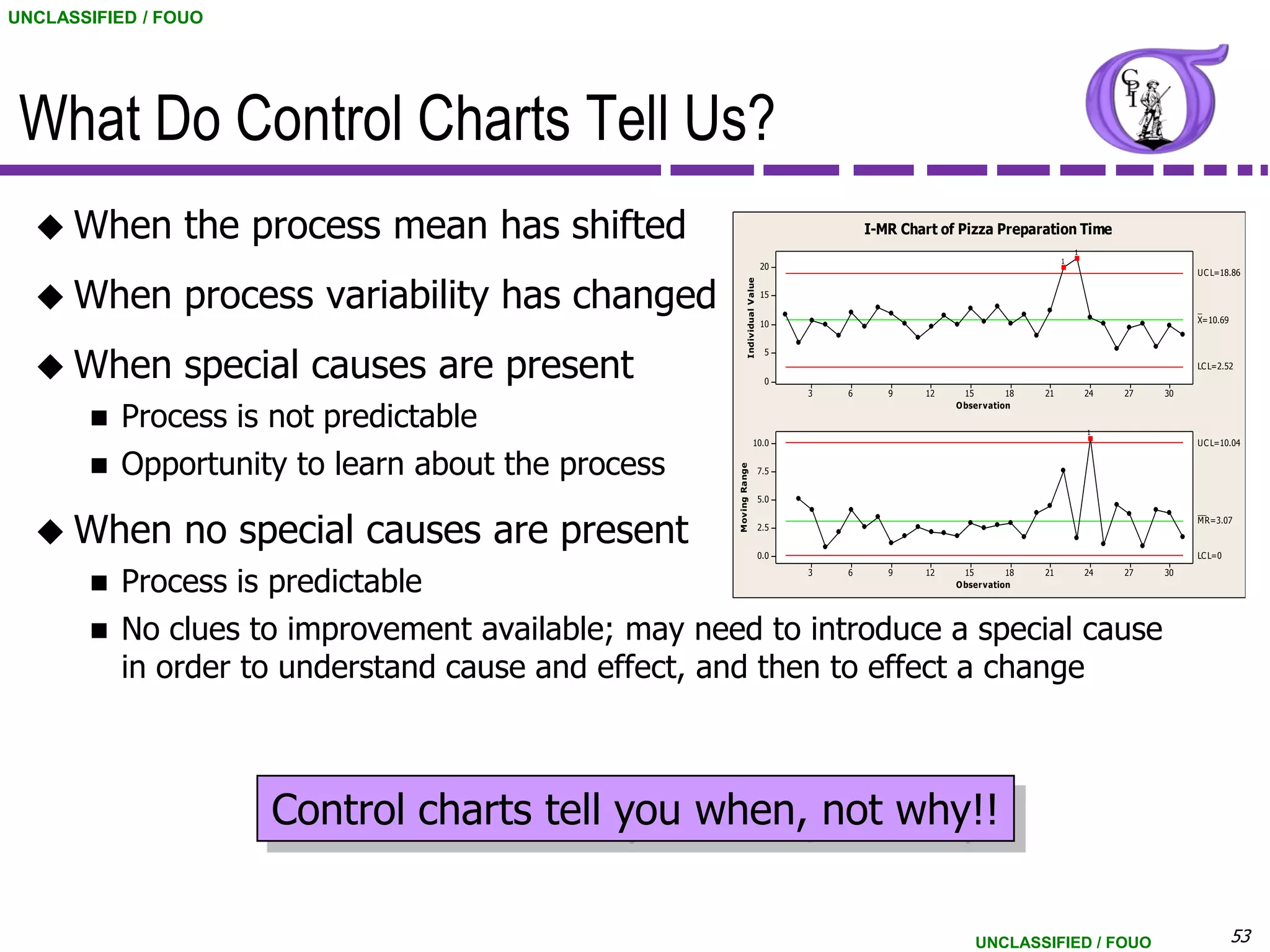
This document provides an overview of control charts for continuous data. It discusses control chart fundamentals like control limits and distinguishing between common and special cause variation. It introduces the X-bar and R chart used for variable data with subgroup sizes of 3-9. An example X-bar and R chart is presented using data on customer hold times. The document also covers the Individuals and Moving Range chart which can be used when the subgroup size is 1. Control chart assumptions and interpretation of control limits are explained.

1. UNCLASSIFIED / FOUO
National Guard
Black Belt Training
Module 26
Control Charts
UNCLASSIFIED / FOUO

2. UNCLASSIFIED / FOUO
CPI Roadmap – Measure
8-STEP PROCESS
6. See
1.Validate 2. Identify 3. Set 4. Determine 5. Develop 7. Confirm 8. Standardize
Counter-
the Performance Improvement Root Counter- Results Successful
Measures
Problem Gaps Targets Cause Measures & Process Processes
Through
Define Measure Analyze Improve Control
TOOLS
•Process Mapping
ACTIVITIES
• Map Current Process / Go & See •Process Cycle Efficiency/TOC
• Identify Key Input, Process, Output Metrics •Little’s Law
• Develop Operational Definitions •Operational Definitions
• Develop Data Collection Plan •Data Collection Plan
• Validate Measurement System •Statistical Sampling
• Collect Baseline Data •Measurement System Analysis
• Identify Performance Gaps •TPM
• Estimate Financial/Operational Benefits •Generic Pull
• Determine Process Stability/Capability •Setup Reduction
• Complete Measure Tollgate •Control Charts
•Histograms
•Constraint Identification
•Process Capability
Note: Activities and tools vary by project. Lists provided here are not necessarily all-inclusive. UNCLASSIFIED / FOUO

3. UNCLASSIFIED / FOUO
Learning Objectives
 Control chart fundamentals
 Use of control charts to identify Common Cause and
Special Cause variation
 Factors to consider in constructing control charts
 Variables control charts
 Attribute control charts
 Understand the interpretation and application of these
charts
UNCLASSIFIED / FOUO 3

4. UNCLASSIFIED / FOUO
Control Chart Terms
Control Chart = a time plot showing process
performance, mean (average), and control limits
The Voice of the Process !!!
I-MR Chart of Pizza Preparation Time
1
20
U C L=18.48
Individual Value
15
_
10 X=10.58
5
LC L=2.67
3 6 9 12 15 18 21 24 27 30
Control charts measure the “health” of the process
O bse r v ation
10.0 U C L=9.71
7.5
Moving Range
5.0
__
M R=2.97
2.5
0.0 LC L=0
3 6 9 12 15 18 21 24 27 30
O bse r v ation
UNCLASSIFIED / FOUO

5. UNCLASSIFIED / FOUO
Control Chart Terms
 Control Limits = statistically calculated boundaries
within which a process in control should operate
 These boundaries result from the process itself and are
NOT customer specifications
I-MR Chart of Pizza Preparation Time
1
20
U C L=18.48
Individual Value
15
_
10 X=10.58
5
LC L=2.67
3 6 9 12 15 18 21 24 27 30
O bse r v a tion
10.0 U C L=9.71
7.5
Moving Range
5.0
__
M R=2.97
2.5
0.0 LC L=0
3 6 9 12 15 18 21 24 27 30
O bse r v a tion
UNCLASSIFIED / FOUO 5

6. UNCLASSIFIED / FOUO
Common vs. Special Cause
 Measurements display variation
 Variation is either:
 Common Cause Variation
 This is the consistent, stable, random variability within the process
 We will have to make a fundamental improvement to reduce common
cause variation
 Is usually harder to reduce
 Special Cause Variation
 This is due to a specific cause that we can isolate
 Special cause variation can be detected by spotting outliers or
patterns in the data
 Usually easier to eliminate
UNCLASSIFIED / FOUO 6

7. UNCLASSIFIED / FOUO
Process Control
 When a process is “in control”
 This implies a stable, predictable amount of variation (common
cause variation)
 This does not mean a "good" or desirable amount of variation
 When a process is “out-of-control”
 This implies an unstable, unpredictable amount of variation
 It is subject to both common AND special causes of variation
 A process can be in statistical control and not capable of consistently
producing good output within specification limits
UNCLASSIFIED / FOUO 7

8. UNCLASSIFIED / FOUO
Types of Control Charts
 The Control Chart family can be broken into two groups
based on the type of data we are charting:
 Continuous/Variable
 Attribute/Discrete
 Since we “prefer” Continuous data we will study this group
of Control Charts first
UNCLASSIFIED / FOUO 8

9. UNCLASSIFIED / FOUO
Continuous Data Control Charts
 The theory of all Control Charts can be learned by studying
the Xbar (Average) and R (Range) chart for continuous
data
 We will then explore the I-MR (Individuals - Moving Range)
Chart
 Xbar-R Charts allow us to study:
 Variation “within each subgroup” (precision) on the R chart
 Variation “between each subgroup” (accuracy) on the Xbar chart
 Note: Look at the R chart first, if it is in control, then look at the
Xbar chart
 Examples of continuous data: width, diameter,
temperature, weight, cycle times, etc.
UNCLASSIFIED / FOUO 9

10. UNCLASSIFIED / FOUO
Control Chart Assumptions
 Normally Distributed Data
 Control limits approximate +/- 3 sigma from the mean
 These control limits are based upon a normal distribution
 If the distribution of the data is non-normal, you must use one of the
x-bar charts, because the x-bars are likely to be normally distributed
due to the effects of the Central Limit Theorem
 Rule of thumb for x-bar charts is subgroups of at least 4. Rarely is
the underlying distribution so far from normal to require larger
subgroups to achieve normality in the x-bars.
 Independent Data Points
 “Independence” means the value of any given data point is not
influenced by the value of any other data point (it is random)
 Violation of this assumption means the probability of any given data
value occurring is not determined by its distance from the mean, but
by its place in the sequence in a data series or pattern
UNCLASSIFIED / FOUO 10

11. UNCLASSIFIED / FOUO
Continuous Data Control Charts
Measurement
(Continuous/Variable Data)
Subgroup Size of 1 Subgroup Size < 3-9 Subgroup Size > 9
I-MR Xbar-R Xbar-S
UNCLASSIFIED / FOUO 11

12. UNCLASSIFIED / FOUO
Continuous Data Control Charts
 Utilize probabilities and knowledge of the normal distribution
 I-MR chart is used:
 When you are learning about a process with few data points
 When sampling is very expensive
 When the sampling is by destructive testing and
 When you are building data to begin another chart type
 Xbar-R Chart is used with a sampling plan to monitor repetitive
processes. The sub-group sizes are from 3 to 9 items. Frequently
practitioners will choose subgroups of 5. All of the theory of Control
Charts can be applied with these charts
 Xbar-S Chart is used with larger sample groups of 10 or more items.
Statisticians sometimes state that the standard deviation is only robust
when the subgroup size is greater than 9 (These charts are similar to
the Xbar-R Chart)
UNCLASSIFIED / FOUO 12

13. UNCLASSIFIED / FOUO
Introduction to Xbar-R
 Xbar-R Charts are a way of displaying variable data
 Examples of variable data: width, diameter, temperature, weight,
time, etc.
R Chart: a look at “Precision”
 Displays changes in the „within‟ subgroup dispersion of the
process. Often called “Short-Term Variation.”
 Asks "Is the variation in the measurements „within‟ subgroups
consistent?”
 Must be “in control” before we can build or use the Xbar chart
 Xbar Chart: a look at “Accuracy”
 Shows changes in the average value of the process and is a
visualization of the “Longer-Term Variation”
 Asks "Is the variation „between‟ the averages of the subgroups
more than that predicted by the variation within the subgroups?“
UNCLASSIFIED / FOUO 13

14. UNCLASSIFIED / FOUO
Mechanics of an Xbar-R Chart
 Control charts track processes by plotting data over
time in the form:
Range Chart X Chart
Upper Control Limit Averages
Upper Control Limit
Chart = X Double Bar + A2 R Bar Upper Control Limit
Range Chart = D4Rbar Upper Control Limit
Center Line Averages Chart =
Average of the Subgroup Averages Center Line (X)
Center Line Range Chart =
Average of the Subgroup Ranges Center Line (R) Lower Control Limit Averages
Chart = X Double Bar - A2 R Bar Lower Control Limit
Lower Control Limit
Range Chart = D3Rbar
UNCLASSIFIED / FOUO 14

15. UNCLASSIFIED / FOUO
Example: Xbar-R Chart
Stat > Control Charts > Variables Charts for Subgroups > Xbar-R
Open the worksheet data file called ORDER TAKING.MTW
In this file, orders are taken by order entry clerks. The data is the average hold
time a customer waits before speaking with a person to take their order.
The delays are a problem, as many customers give up and we have a dropped call
and lost order
UNCLASSIFIED / FOUO 15

16. UNCLASSIFIED / FOUO
Example: Xbar-R Chart
Double click on
C-1 Ave Hold Time
This places it in the 5
Variables box
Type in 5 for your
Subgroup size
Our response is Ave. Hold Time and we choose
5 cells to represent our Subgroup size
UNCLASSIFIED / FOUO 16

17. UNCLASSIFIED / FOUO
How Do We Interpret This Chart?
Xbar-R Chart of Ave. Hold Time
1
16
U C L=14.97
14
Sample M ean
Xbar Chart 12 _
_
X=10.88
10
8
LC L=6.79
1 2 3 4 5
Sample
16
U C L=15.01
12
Sample Range
R Chart 8 _
R=7.10
4
0 LC L=0
1 2 3 4 5
Sample
Always Look at the R Chart first !
Only if it is in control, is the Xbar chart usable !
UNCLASSIFIED / FOUO 17

18. UNCLASSIFIED / FOUO
Control Chart Data Requirements
 Data requirements for control chart applications:
 Must be in time series order
 Minimum of 25 consecutive (no time gaps) subgroups
or
 Minimum of 100 consecutive observations
UNCLASSIFIED / FOUO 18

19. UNCLASSIFIED / FOUO
I-MR Chart
 The Individuals and Moving Range chart is also for
continuous data
 It can be used for many transactional applications:
 Revenue or cost tracking
 Customer satisfaction
 Call times
 System response times
 Wait times
 Most common continuous measures – time and money!
UNCLASSIFIED / FOUO 19

20. UNCLASSIFIED / FOUO
Individuals and Moving Range (I-MR) Chart
I-MR Chart of Pizza Preparation Time
1
20
U C L=18.48
Individual Value
15
_
10 X=10.58
5
LC L=2.67
3 6 9 12 15 18 21 24 27 30
O bse r v ation
10.0 U C L=9.71
7.5
Moving Range
5.0
__
M R=2.97
2.5
0.0 LC L=0
3 6 9 12 15 18 21 24 27 30
O bse r v ation
 The top chart is a plot of individual pizza preparation times
 The bottom chart is the Moving Range, in this case, the Range of two
adjacent pizza preparation times
UNCLASSIFIED / FOUO 20

21. UNCLASSIFIED / FOUO
Control Limit Calculation
I Chart of Pizza Preparation Time
1
20
UCL=18.48
UCL
15
Individual Value
_ X
X=10.58
10
5
LCL
LCL=2.67
3 6 9 12 15 18 21 24 27 30
Observat ion
 The UCL (Upper Control Limit) and the LCL (Lower Control Limit) are
calculated by Minitab using the sample/process data
 The control limits approximate +/- 3 standard deviations (99+% of the data)
 Here, 99+% of the pizzas are prepared between 2.6 and 18.7 minutes
 Be careful not to confuse control limits and specification limits! If a data
point appears outside of the control limits, there is less than a 1% chance
that this was part of the normal process. Since it is very unlikely that this
value occurred by chance, it is called “Special Cause” variation.
UNCLASSIFIED / FOUO 21

22. UNCLASSIFIED / FOUO
Control Limit Interpretation
I Chart of Pizza Prep Time 2
1
20.0
17.5 1
15.0 UCL=15.29
Individual Value
12.5
_
10.0 X=9.87
7.5 3 3
3 3 3
3 3 3
5.0
3 LCL=4.45
3 6 9 12 15 18 21 24 27
Observation
 Another type of Special Cause variation occurs when there is a predictable
pattern in the data
 The predictable pattern of the data means the data is not random and that
there is an underlying reason for this pattern – a Special Cause
 The Western Electric rules are helpful in identifying patterns in the data
(these are in the appendix)
UNCLASSIFIED / FOUO 22

23. UNCLASSIFIED / FOUO
Exercise: Begin Building an I-MR Chart
 Let‟s begin building an I-MR chart for a Pizza Preparation process.
Begin by using the 5 Pizza Preparation Time measurements below
to start the calculations for a Control Chart on a flip-chart.
 Individuals Chart
 Plot each individual time measurement
 Calculate the Centerline
 The centerline on an Individuals chart is the overall average
 Verify that the average is 9.6
 The control limits will be calculated by a formula in Minitab. They
approximate +/- 3 standard deviations of the pizza prep times
UNCLASSIFIED / FOUO 23

24. UNCLASSIFIED / FOUO
Pizza Exercise
 Moving Range Chart
 Calculate the ranges
 The first range is between points 1 and 2
Range = Max - Min
12 - 7 = 5
 The next range is between points 2 and 3
Range = Max - Min
11 - 7 = 4
 Continue for the next 2 ranges
UNCLASSIFIED / FOUO 24

25. UNCLASSIFIED / FOUO
Pizza Exercise (Cont.)
 Moving Range Chart
 Calculate the Centerline
 The centerline is the average of the moving ranges, called R
 For these 5 points (4 range calculations), verify that R = 3
 The Control Limits will be calculated in Minitab. In this case
they approximate +/- 3 standard deviations of the range
values.
 We expect the Control Limits to be tighter for the Moving
Range chart than for the Individuals chart
UNCLASSIFIED / FOUO 25

26. UNCLASSIFIED / FOUO
Build I-MR Chart in Minitab
 Let‟s continue with
our exercise:
1. Open the exercise
Exercise9.mtw
2. Choose:
Stat>
Control Charts>
Variables Charts for
Individuals>
I-MR
UNCLASSIFIED / FOUO 26

27. UNCLASSIFIED / FOUO
I-MR Input Window
3. Double click on
C1 Pizza Preparation
Time. This places it in
the Variables box.
4. Click OK
UNCLASSIFIED / FOUO 27

28. UNCLASSIFIED / FOUO
Individual and Moving Range (I-MR) Chart
I-MR Chart of Pizza Preparation Time
1
20
U C L=18.48
Individual Value
15
_
10 X=10.58
5
LC L=2.67
3 6 9 12 15 18 21 24 27 30
O bser vation
10.0 U C L=9.71
7.5
M oving Range
5.0
__
M R=2.97
2.5
0.0 LC L=0
3 6 9 12 15 18 21 24 27 30
O bser vation
Is our Pizza Prep process in statistical control?
Is the process likely to be acceptable to our customers?
UNCLASSIFIED / FOUO 28

29. UNCLASSIFIED / FOUO
Western Electric Rules
 Remember the tests that we used in Run Charts? These are used in
Control Charts as well.
 The additional tests are called the “Western Electric Rules”
 They can be found under Stat>Control Charts>Variables Charts for
Individuals>I-MR>I-MR Options>Tests
UNCLASSIFIED / FOUO 29

30. UNCLASSIFIED / FOUO
Control Chart Tests
Upper Control Limit Point outside of the limit:
Control limits are calculated to measure the
Center Line
natural variability of a process. Any point on, or
outside, the limit is considered
Lower Control Limit abnormal and requires investigation.
Run:
Upper Control Limit A “run” is a series of points occurring
Center Line continually on one side of the center line. A
“run” of seven points is considered abnormal.
Lower Control Limit Also considered abnormal: 10 out of 11,12 of 14,
or 16 of 20 points on one
side of the center line.
Upper Control Limit
Trending:
Center Line Seven points in a continuous upward or
downward direction.
Lower Control Limit
UNCLASSIFIED / FOUO

31. UNCLASSIFIED / FOUO
Control Chart Tests
Upper Control Limit Approaching the center line (hugging):
When most points lie within the center line and
1.5s it is not a controlled state and usually means
CL the mixing of data from different populations. This
Lower Control Limit makes the control limits too wide and
stratification of data is usually necessary.
Upper Control Limit
Cycling (periodicity):
CL Any repeated up and down trend is abnormal
and requires investigation.
Lower Control Limit
UCL
Approaching control limits:
CL 2 of 3 points lying outside the
2s line is considered abnormal.
LCL
UNCLASSIFIED / FOUO

32. UNCLASSIFIED / FOUO
Special Causes Are Clues to the Process
 A control chart is a guide to improving your process
 Take advantage of every clue
 Identify and investigate all special causes – they
teach us how things affect the process
 Some special causes are good!
 For example, in our pizza delivery case, a delivery time
out of control on the low side would be good. We
could investigate this case to try to discover a new best
practice.
UNCLASSIFIED / FOUO 32

33. UNCLASSIFIED / FOUO
Process for Identifying Special Causes
 Check all the W.E. rules each time you plot a point
 Look across the entire chart
 Circle all special causes
 Investigate immediately – this is especially important.
Do not lose the opportunity to learn as much as possible
about the conditions that caused this special cause
variability.
 Take notes on the investigation
 You must investigate and eliminate the special cause!
UNCLASSIFIED / FOUO 33

34. UNCLASSIFIED / FOUO
Next Steps
 Identify assignable causes
 Establish that the data are normally distributed
without the special cause data points
 Circle the special causes
 Eliminate special causes from the control limit
calculation
 Recalculate control limits
UNCLASSIFIED / FOUO 34

35. UNCLASSIFIED / FOUO
New Control Limits
I-MR Chart of Pizza Preparation Time
1
1
20
U C L=18.86
If you can investigate
Indiv idual V alue
15
and determine what 10
_
X=10.69
caused these
5
„Out of Control‟ LC L=2.52
points, you can then 0
3 6 9 12 15 18 21 24 27 30
delete them and
Observation
recalculate your 10.0
1
U C L=10.04
control chart limits
M ov ing Range
7.5
5.0
__
MR=3.07
2.5
0.0 LC L=0
3 6 9 12 15 18 21 24 27 30
Observation
UNCLASSIFIED / FOUO 35

36. UNCLASSIFIED / FOUO
Attribute Control
Charts
UNCLASSIFIED / FOUO

37. UNCLASSIFIED / FOUO
Attribute Data Charts
 Two categories of attribute data:
 Count data (outcomes: 0, 1, 2, 3, 4, 5, etc.)
 Good/bad product data (only 2 possible outcomes)
 Four common attribute charts:
 C and U charts are used for count data of
 Errors in the process, either a step in the process or the
overall process, or
 Defects in the process‟ or steps‟ deliverables
 NP and P charts are used for good/bad process,
service, or product data (items or process steps that
are defective or flawed)
UNCLASSIFIED / FOUO 37

38. UNCLASSIFIED / FOUO
Which Chart to Use?
Count or Classification
(Discrete/Attribute Data)
Defects Defective Units
Fixed Variable Fixed Variable
sample sizes sample sizes sample sizes sample sizes
C Chart U Chart, NP Chart, P Chart,
“defect count“ “defects / unit” “no. defective” “proportion ”
Discrete/Attribute Data
To select an attribute chart, first choose between plotting defects or defective
units. Then decide between fixed or variable opportunity. The variable
opportunity charts are used more frequently.
UNCLASSIFIED / FOUO 38

39. UNCLASSIFIED / FOUO
Deeper into Attribute Charts
 Many transactional processes and manufacturing processes only
record data as to the service or the products being either bad
or good, defective or not defective
 There are two sub-families in the Attribute control charts:
 If we count defects (usually with any item having more
than one opportunity for a defect) we use the C or
Ucharts
 If the sample size is always the same, use a C-chart. If the
sample size varies, use a U-chart.
 If we count defective units instead of defects, we use
the NP or P charts
 If the sample size is always the same, use a NP-chart. If the
sample size varies, use a P-chart.
UNCLASSIFIED / FOUO 39

40. UNCLASSIFIED / FOUO
Charts for Attribute Data
 Most of the Attribute Control Charts are identical in
interpretation and very similar to create in Minitab
 The equations used are slightly different, but still
based on the theory we learned with the Xbar Chart
 One of the most commonly used attribute charts is
the P-Chart which plots Proportion Defective
 If you calculated Proportion Defective as your
baseline capability metric – this chart is for you!
UNCLASSIFIED / FOUO 40

41. UNCLASSIFIED / FOUO
P-Chart
 P-Charts should be used whenever we are monitoring
proportion defective (percentage defective is just another
proportion)
 Some uses of the P-Chart in transactional applications would
be:
 Billing errors (proportion of total bills that had errors)
 Defective loan applications
 Proportion of invoices with errors
 Proportion of missing reservations
 Defective room service orders
 Missing items
 Proportion of customers who were dissatisfied with service
UNCLASSIFIED / FOUO 41

42. UNCLASSIFIED / FOUO
P-Chart Pizza Exercise
 Anthony's Pizza wishes to monitor defective pizzas
 Each day for a month the cook keeps a count of the
number of defective pizzas for that day and also the
total number of pizzas that day
 Let‟s use the first 5 days data below to start the P-
Chart on a flipchart
UNCLASSIFIED / FOUO 42

43. UNCLASSIFIED / FOUO
P-Chart Pizza Exercise (Cont.)
 Calculate the proportion defective
 Recall the formula for proportion defective:
Number of Defective Units
Proportion Defective 
Total Units
 In this example:
Number of Defective Pizzas
Proportion Defective 
Total Pizzas
 For the first day:
9
Proportion Defective   0.021
420
Note: Percentage Defective, in this case,
would be 2.1% defective
 Calculate the proportion defective for days 2-5
UNCLASSIFIED / FOUO 43

44. UNCLASSIFIED / FOUO
P-Chart Pizza Exercise (Cont.)
 Next, calculate the center line
 The center line is the proportion of Total Defectives
(for all samples) to Total Units (for all samples)
 Verify that this is 0.019
 The Control Limits are calculated in Minitab
 The equations are slightly different, but the Control Limits
are still calculated from the actual values, predicting the
range of 99% of the data
UNCLASSIFIED / FOUO 44

45. UNCLASSIFIED / FOUO
Minitab - Attributes Control Charts
1. Open worksheet: Exercise9.mtw
2. Choose Stat>Control Charts>Attributes Charts>P
UNCLASSIFIED / FOUO 45

46. UNCLASSIFIED / FOUO
P-Chart Input Window
3. Double click on
C-4 Defective Pizzas.
This places it in the
Variables box.
4. Place cursor in the
Subgroups sizes box
and then double click on
C-5 Number of Pizzas
to move it there
5. Click OK
Note: Minitab calculates the proportion defective for us. We enter the
defective units in the Variable box. Then we enter the total units over
that time period in the Subgroup sizes box.
UNCLASSIFIED / FOUO 46

47. UNCLASSIFIED / FOUO
P-Chart
P Chart of Defective Pizzas
0.05 1
Note: Minitab recalculates
0.04 the control limits every
UCL=0.03689 time the subgroup size
0.03 changes.
Proportion
To get a straight line, you
_
0.02 P=0.01932 can enter a constant value
under “Subgroup size.”
0.01
In this example, the best
LCL=0.00174 constant would be the
0.00
average of the “Number of
3 6 9 12 15 18 21 24 27 30
Sample
Pizzas.”
Tests performed with unequal sample sizes
What are your thoughts around our defective pizzas?
UNCLASSIFIED / FOUO 47

48. UNCLASSIFIED / FOUO
Exercise: Create a Control Chart
 Now Anthony's Pizza wants to investigate sales history and
billing errors for the same month
 In teams, continue with Exercise9.mtw. Use an I-
MR Chart to monitor sales for the month.
 Use a P-Chart to observe the proportion of defective
bills
 Prepare to teach back to the class on your findings
UNCLASSIFIED / FOUO 48

49. UNCLASSIFIED / FOUO
Quick Review - Control Chart Reminders
 There are several types of control charts:
 Determine type of data: continuous or attribute
 Be clear on the purpose and value you wish to gain
from the chart
 Control limits are derived from process data
UNCLASSIFIED / FOUO 49

50. UNCLASSIFIED / FOUO
Control Chart Uses and Benefits
 Demonstrate stability and predictability of a process
over time
 Range of variation within the “control limits”
 Distinguish between common vs. special cause
variation
 Provides more information than Run Charts
 Can be used to demonstrate changes in performance
 Provide a common language for process performance
 Offer early warning of problems
BUT…..
UNCLASSIFIED / FOUO 50

51. UNCLASSIFIED / FOUO
Control Chart Challenges
 Must use correct type of chart for the data
 Must meet normality and independence assumptions
 Non-normal, continuous data must use x-bar chart to meet
normality requirement
 Control limits vs. customer requirements
 Remember that the control limits are providing the Voice of the
Process
 We need to look at specification limits to see the Voice of the
Customer
 A process “in control” may be ineffective, inefficient, or both!
 Control charts require effective, ongoing data collection. To be
effective for determining root causes of special cause variation,
they must be reacted to immediately!
UNCLASSIFIED / FOUO 51

52. UNCLASSIFIED / FOUO
Steps in Control Charting
 Select process characteristic to control, the key x or Y
 Collect data and calculate appropriate statistics
 Assess data distribution normality
 Construct preliminary control charts
 Establish control (find and eliminate special causes)
 Construct final control charts
 Establish stability (find and reduce common causes)
 Use for ongoing control purposes
UNCLASSIFIED / FOUO 52

53. UNCLASSIFIED / FOUO
What Do Control Charts Tell Us?
 When the process mean has shifted I-MR Chart of Pizza Preparation Time
1
1
20
U C L=18.86
 When process variability has changed
Individual V alue
15
_
10 X=10.69
 When special causes are present
5
LC L=2.52
0
3 6 9 12 15 18 21 24 27 30
Process is not predictable
O bser vation
 1
10.0 U C L=10.04
 Opportunity to learn about the process
M oving Range
7.5
5.0
 When no special causes are present
__
M R=3.07
2.5
0.0 LC L=0
Process is predictable
3 6 9 12 15 18 21 24 27 30
 O bser vation
 No clues to improvement available; may need to introduce a special cause
in order to understand cause and effect, and then to effect a change
Control charts tell you when, not why!!
UNCLASSIFIED / FOUO 53

54. UNCLASSIFIED / FOUO
Process Control Chart Template
I-MR Chart of Delivery Time
 The current baseline
40
delivery time is stable UC L=37.70
over time with both
Indiv idual V alue
35
the Moving Range 30 _
X=29.13
(3.22 days) and 25
Individual Average
LC L=20.56
(29.13 days) 20
1 28 55 82 109 136 163 190 217 244
experiencing common Observation
cause variation 10.0
UC L=10.53
 255 data points
M ov ing Range
7.5
collected with zero 5.0
subgroups, thus the
__
MR=3.22
2.5
I&MR control chart
0.0 LC L=0
selected 1 28 55 82 109 136 163 190 217 244
Observation
- Example - Required As Applicable
UNCLASSIFIED / FOUO

55. UNCLASSIFIED / FOUO
Exercise: Prepare a Control Chart
Objective
Create control charts for the GGA's Budget Department
Instructions
 Identify Primary Y metric
 Determine best control charts to use
 Run proper control chart for that data
Time = 15 Minutes
UNCLASSIFIED / FOUO 55

56. UNCLASSIFIED / FOUO
Takeaways
 Control limits are calculated from a time series of the characteristic we are
measuring
 Different formulas are available, depending on the type of data
 Control limits should not be recalculated each time data are collected
 The control limits are a function of the sampling and subgrouping plan
 Variation due to "assignable cause" is often the easiest variation to
reduce/eliminate
 Control limits are not related to standards! Nor are they specifications!
Control limits are a measure of what the process is doing/has done. It is the
present/past tense, not the future (what we want the process to do or what it
has the potential to do)
UNCLASSIFIED / FOUO 56

57. UNCLASSIFIED / FOUO
What other comments or questions
do you have?
UNCLASSIFIED / FOUO

58. UNCLASSIFIED / FOUO
References
 Wheeler, Donald J. & Chambers, David S.,
Understanding Statistical Process Control, Second
Edition, SPC Press, Knoxville Tennessee, 1992
 Pruit, James M. & Snyder, Helmut, Essentials of SPC
in the Process Industries, Instrument Society of
America, 1996
UNCLASSIFIED / FOUO 58

59. UNCLASSIFIED / FOUO
APPENDIX
UNCLASSIFIED / FOUO

60. UNCLASSIFIED / FOUO
Western Electric Rules
1. One point beyond Zone A
 Detects a shift in the mean, an increase in the
standard deviation, or a single aberration in the
process. For interpreting Test 1, the R chart can be
used to rule out increases in variation.
2. Nine points in a row in Zone C or beyond
 Detects a shift in the process mean
3. Six points in a row steadily increasing or
decreasing
 Detects a trend or drift in the process mean. Small
trends will be signaled by this test before Test 1.
UNCLASSIFIED / FOUO 60

61. UNCLASSIFIED / FOUO
Western Electric Rules (Cont.)
4. Fourteen points in a row alternating up and down
 Detects systematic effects, such as two alternately used
machines, vendors, or operators
5. Two out of three points in a row in Zone A or
beyond
 Detects a shift in the process average or increase in the
standard deviation. Any two out of three points provide a
positive test.
6. Four out of five points in Zone B or beyond
 Detects a shift in the process mean. Any four out of five
points provide a positive test.
UNCLASSIFIED / FOUO 61

62. UNCLASSIFIED / FOUO
Western Electric Rules (Cont.)
7. Fifteen points in a row in Zone C, above and
below the center line
 Detects stratification of subgroups when the
observations in a single subgroup come from various
sources with different means
8. Eight points in a row on both sides of the
center line with none in Zone C
 Detects stratification of subgroups when the
observations in one subgroup come from a single
source, but subgroups come from different sources
with different means
UNCLASSIFIED / FOUO 62