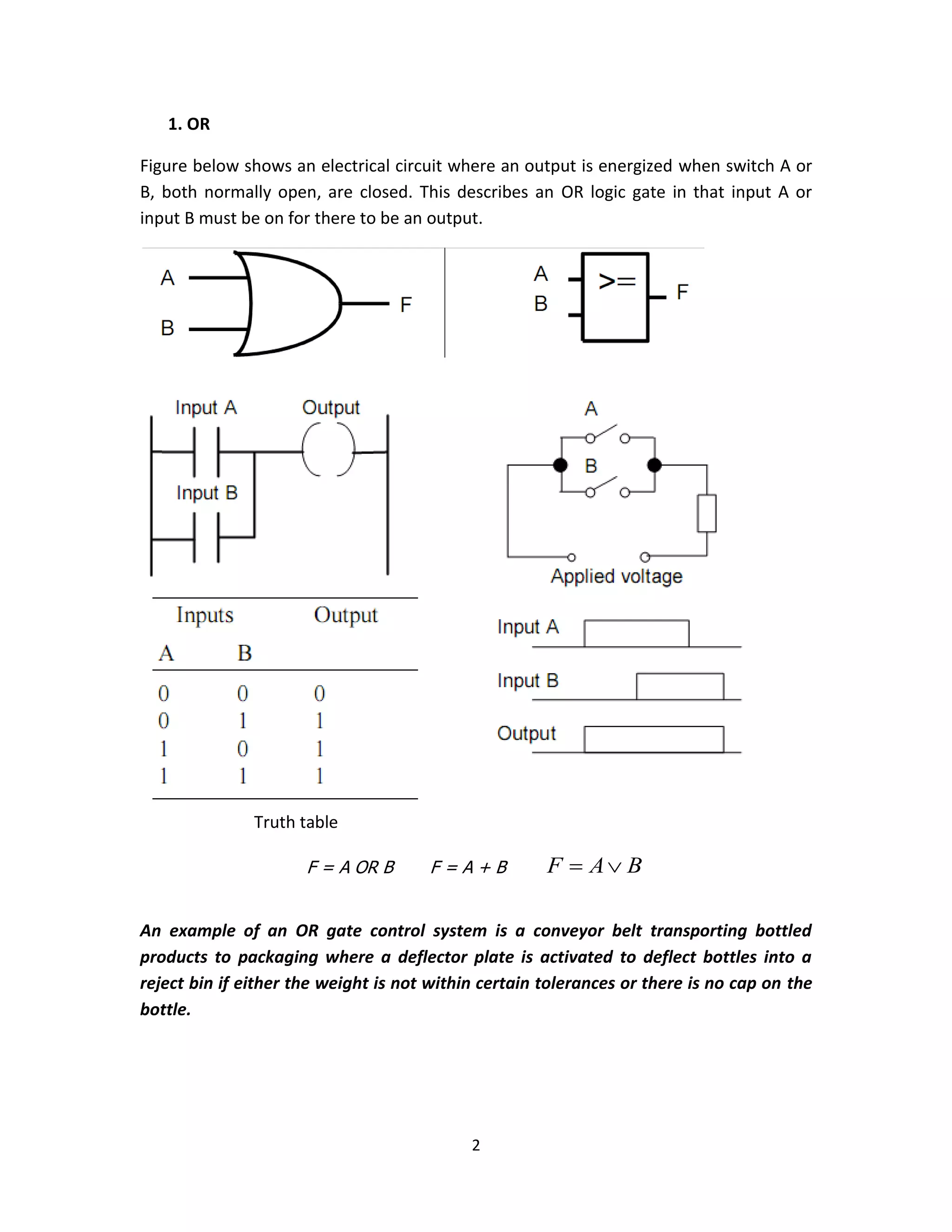
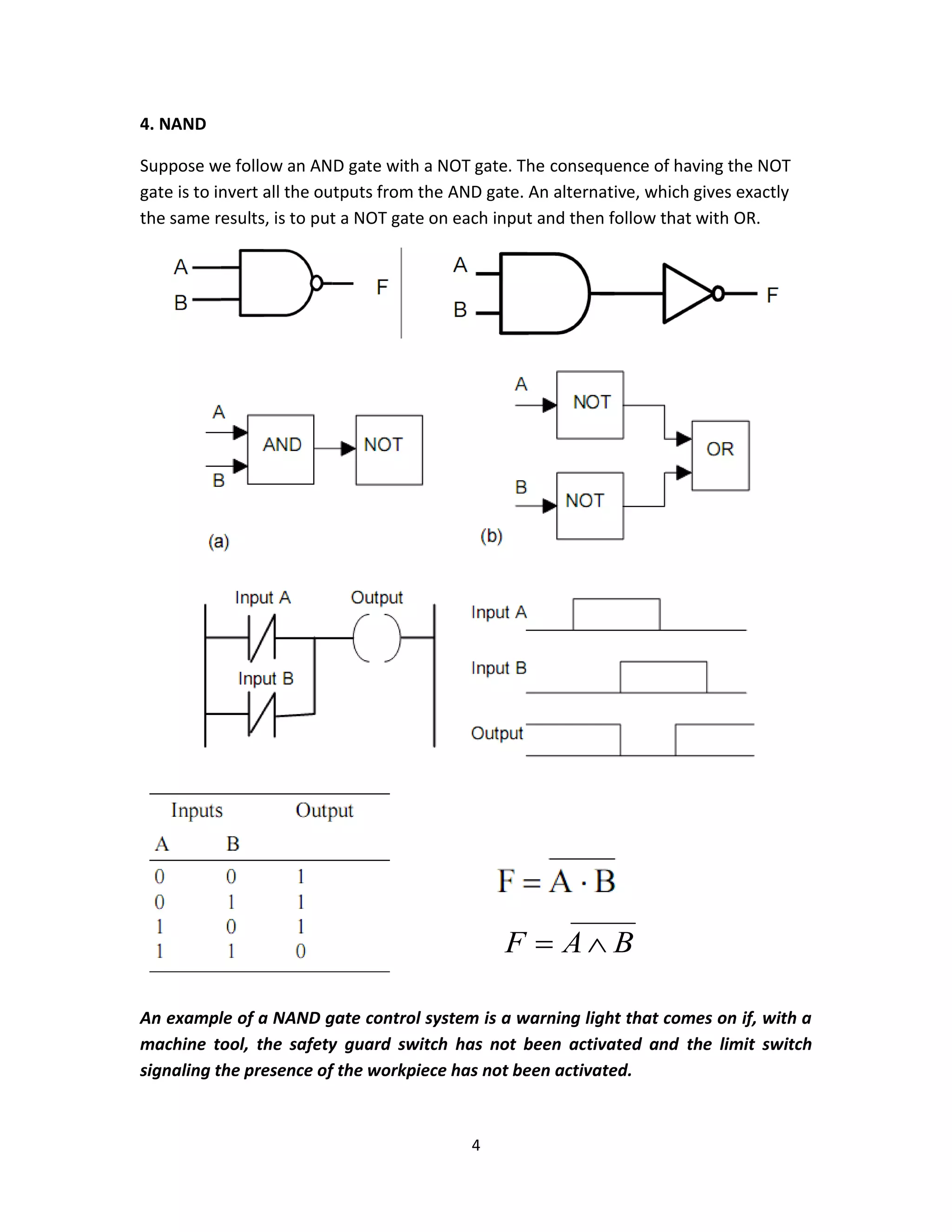
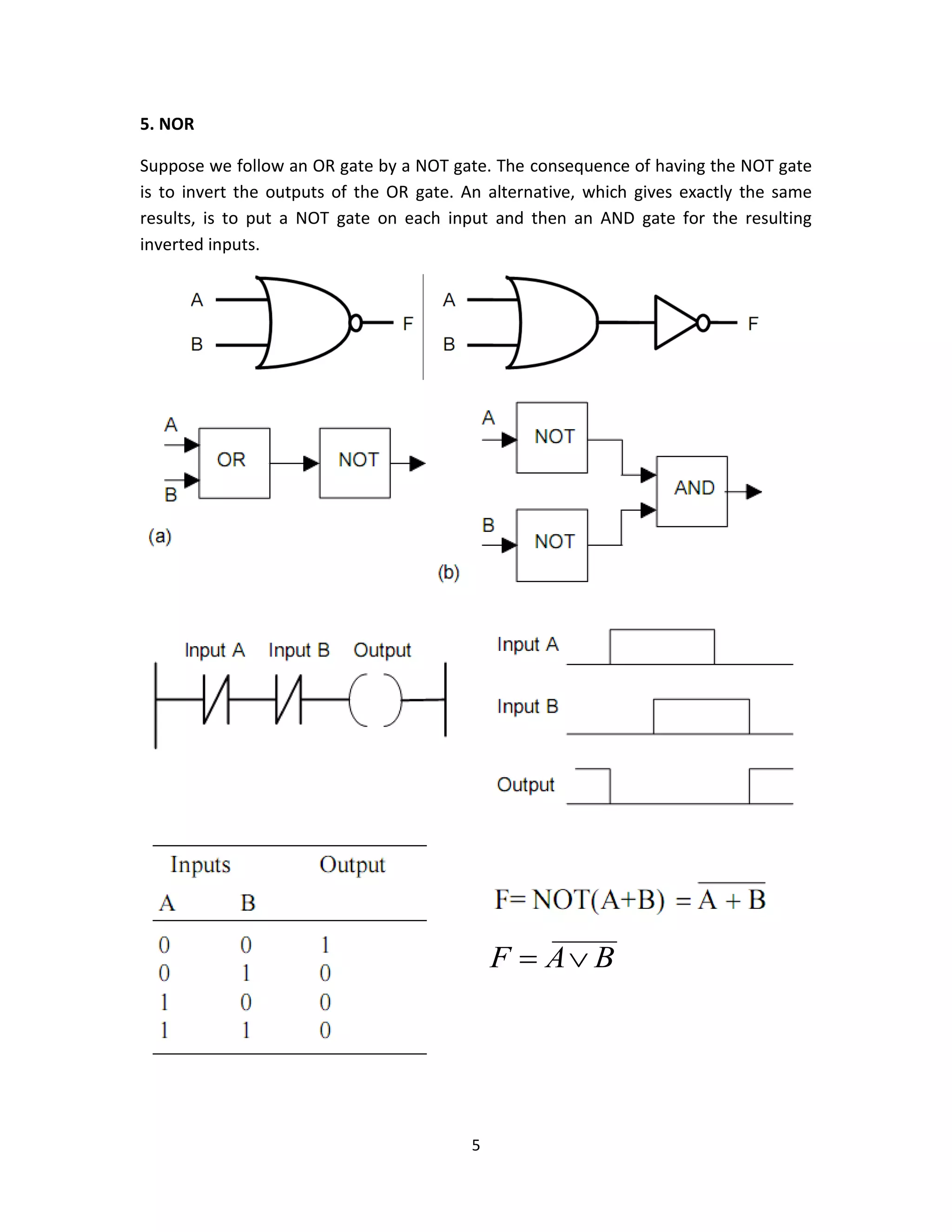
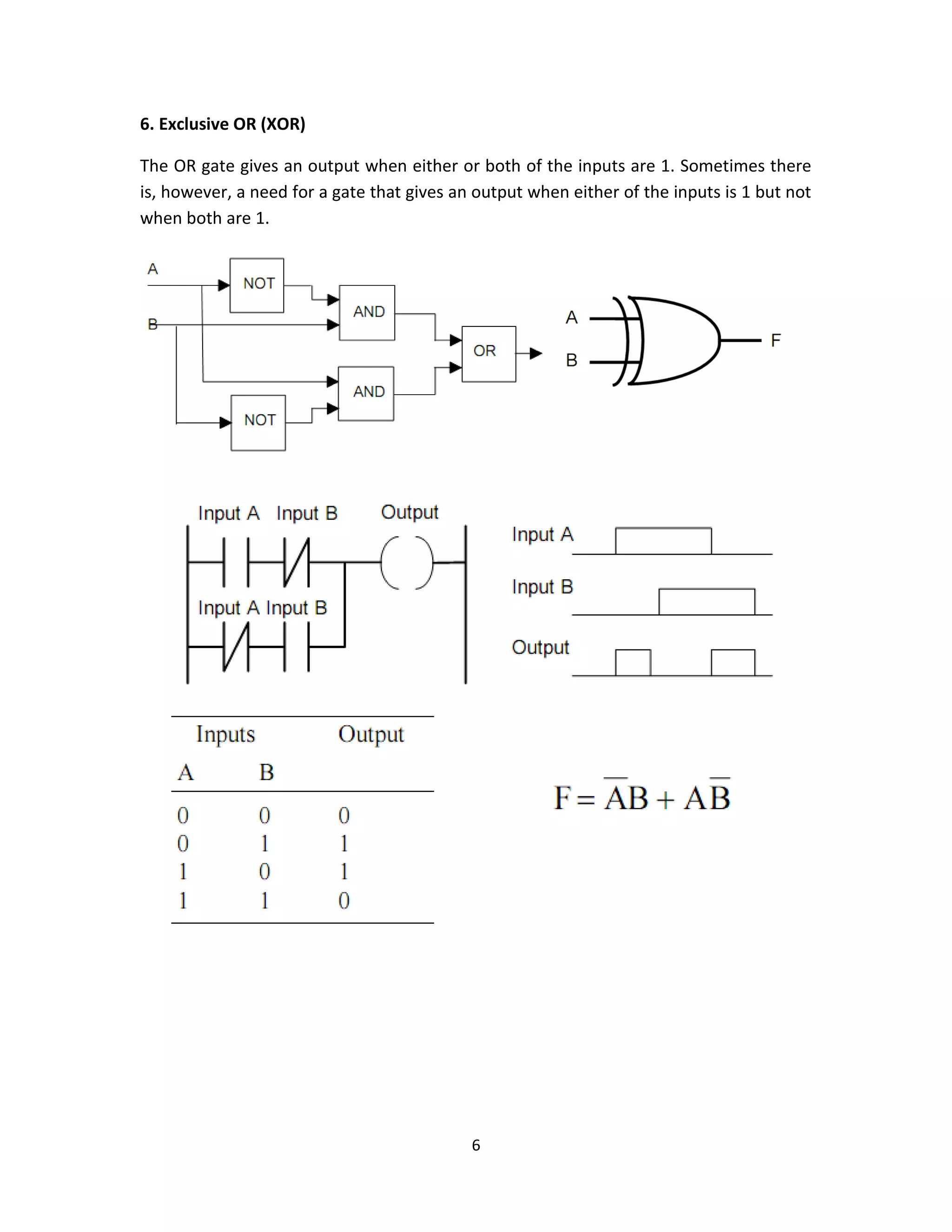
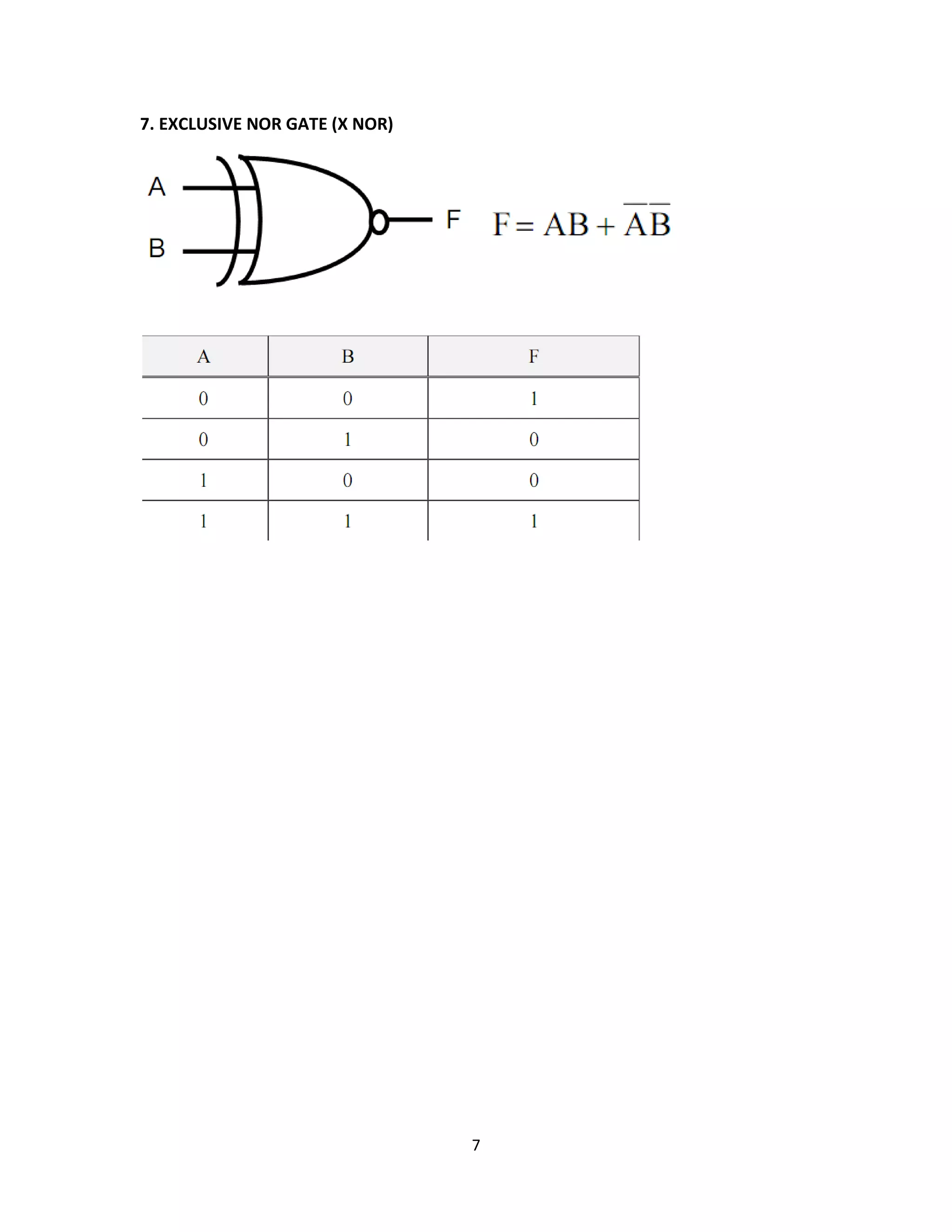
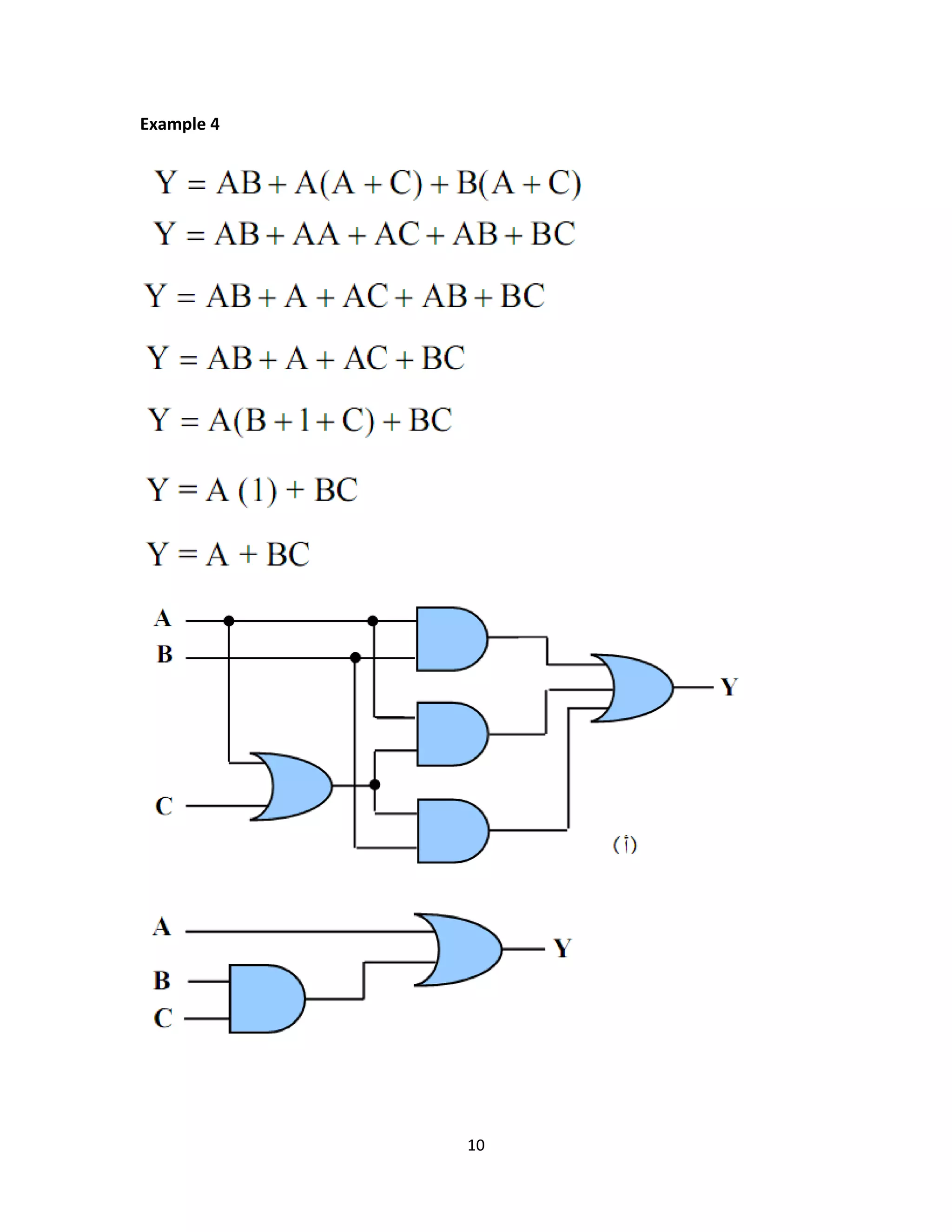
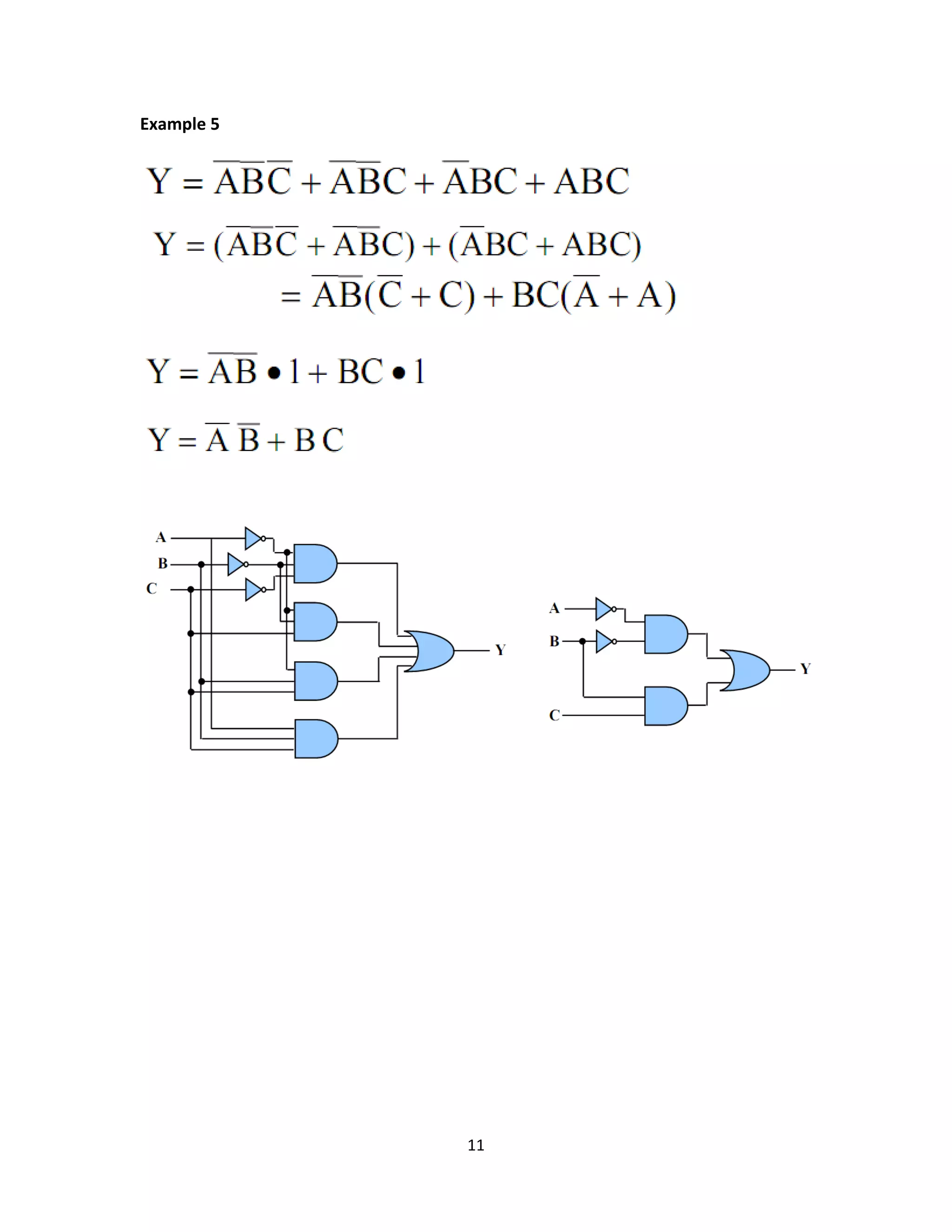
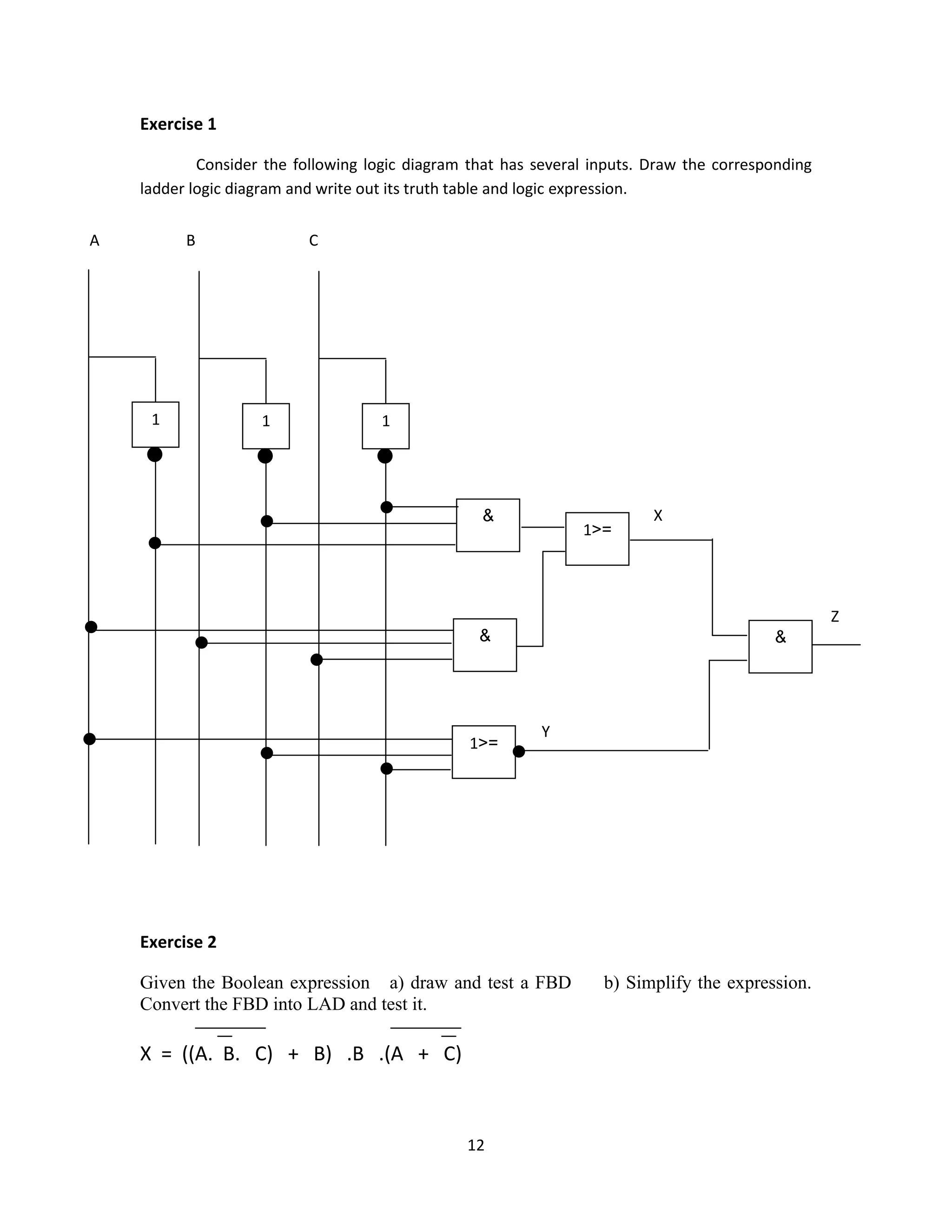
This document provides an overview of common logic circuits, including AND, OR, NOT, NAND, NOR, XOR, and XNOR gates, explaining their functions and giving practical examples. It also introduces Boolean algebra and offers exercises related to logic diagrams and truth tables. Additionally, it discusses simplifications and De Morgan's laws in the context of logic circuit design.

1. 1
___________________________________
3. LOGIC CIRCUITS
___________________________________
This chapter is a consideration of the common logic functions.
1. AND
Figure below shows a situation where an output is not energized unless two,
normally open, switches are both closed. Switch A and switch B have both to be
closed, which thus gives an AND logic situation.
Truth table
F = A & B F = A . B BAF  F=AB
An example of an AND gate is an interlock control system for a machine tool so that it
can only be operated when the safety guard is in position and the power switched on.

2. 2
1. OR
Figure below shows an electrical circuit where an output is energized when switch A or
B, both normally open, are closed. This describes an OR logic gate in that input A or
input B must be on for there to be an output.
Truth table
F = A OR B F = A + B BAF 
An example of an OR gate control system is a conveyor belt transporting bottled
products to packaging where a deflector plate is activated to deflect bottles into a
reject bin if either the weight is not within certain tolerances or there is no cap on the
bottle.

3. 3
3. NOT
Figure below shows an electrical circuit controlled by a switch that is normally closed.
When there is an input to the switch, it opens and there is then no current in the circuit.
This illustrates a NOT gate in that there is an output when there is no input and no
output when there is an input. The gate is sometimes referred to as an inverter.
An example of a NOT gate control system is a light that comes on when it becomes
dark, i.e. when there is no light input to the light sensor there is an output.

4. 4
4. NAND
Suppose we follow an AND gate with a NOT gate. The consequence of having the NOT
gate is to invert all the outputs from the AND gate. An alternative, which gives exactly
the same results, is to put a NOT gate on each input and then follow that with OR.
BAF 
An example of a NAND gate control system is a warning light that comes on if, with a
machine tool, the safety guard switch has not been activated and the limit switch
signaling the presence of the workpiece has not been activated.

5. 5
5. NOR
Suppose we follow an OR gate by a NOT gate. The consequence of having the NOT gate
is to invert the outputs of the OR gate. An alternative, which gives exactly the same
results, is to put a NOT gate on each input and then an AND gate for the resulting
inverted inputs.
BAF 

6. 6
6. Exclusive OR (XOR)
The OR gate gives an output when either or both of the inputs are 1. Sometimes there
is, however, a need for a gate that gives an output when either of the inputs is 1 but not
when both are 1.

7. 7
7. EXCLUSIVE NOR GATE (X NOR)

8. 8
Boolean algebra
ABBA
ABBA


CBACBA
CBACBA


)()(
)()(
)()()(
)()()(
CABACBA
CABACBA


De Morgan Laws:
BABA
BABA


)(
)(
Others:
AAA AA  0
0 AA11A
AA 00 A
ABAA  )(AA 1
BABAA  )(AAA 
)()()( CBACABA 1 AA

9. 9
SOLVED EXAMPLES (Simplifications)
Example 1
Example 2 Example 3

10. 10
Example 4

11. 11
Example 5

12. 12
Exercise 1
Consider the following logic diagram that has several inputs. Draw the corresponding
ladder logic diagram and write out its truth table and logic expression.
Exercise 2
Given the Boolean expression a) draw and test a FBD b) Simplify the expression.
Convert the FBD into LAD and test it.
X = ((A. B. C) + B) .B .(A + C)
1 1 1
&
1 =<
X
&
1 =<
&
Z
Y
A B C

13. 13
Exercise 3
Draw the output as a function of time if
A
t
B
t
Exercise 4
Considering the following logic equation:
(i) Draw the logic circuit for the above equation.
(ii) Deduce the truth table.
(iii) Simplify the above equation.
(iv) Write the truth table for the simplified equation.