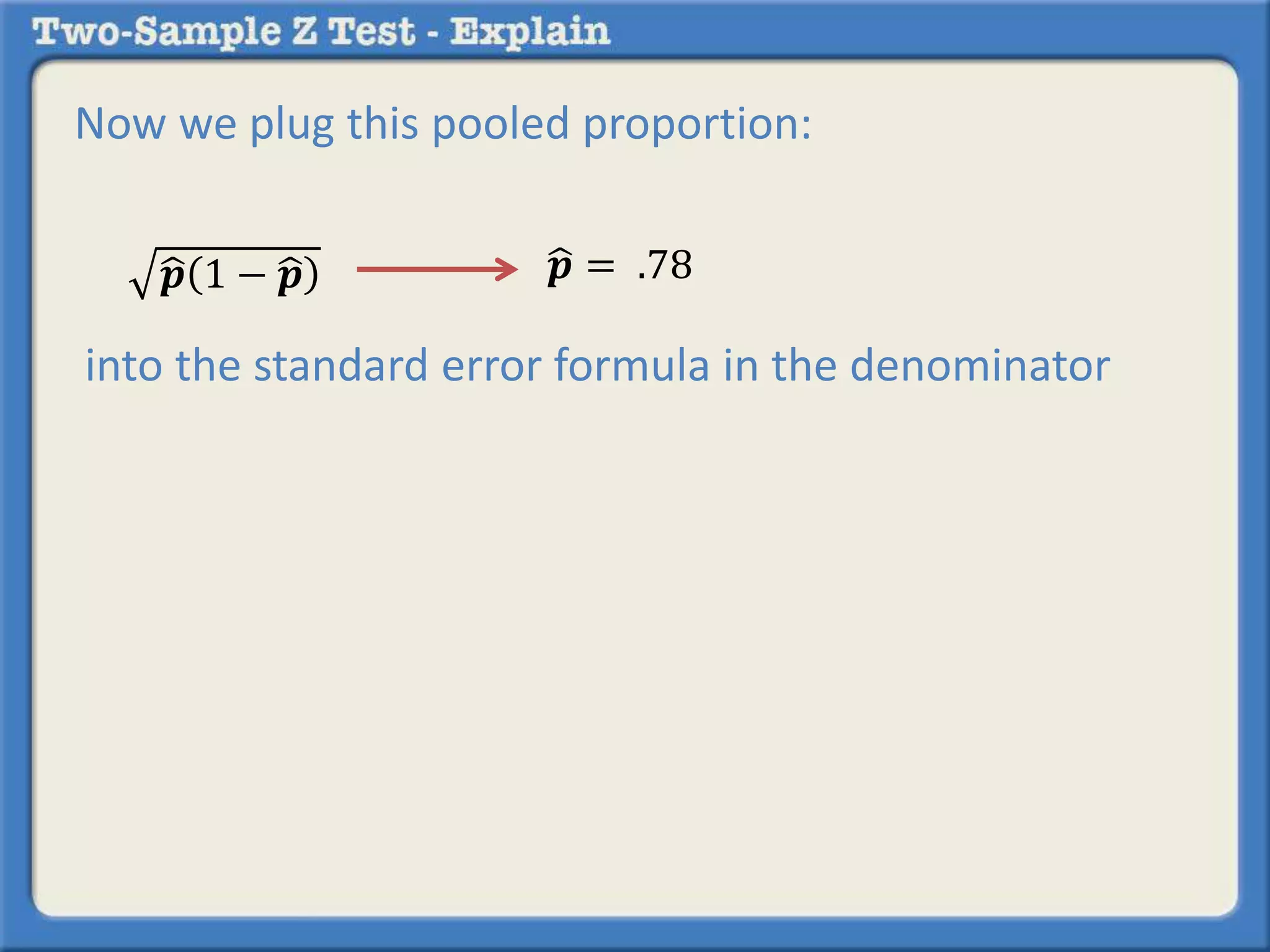
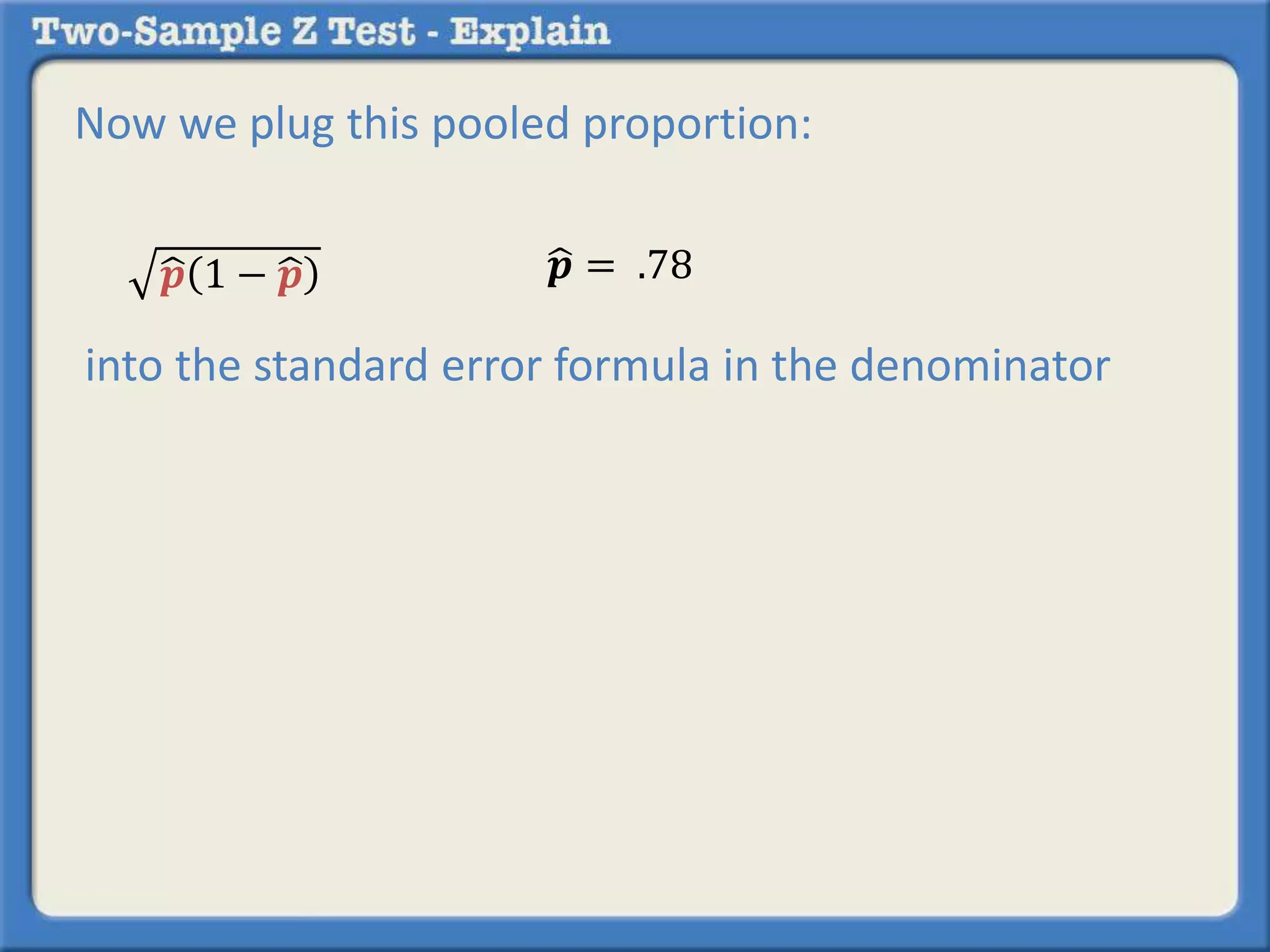
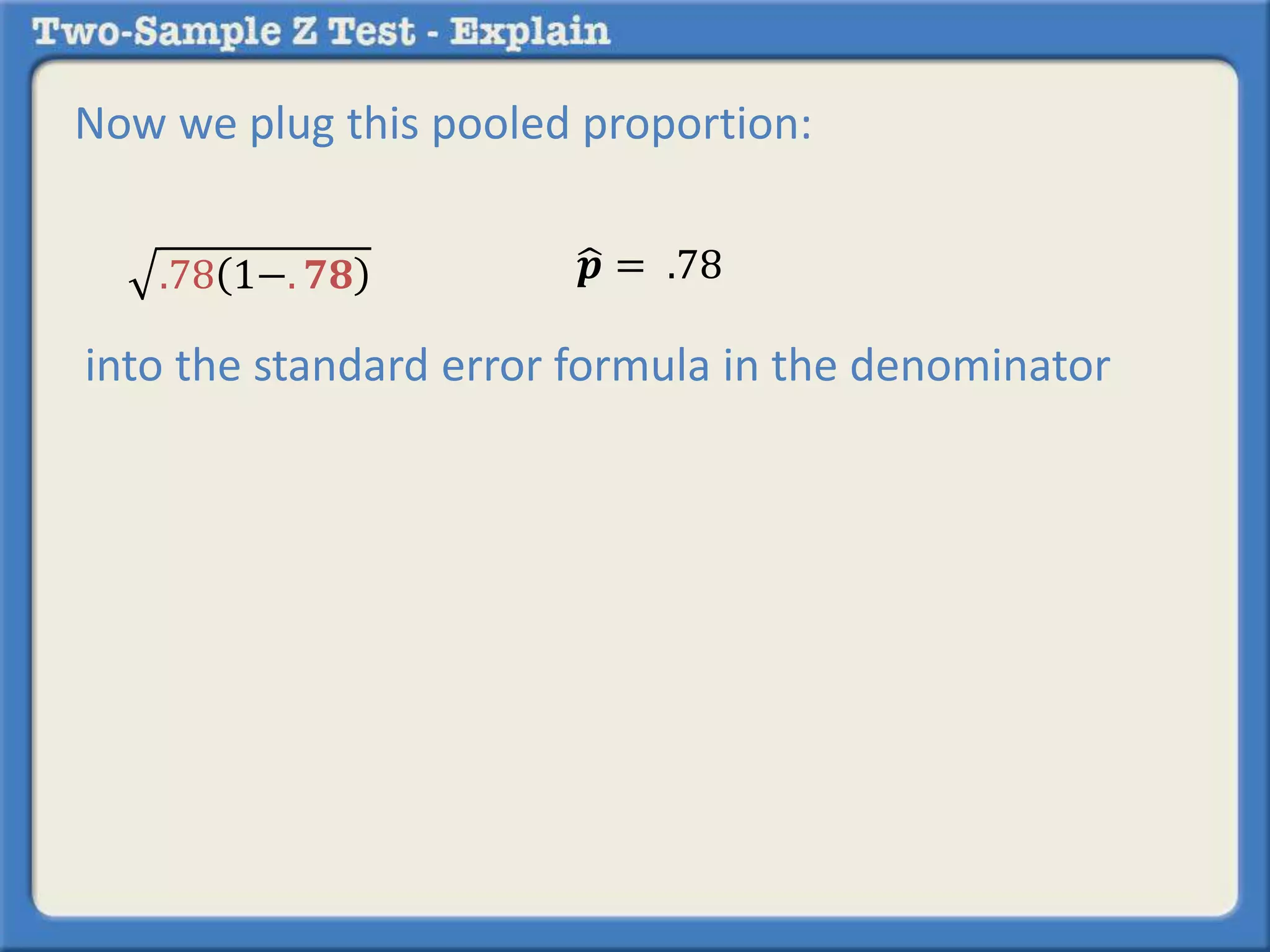
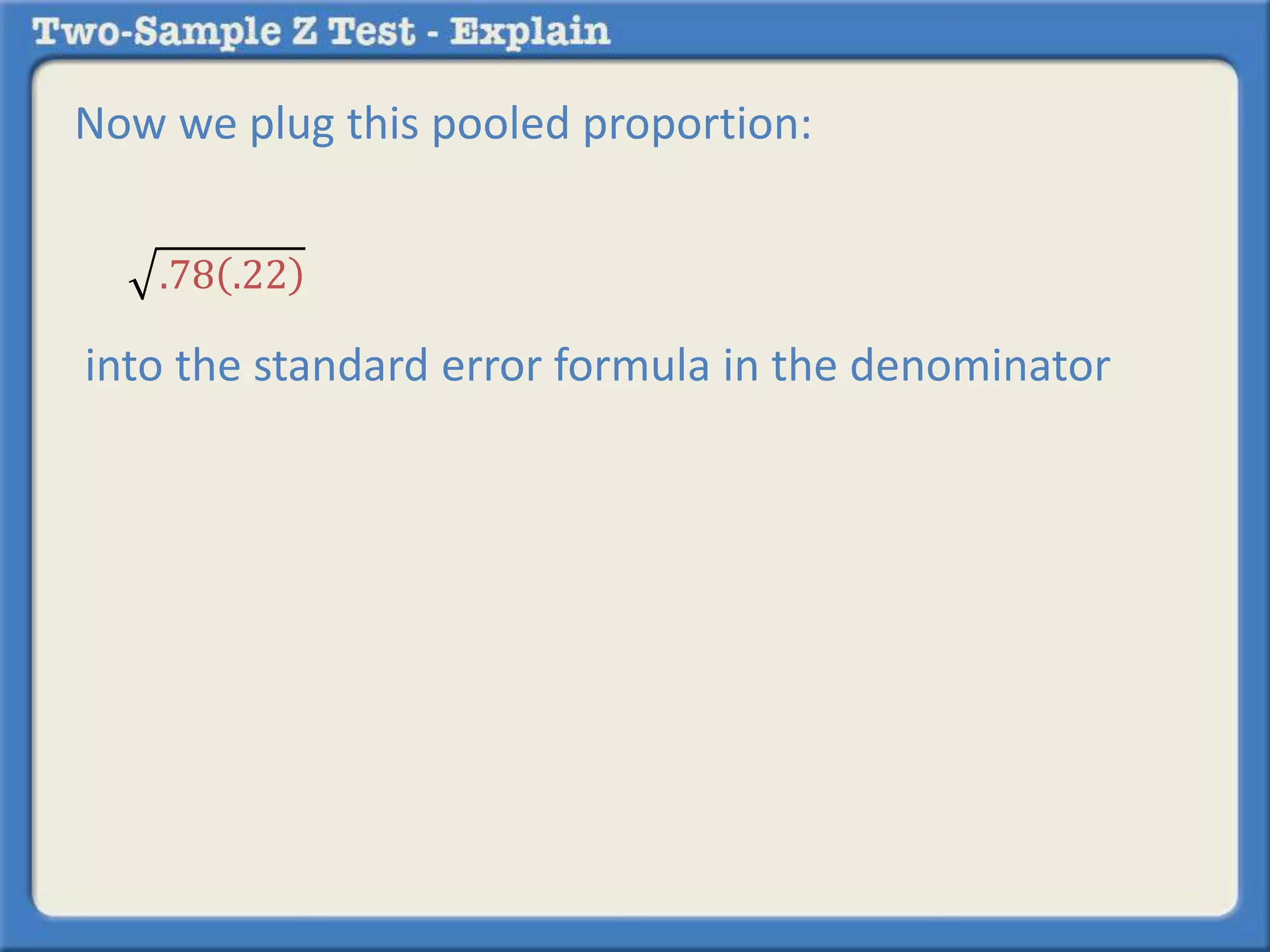
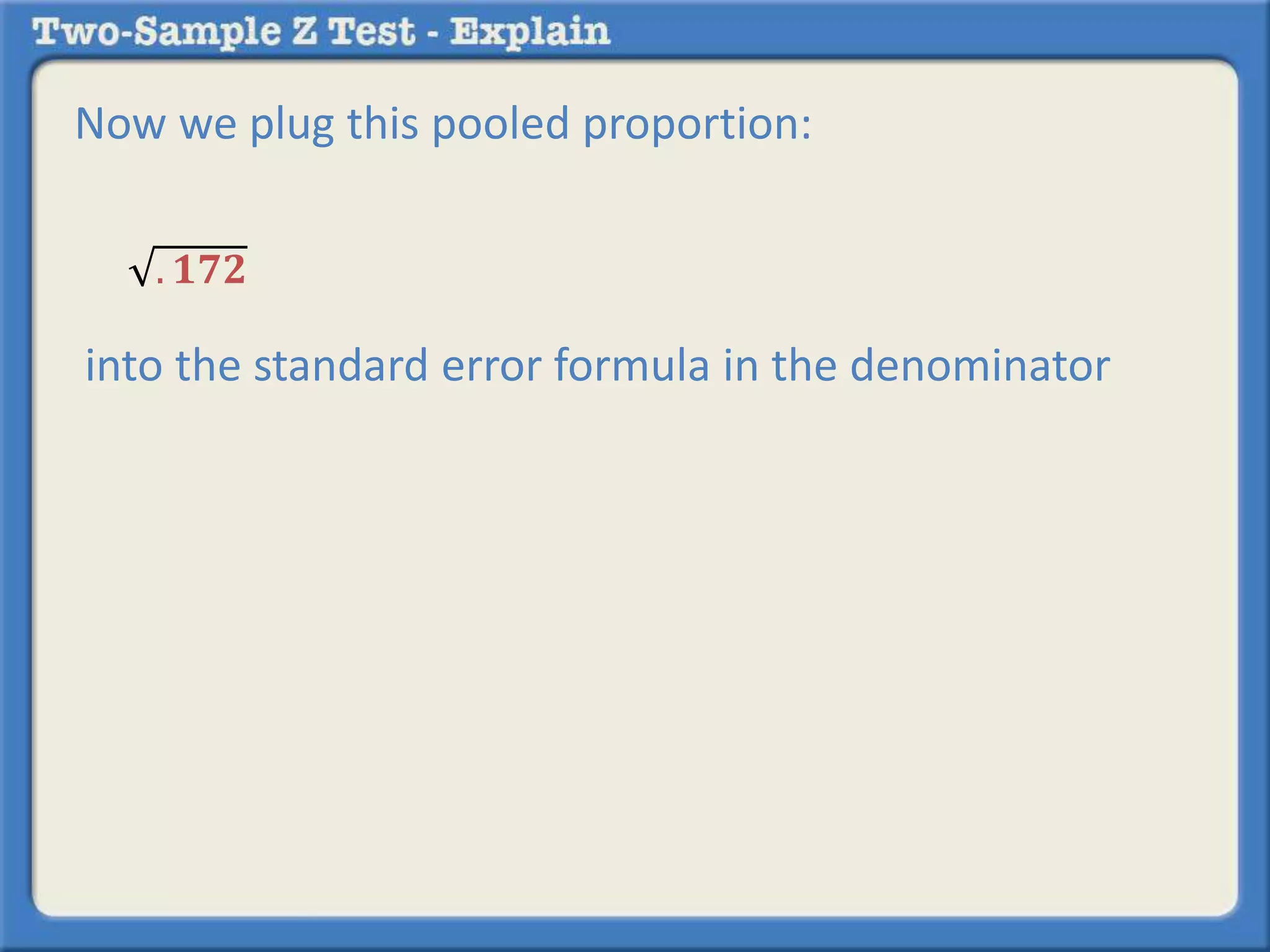
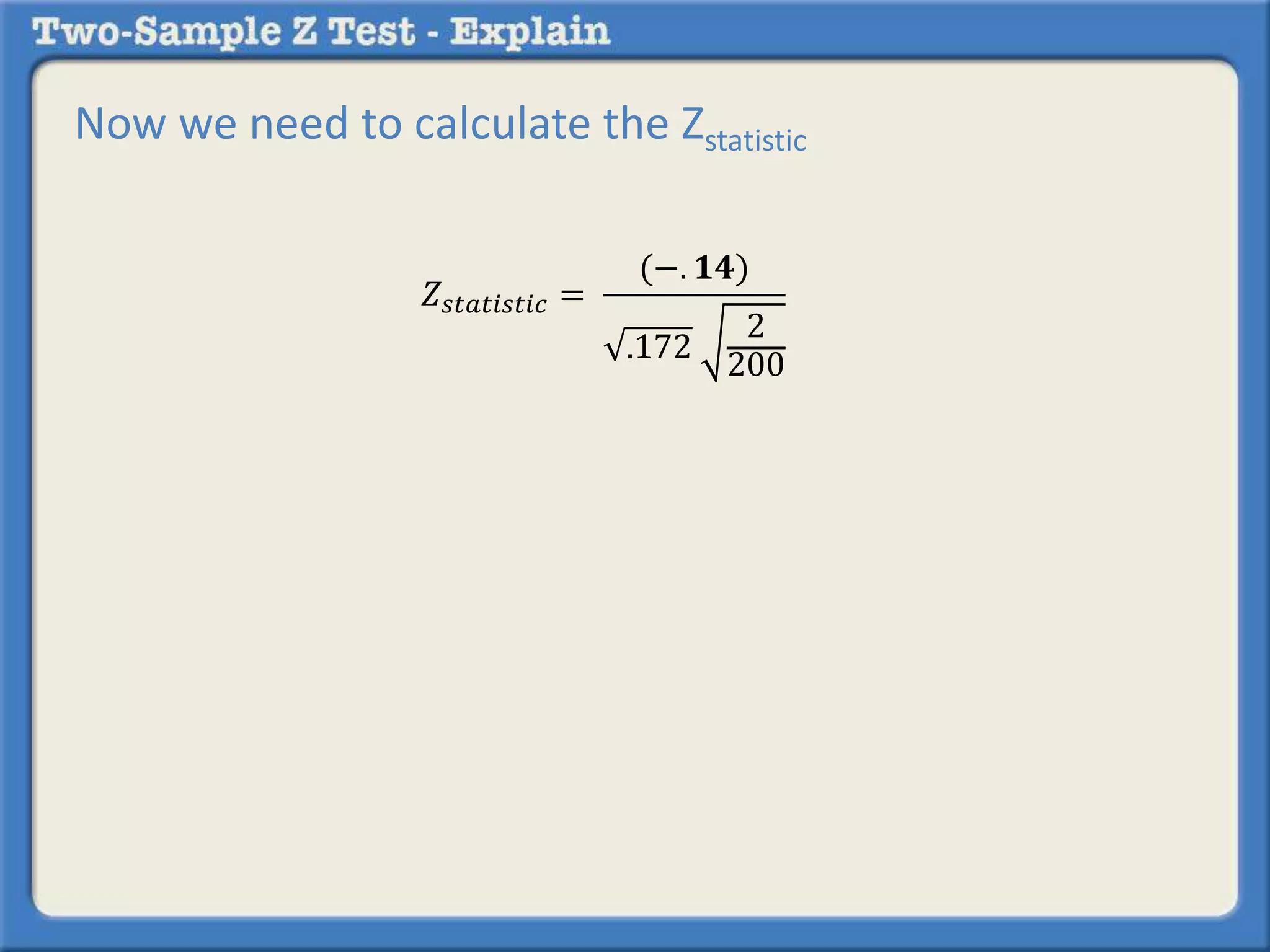
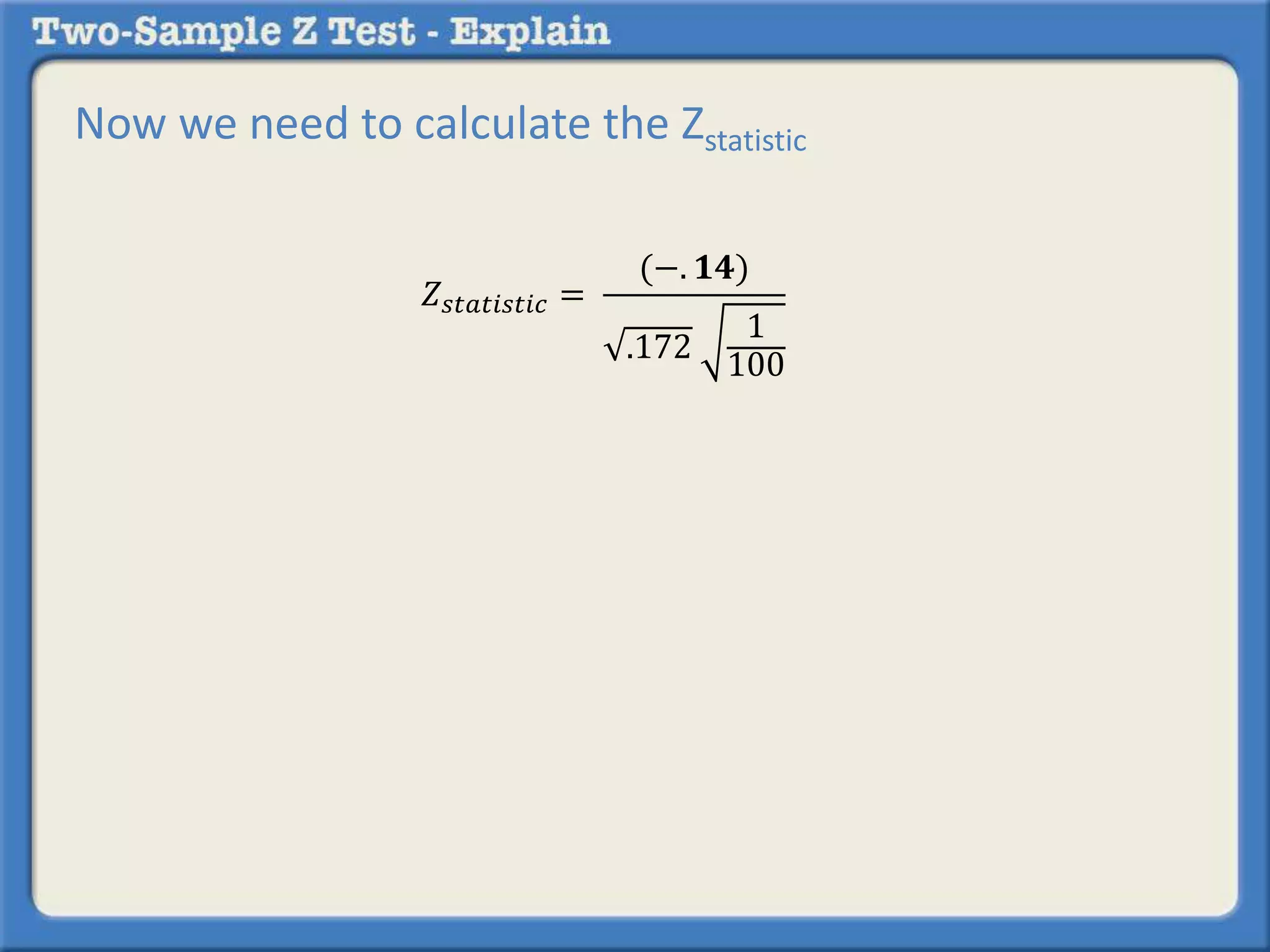
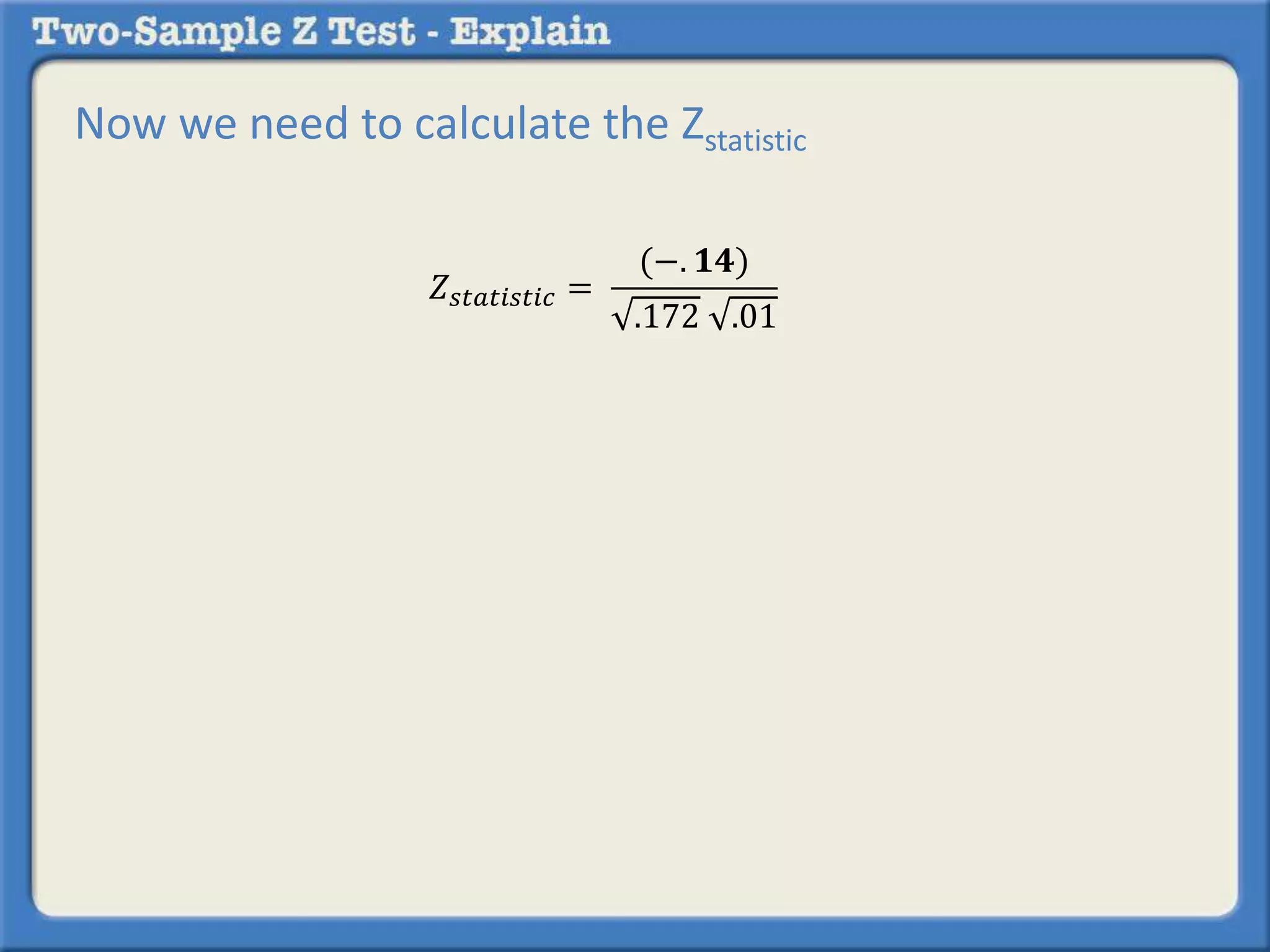
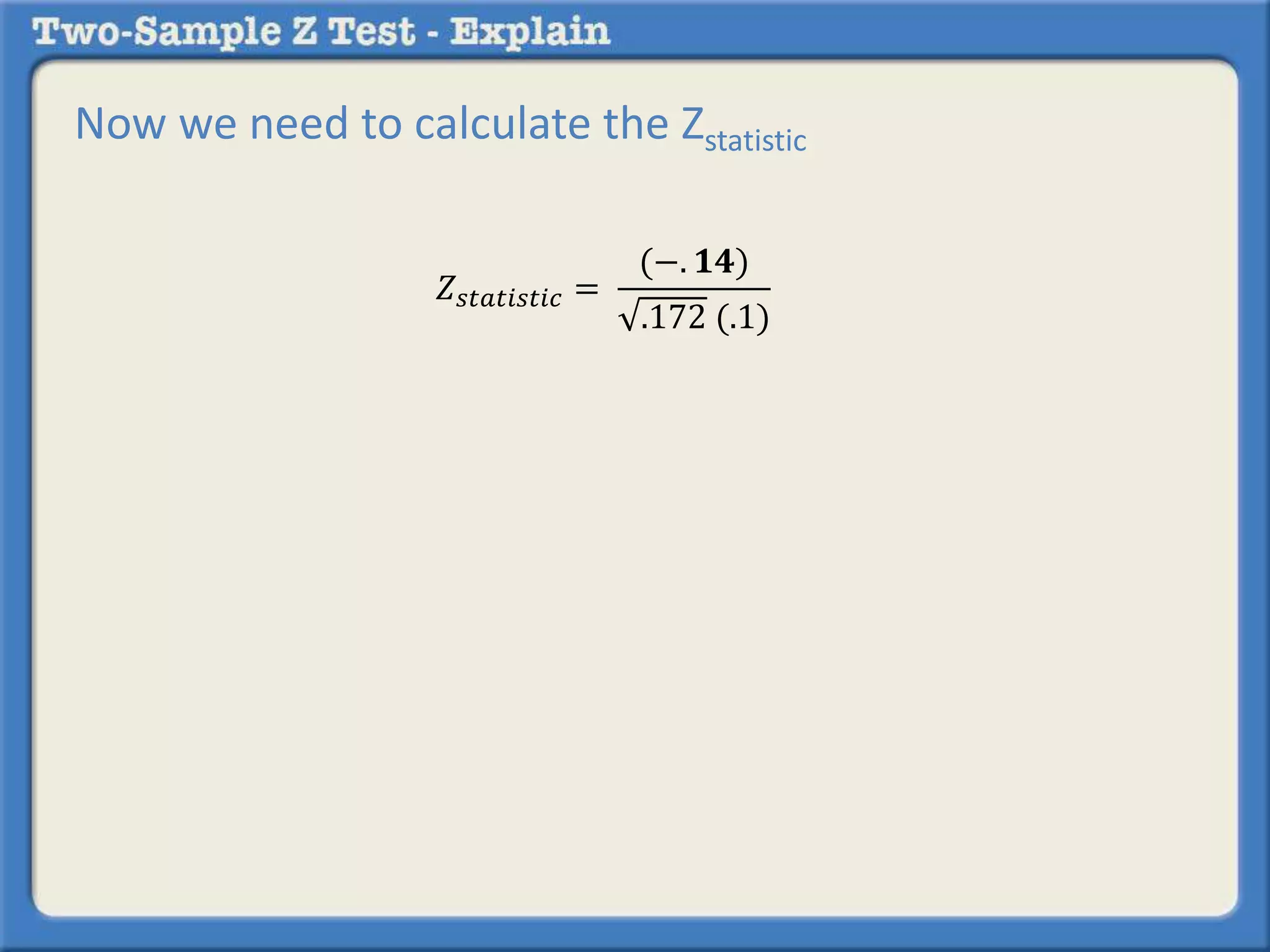
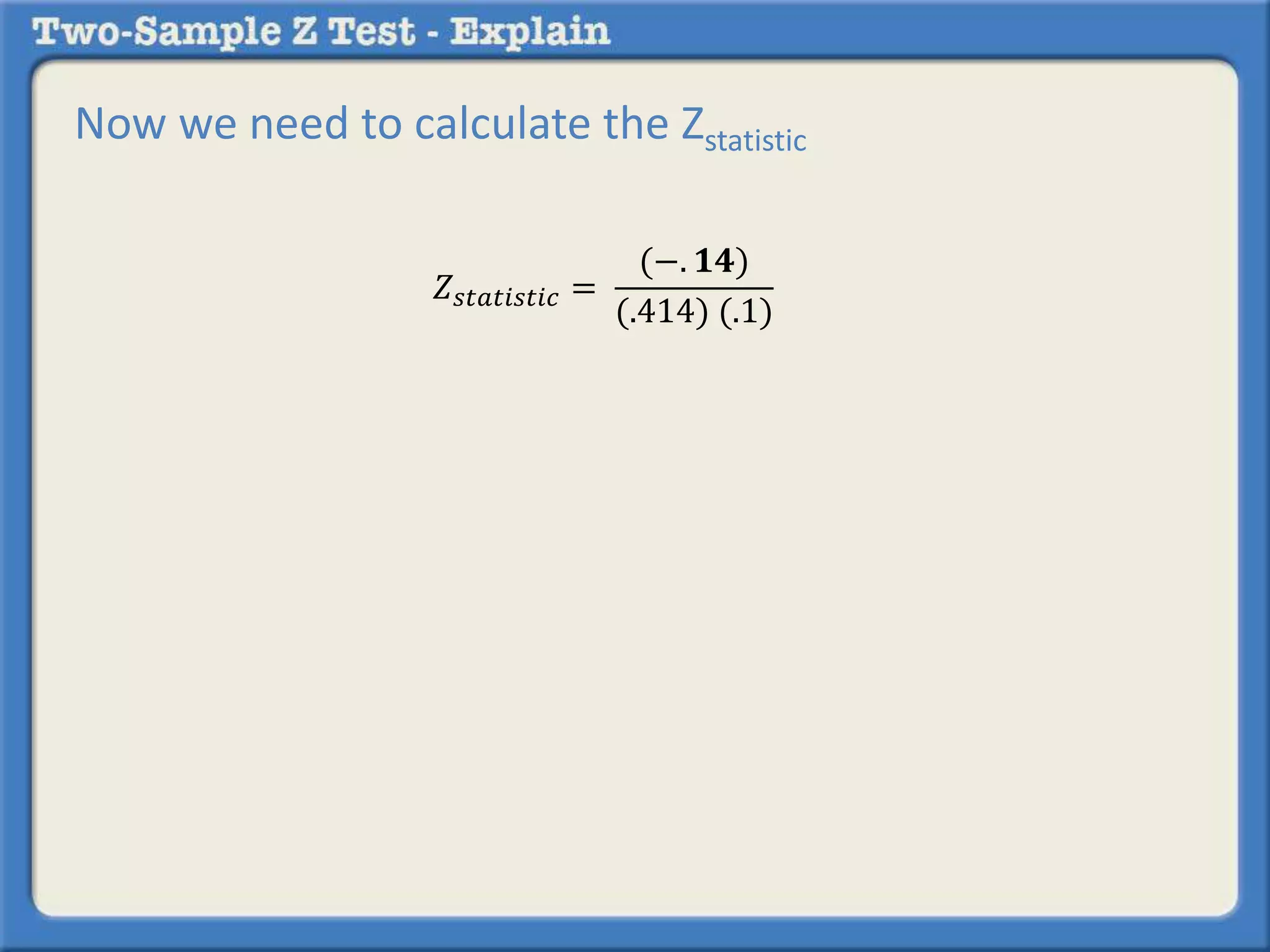
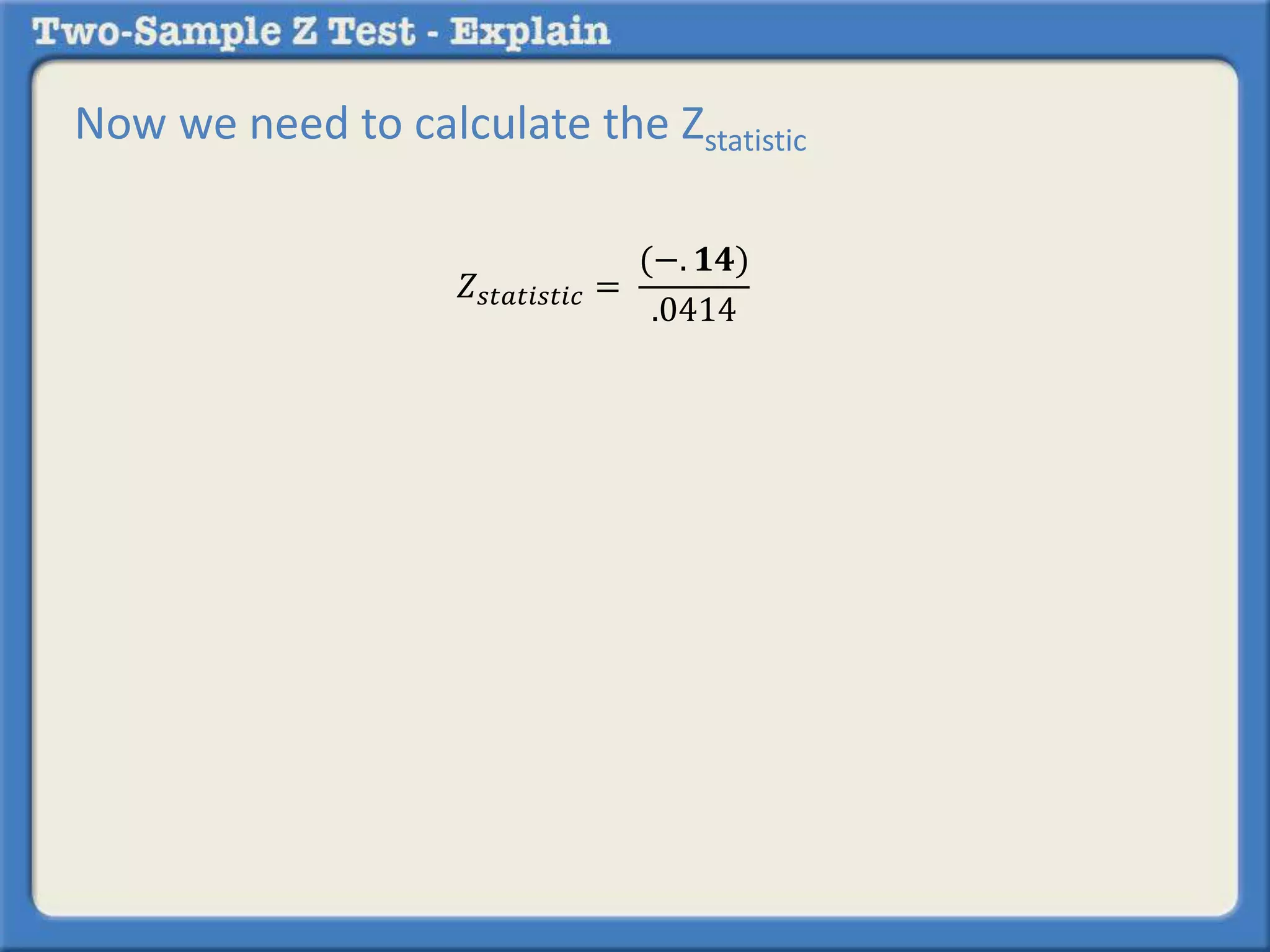
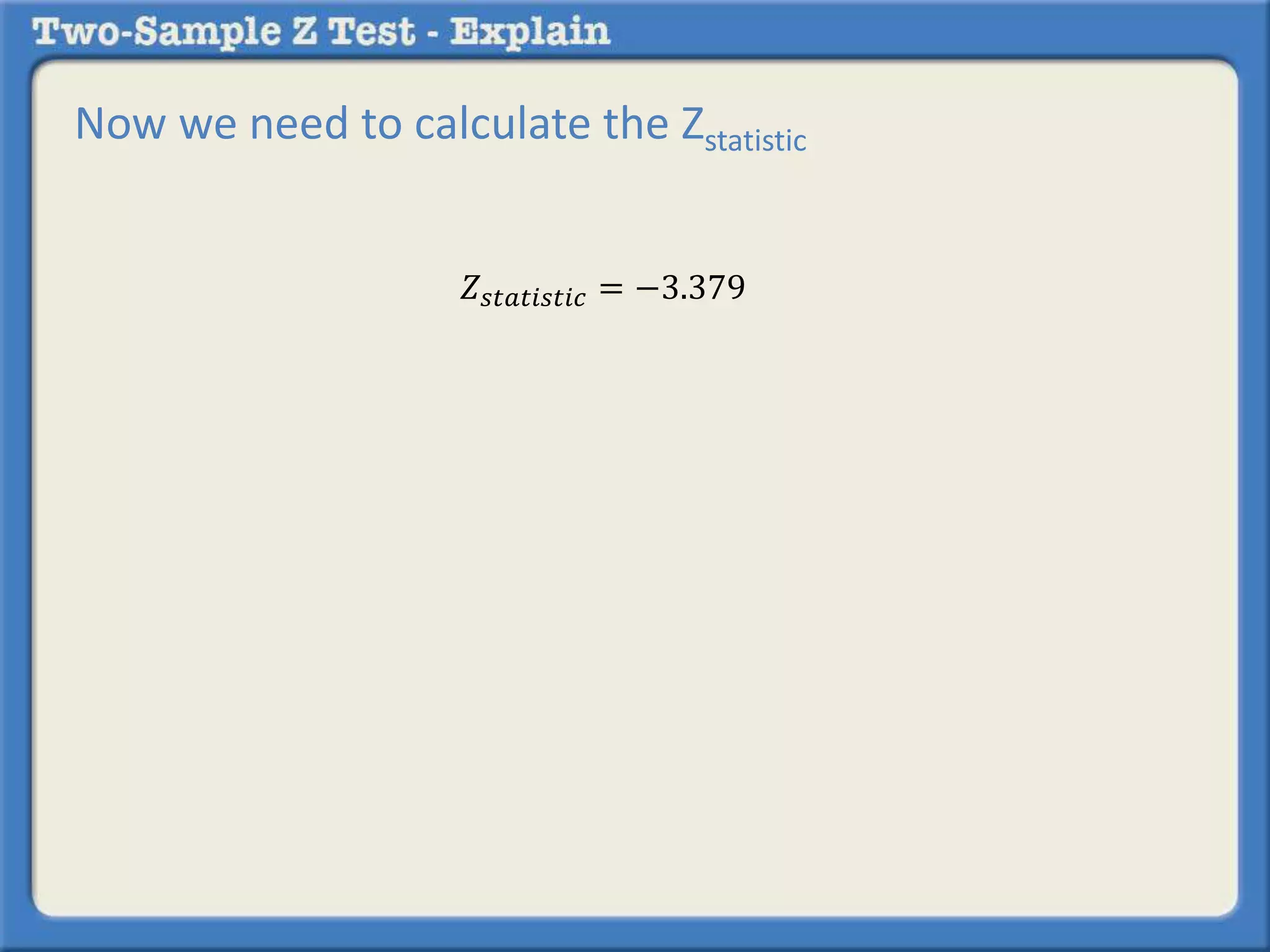
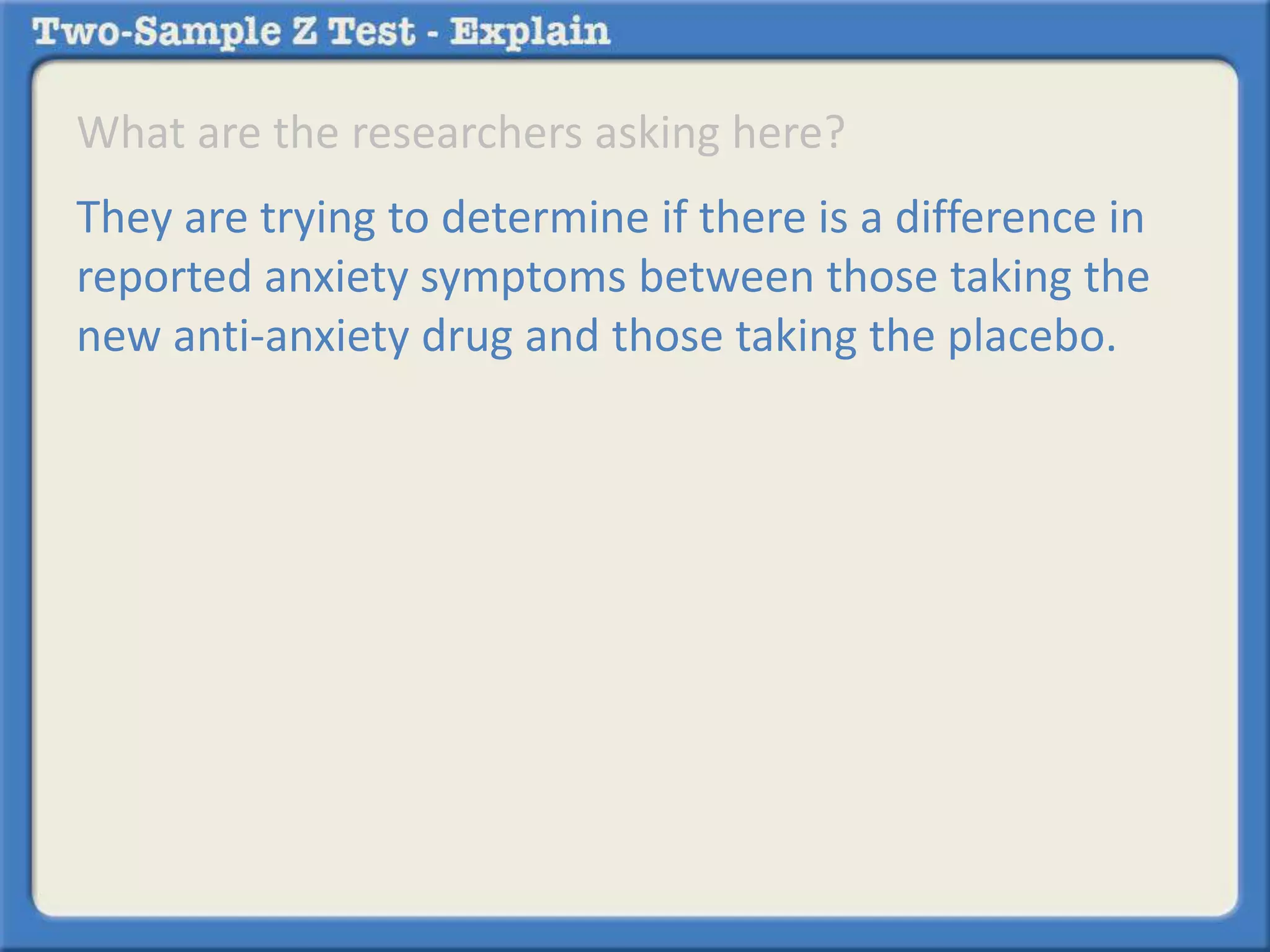
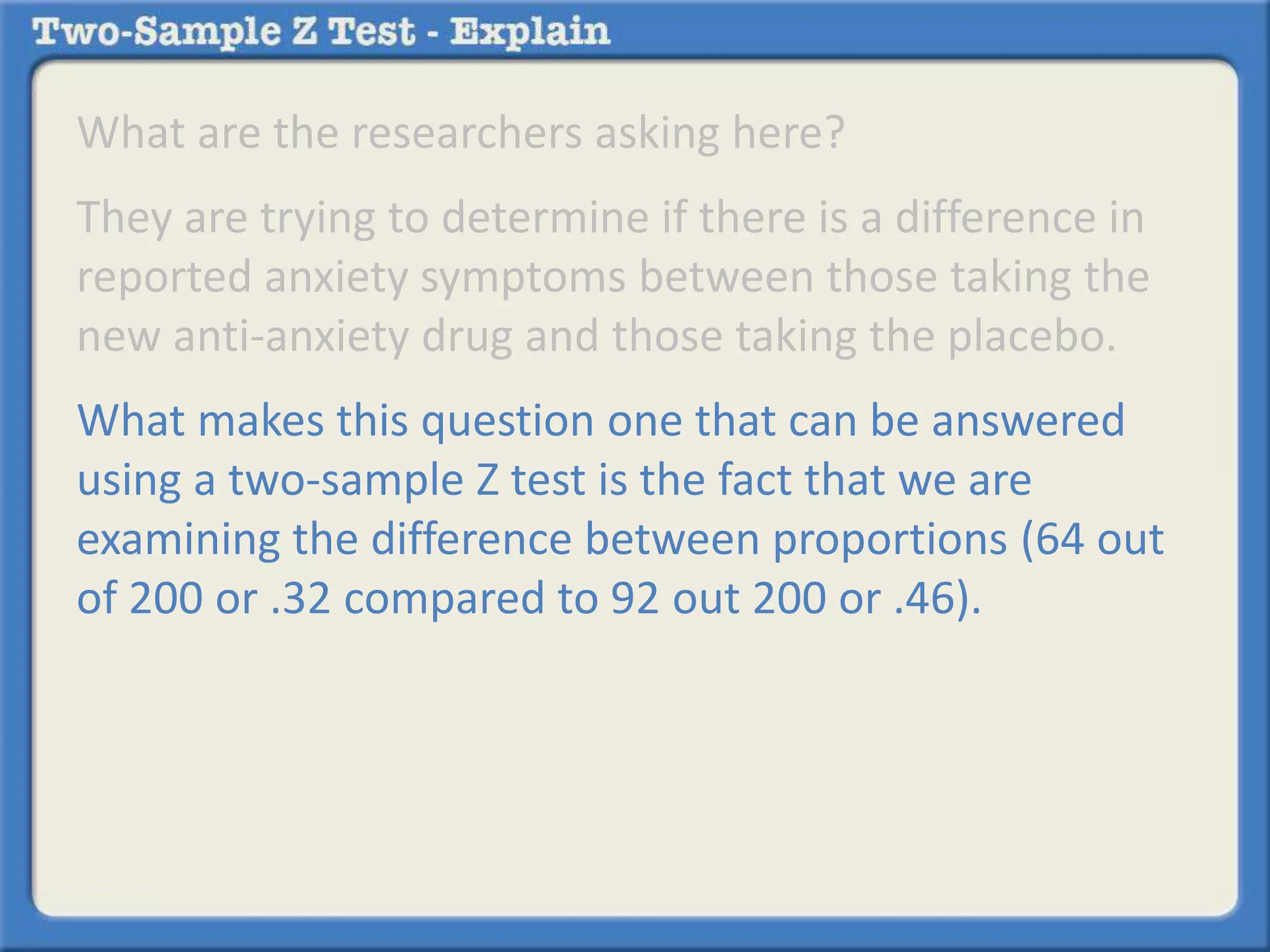
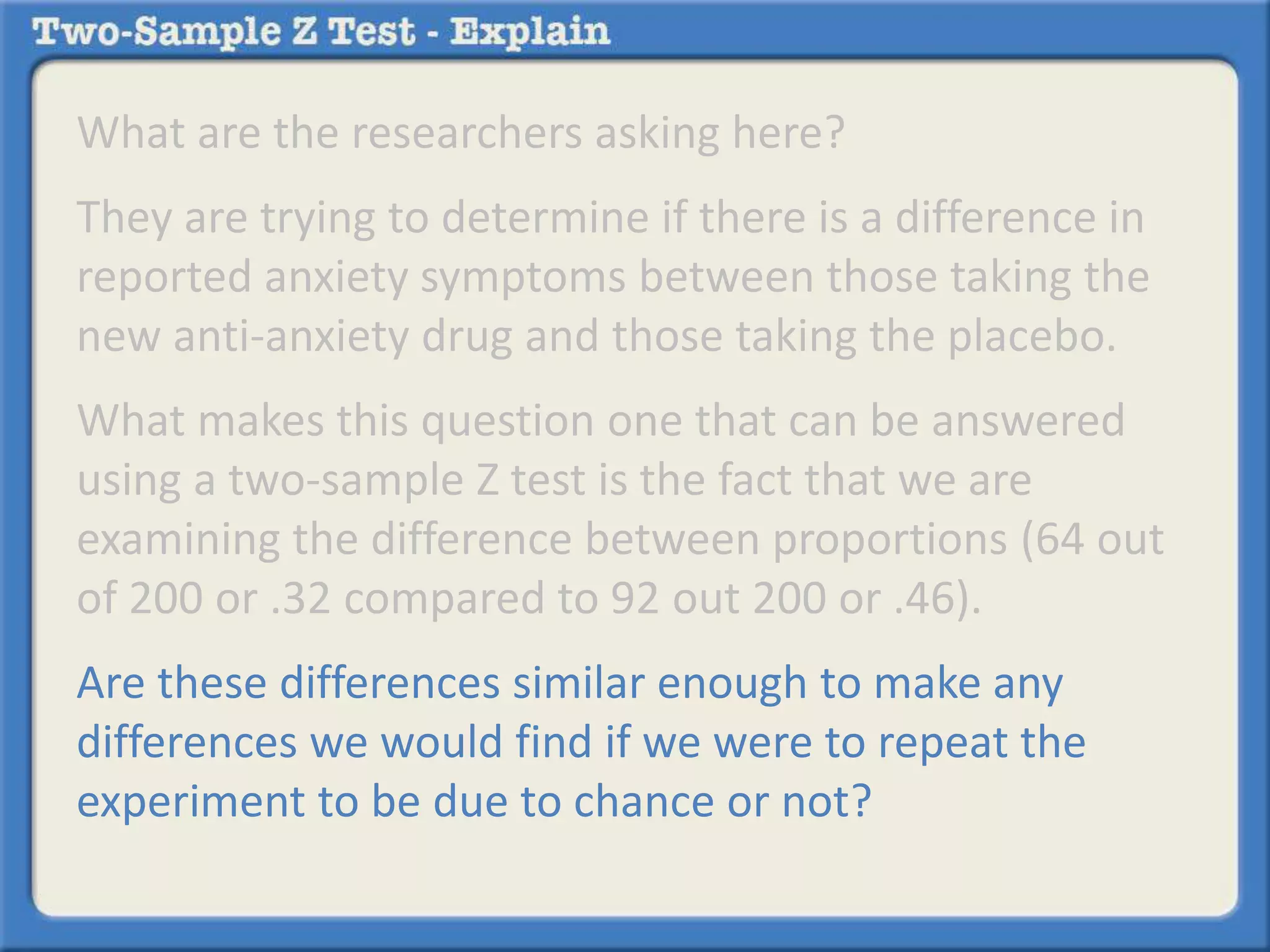
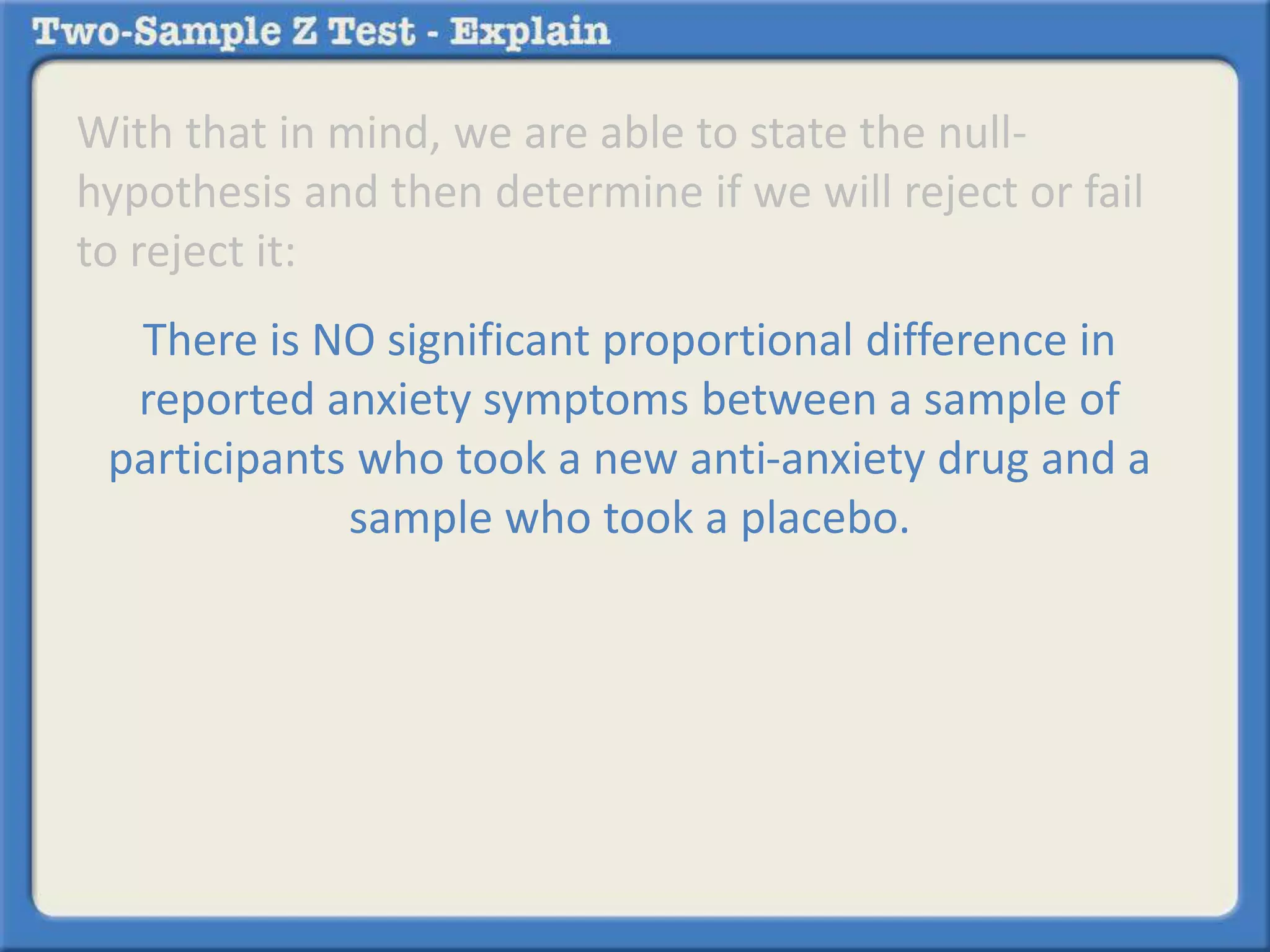
Researchers tested a new anti-anxiety medication on 200 people and a placebo on another 200 people. 64 of those on the medication and 92 of those on the placebo reported anxiety symptoms. The researchers want to determine if there is a statistically significant difference in reported anxiety between the two groups using a two-sample z-test with an alpha of 0.05. A two-sample z-test is used to compare differences between two sample proportions and determines if any observed difference is likely due to chance or not.

1. Two-Sample Z Test
Explanation

2. A two-sample Z test is used to compare the differences
statistically between two sample proportions.

3. A two-sample Z test is used to compare the differences
statistically between two sample proportions.
Consider the following question:

4. A two-sample Z test is used to compare the differences
statistically between two sample proportions.
Consider the following question:
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

5. What are the researchers asking here?

6. What are the researchers asking here?
They are trying to determine if there is a difference in
reported anxiety symptoms between those taking the
new anti-anxiety drug and those taking the placebo.

7. What are the researchers asking here?
They are trying to determine if there is a difference in
reported anxiety symptoms between those taking the
new anti-anxiety drug and those taking the placebo.
What makes this question one that can be answered
using a two-sample Z test is the fact that we are
examining the difference between proportions (64 out
of 200 or .32 compared to 92 out 200 or .46).

8. What are the researchers asking here?
They are trying to determine if there is a difference in
reported anxiety symptoms between those taking the
new anti-anxiety drug and those taking the placebo.
What makes this question one that can be answered
using a two-sample Z test is the fact that we are
examining the difference between proportions (64 out
of 200 or .32 compared to 92 out 200 or .46).
Are these differences similar enough to make any
differences we would find if we were to repeat the
experiment to be due to chance or not?

9. With that in mind, we are able to state the null-hypothesis
and then determine if we will reject or fail
to reject it:

10. With that in mind, we are able to state the null-hypothesis
and then determine if we will reject or fail
to reject it:
There is NO significant proportional difference in
reported anxiety symptoms between a sample of
participants who took a new anti-anxiety drug and a
sample who took a placebo.

11. Since the test uses a .05 alpha value, that is what we
will use to determine if the probability of a meaningful
difference is rare or common.

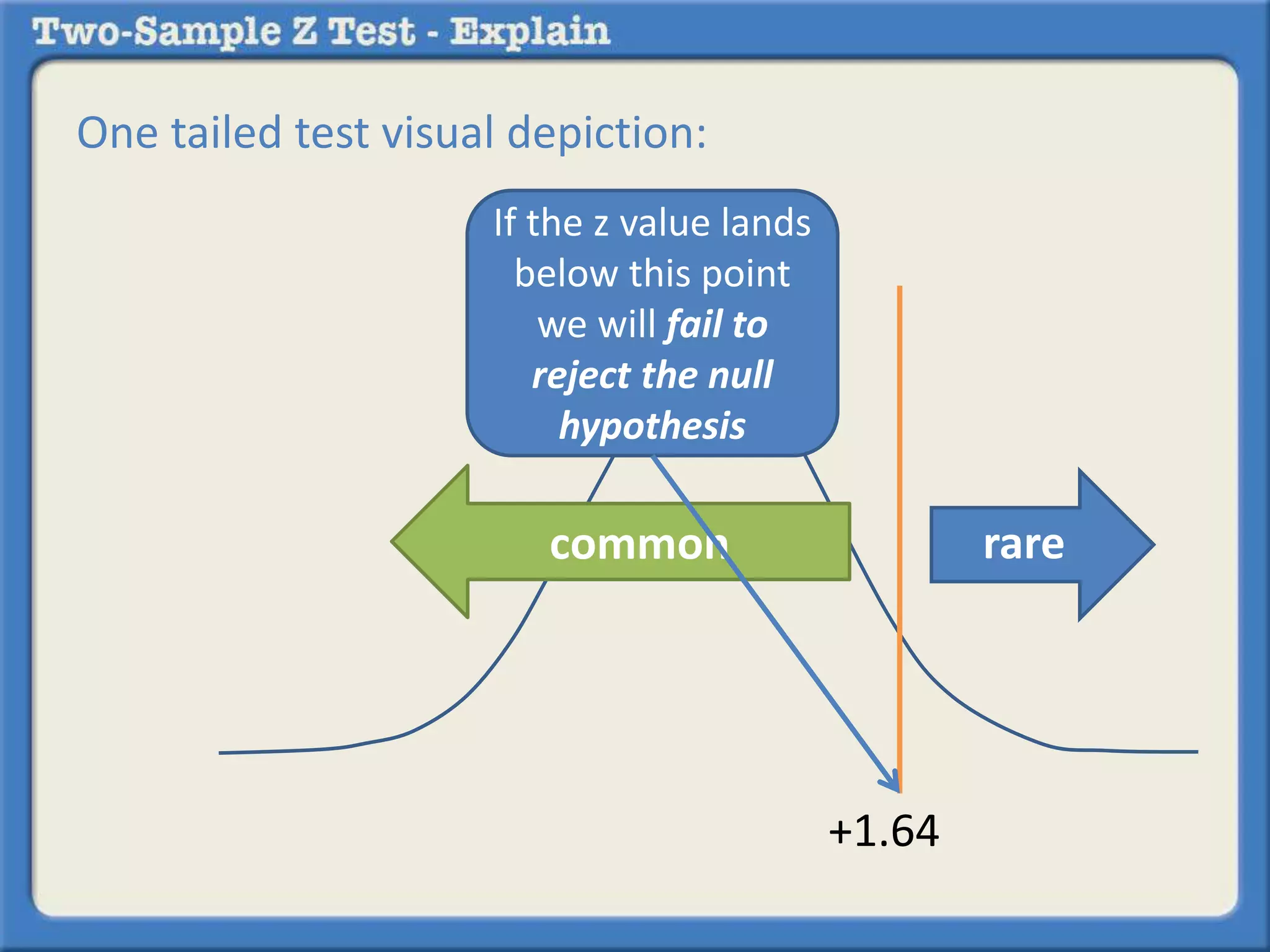
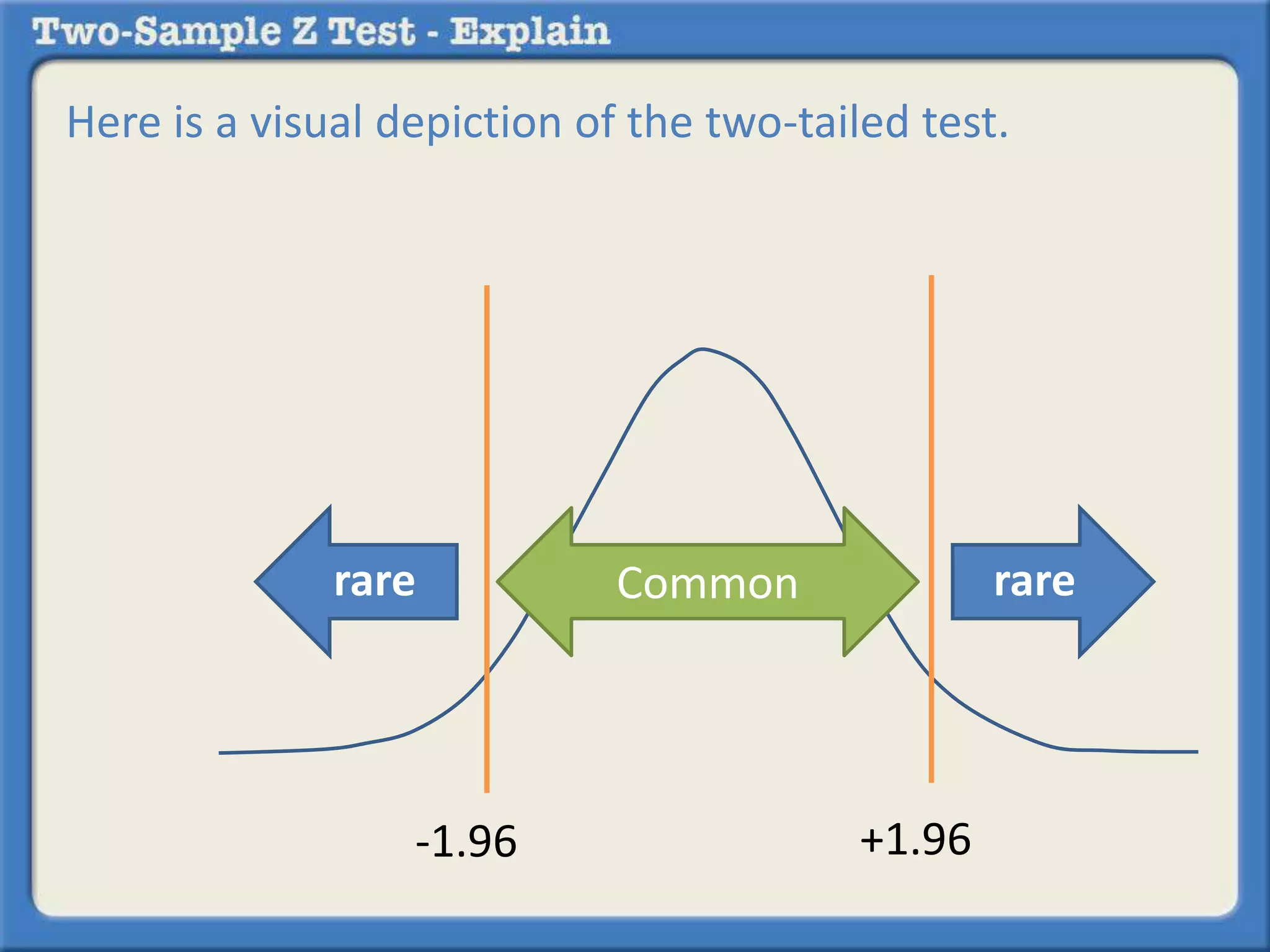
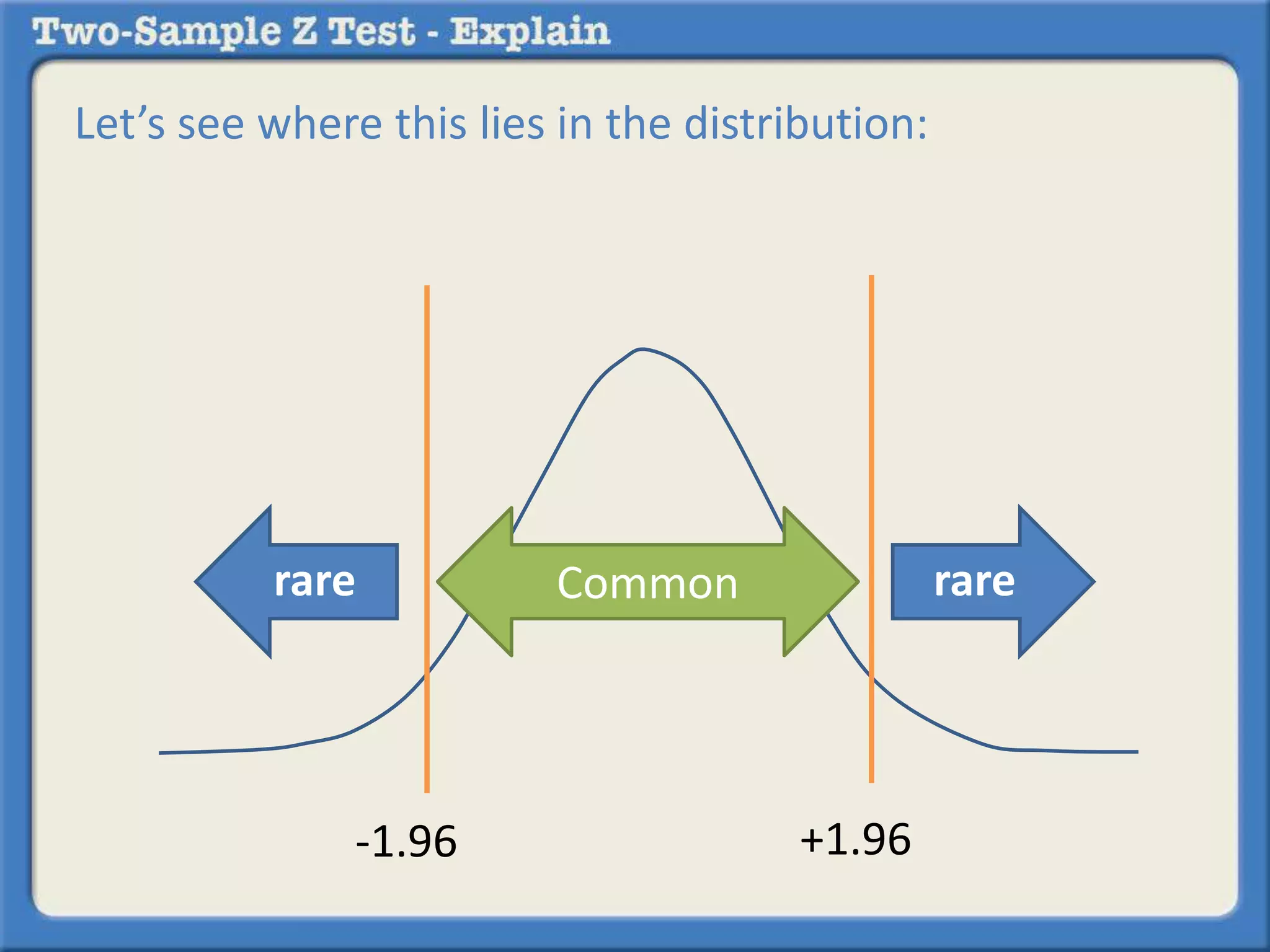
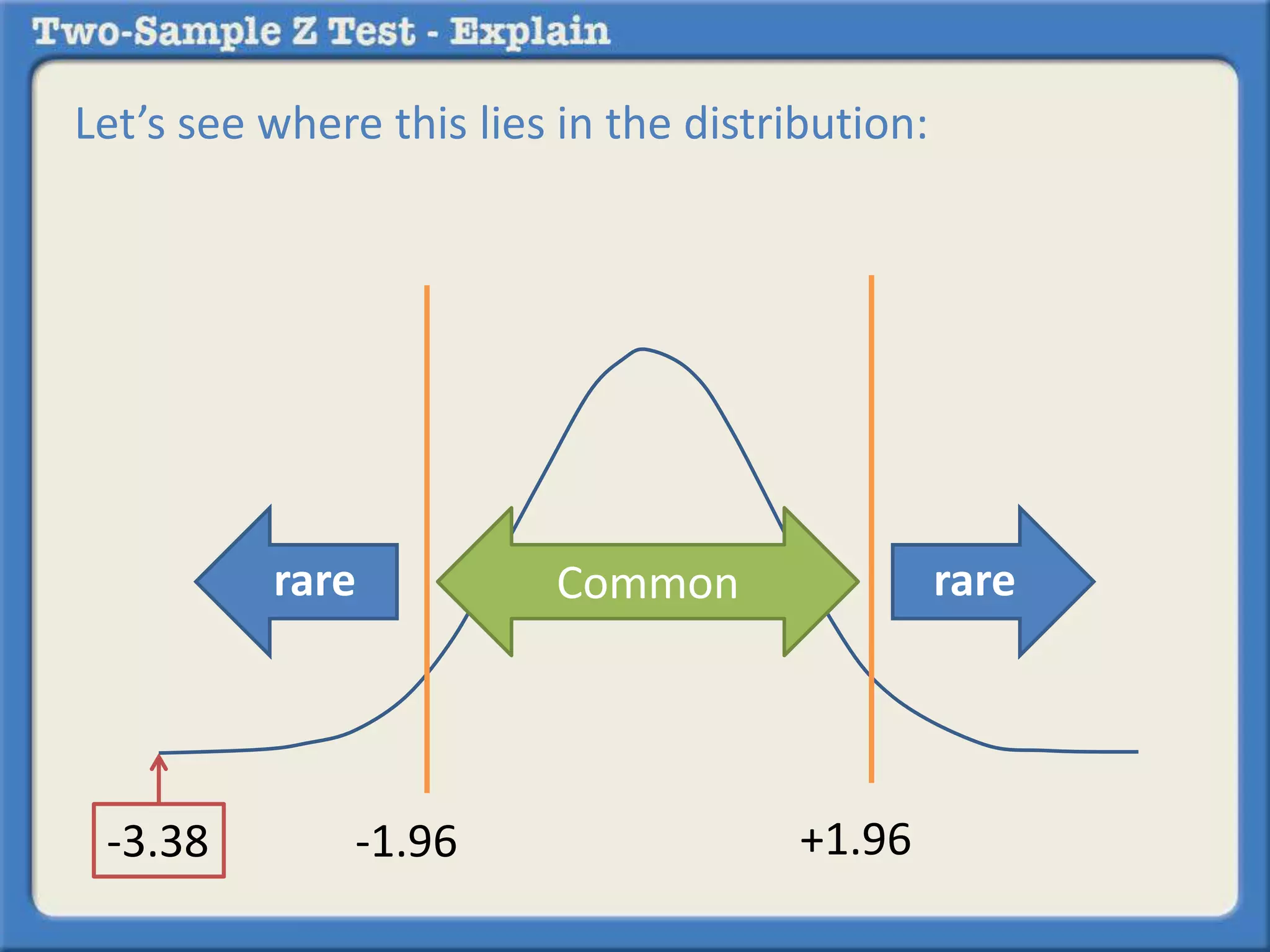
12. Since the test uses a .05 alpha value, that is what we
will use to determine if the probability of a meaningful
difference is rare or common.
The alpha value makes it possible to determine what is
called the z critical. If the z statistic that we are about
to calculate from the data in the question is outside of
the z critical [for a one-tailed test (e.g., +1.64) or a two-tailed
test (e.g., -1.96 or +1.96]

13. One tailed test visual depiction:
If the z value we
are about to
calculate lands
above this point,
we will reject the
null hypothesis
common rare
+1.64

14. One tailed test visual depiction:
common rare
+1.64
If the z value lands
below this point
we will fail to
reject the null
hypothesis

15. A one tailed test could also go the other direction if we
are testing the probability of one sample having a
smaller proportion than another.
rare common
-1.64

16. A two-tailed test implies that we are not sure as to
which direction it will go. We don’t know if the
placebo or the new anxiety medicine will have better
results.

17. Here is a visual depiction of the two-tailed test.
rare
-1.96
Common rare
+1.96

18. All we have left to do now is calculate the z statistic.

19. All we have left to do now is calculate the z statistic.
Here is the formula for the z statistic for a Two-Sample
Z-Test:
풁풔풕풂풕풊풔풕풊풄 =
(푝 1 − 푝 2)
푝 1 − 푝
1
푛1
+
1
푛2

20. In the numerator we are subtracting one sample
proportion from another sample proportion:
풁풔풕풂풕풊풔풕풊풄 =
(푝 1 − 푝 2)
푝 1 − 푝
1
푛1
+
1
푛2

21. In the numerator we are subtracting one sample
proportion from another sample proportion:
풁풔풕풂풕풊풔풕풊풄 =
(푝 1 − 푝 2)
푝 1 − 푝
1
푛1
+
1
푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

22. In the numerator we are subtracting one sample
proportion from another sample proportion:
풁풔풕풂풕풊풔풕풊풄 =
(푝 1 − 푝 2)
푝 1 − 푝
1
푛1
+
1
푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

23. In the numerator we are subtracting one sample
proportion from another sample proportion:
풁풔풕풂풕풊풔풕풊풄 =
(푝 1 − 푝 2)
푝 1 − 푝
1
푛1
+
1
푛2
92/200=.46
64/200=.32
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

24. In the numerator we are subtracting one sample
proportion from another sample proportion:
풁풔풕풂풕풊풔풕풊풄 =
(.32 − .46)
푝 1 − 푝
1
푛1
+
1
푛2
92/200=.46
64/200=.32
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

25. In the numerator we are subtracting one sample
proportion from another sample proportion:
풁풔풕풂풕풊풔풕풊풄 =
(−. ퟏퟐ)
푝 1 − 푝
1
푛1
+
1
푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

26. The denominator is the estimated standard error:
풁풔풕풂풕풊풔풕풊풄 =
(−.12)
푝 1 − 푝
1
푛1
+
1
푛2
This proportion is
called the pooled
standard deviation.
It is the same value
we use with
independent
sample t-tests.
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

27. The denominator is the estimated standard error:
풁풔풕풂풕풊풔풕풊풄 =
(−.12)
푝 1 − 푝
1
푛1
+
1
푛2
It is interesting to note that when you multiply a
proportion (.80) by its complement (1-.8 = .20)
you get the variance (.80*.20 = .16).
If you square that amount it comes to .04 and that
is the standard deviation.

28. Why is this important? Because the standard deviation
divided by the square root of the sample size is the
standard error.
풁풔풕풂풕풊풔풕풊풄 =
(−.12)
푝 1 − 푝
1
푛1
+
1
푛2
It is interesting to note that when you multiply a
proportion (.80) by its complement (1-.8 = .20)
you get the variance (.80*.20 = .16).
If you square that amount it comes to .04 and that
is the standard deviation.

29. And the larger the standard error the less likely the two
groups will be statistically significantly different.
풁풔풕풂풕풊풔풕풊풄 =
(−.12)
푝 1 − 푝
1
푛1
+
1
푛2
It is interesting to note that when you multiply a
proportion (.80) by its complement (1-.8 = .20)
you get the variance (.80*.20 = .16).
If you square that amount it comes to .04 and that
is the standard deviation.

30. Conversely, the smaller the standard error the more
likely the two groups will be statistically significantly
different.
풁풔풕풂풕풊풔풕풊풄 =
(−.12)
푝 1 − 푝
1
푛1
+
1
푛2
It is interesting to note that when you multiply a
proportion (.80) by its complement (1-.8 = .20)
you get the variance (.80*.20 = .16).
If you square that amount it comes to .04 and that
is the standard deviation.

31. So, let’s compute the pooled standard deviation:
풑 1 − 풑

32. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
푥1 + 푥2
푛1 + 푛2

33. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
푥1 + 푥2
푛1 + 푛2
Here’s the problem again:
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

34. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
푥1 + 푥2
푛1 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

35. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 푥2
푛1 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

36. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 푥2
푛1 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

37. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 푥2
200 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

38. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 푥2
200 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

39. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 92
200 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

40. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 92
200 + 푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

41. So, let’s compute the pooled standard deviation:
풑 1 − 풑 풑 =
64 + 92
200 + 200
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

42. Add the fractions:
풑 1 − 풑 풑 =
64 + 92
200 + 200

43. Add the fractions:
풑 1 − 풑 풑 =
156
200 + 200

44. Add the fractions:
풑 1 − 풑 풑 =
156
200 + 200

45. Add the fractions:
풑 1 − 풑 풑 =
156
200

46. Add the fractions:
풑 1 − 풑 풑 = .78

47. Now we plug this pooled proportion:
풑 1 − 풑 풑 = .78

48. Now we plug this pooled proportion:
풑 1 − 풑 풑 = .78
into the standard error formula in the denominator

49. Now we plug this pooled proportion:
풑 1 − 풑 풑 = .78
into the standard error formula in the denominator

50. Now we plug this pooled proportion:
.78 1−. ퟕퟖ 풑 = .78
into the standard error formula in the denominator

51. Now we plug this pooled proportion:
.78 .22
into the standard error formula in the denominator

52. Now we plug this pooled proportion:
. ퟏퟕퟐ
into the standard error formula in the denominator

53. Now we plug this pooled proportion:
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
. ퟏퟕퟐ
1
풏ퟏ
+
1
푛2
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

54. Now we need to calculate n or the sample size:
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172
1
200
+
1
푛
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

55. Now we need to calculate n or the sample size:
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172
1
200
+
1
200
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

56. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172
1
200
+
1
200
Researchers want to test the effectiveness of a new anti-anxiety
medication. In clinical testing, 64 out of 200 people
taking the medication report symptoms of anxiety. Of the
people receiving a placebo, 92 out of 200 report symptoms of
anxiety. Is the medication working any differently than the
placebo? Test this claim using alpha = 0.05.

57. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172
2
200

58. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172
1
100

59. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172 .01

60. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.172 (.1)

61. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
(.414) (.1)

62. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 =
(−. ퟏퟒ)
.0414

63. Now we need to calculate the Zstatistic
푍푠푡푎푡푖푠푡푖푐 = −3.379

64. Let’s see where this lies in the distribution:
rare
-1.96
Common rare
+1.96

65. Let’s see where this lies in the distribution:
rare
-1.96
Common rare
-3.38 +1.96

66. Because -3.38 is outside the -1.96 range we consider it
to be a rare occurrence and therefore we will reject the
null hypothesis and accept the alternative hypothesis:

67. Because -3.38 is outside the -1.96 range we consider it
to be a rare occurrence and therefore we will reject the
null hypothesis and accept the alternative hypothesis:
There was a significant difference in effectiveness between the
medication group and the placebo group, z = -3.379, p < 0.05.

68. Because -3.38 is outside the -1.96 range we consider it
to be a rare occurrence and therefore we will reject the
null hypothesis and accept the alternative hypothesis:
There was a significant difference in effectiveness between the
medication group and the placebo group, z = -3.379, p < 0.05
In summary
A two-sample Z test is used to compare the differences
statistically between two sample proportions.