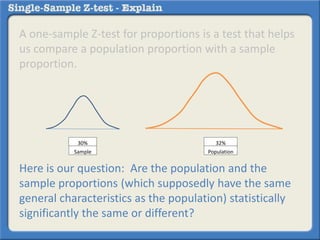
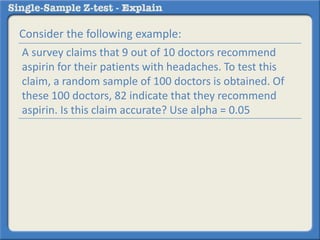
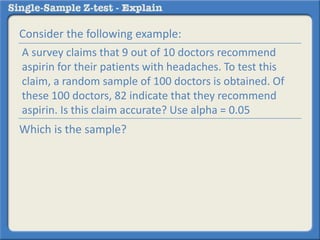
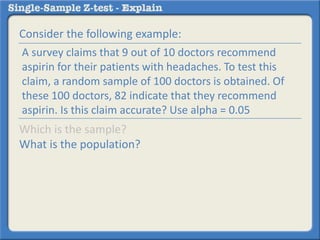
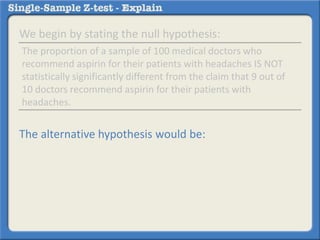
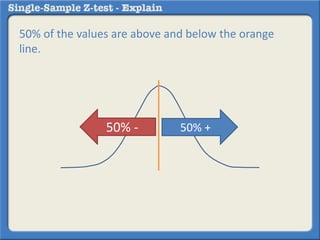
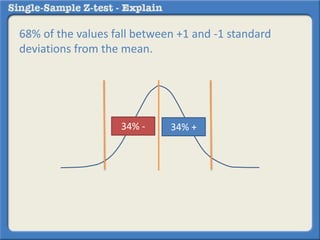
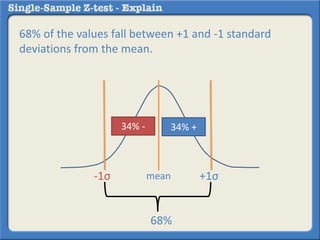
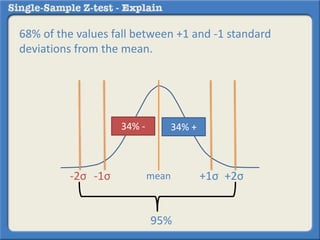
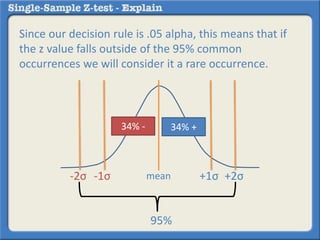
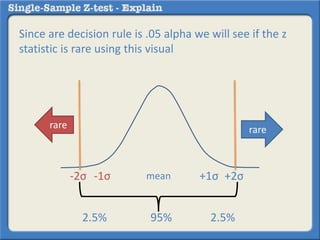
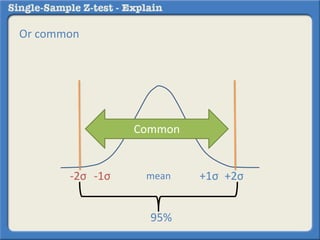
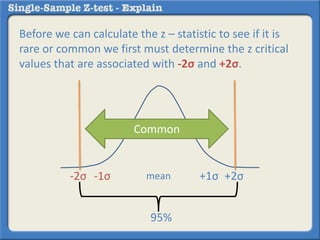
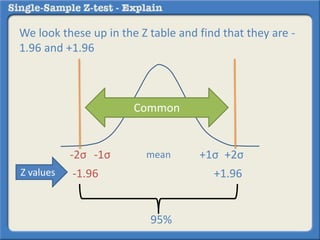
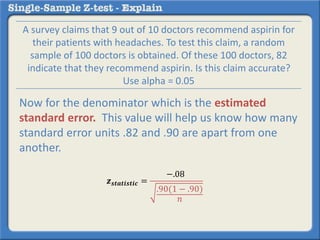
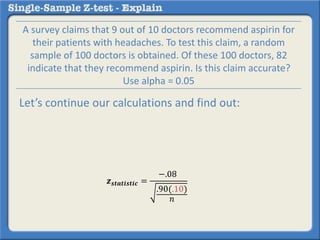
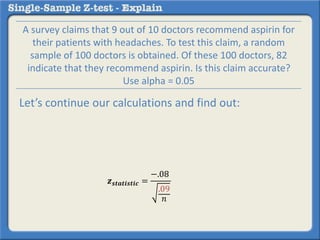
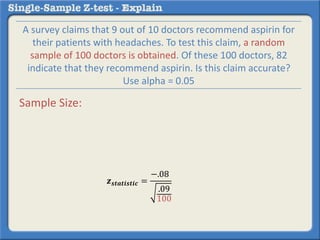
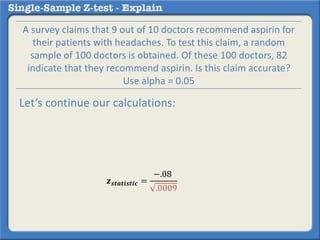
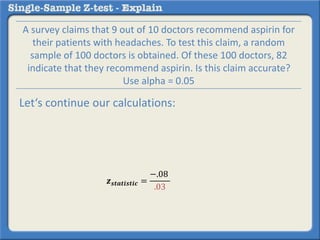
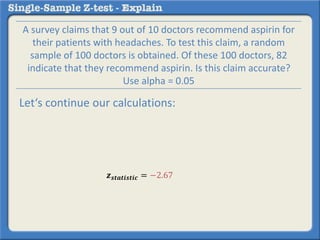
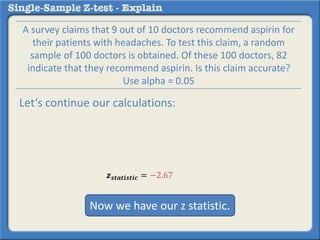
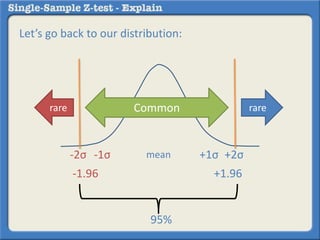
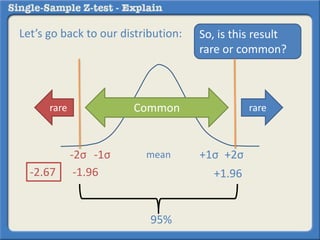
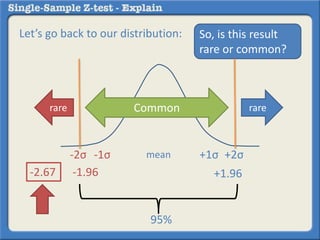
This document describes how to perform a one-sample z-test to compare a sample proportion to a population proportion. It provides an example where a survey claims 90% of doctors recommend aspirin, and a sample of 100 doctors found 82% recommend aspirin. It outlines calculating the z-statistic to determine if this difference is statistically significant using a 95% confidence level. The z-statistic is calculated to be -1.08, which falls within the acceptable range so the null hypothesis that the population and sample proportions are the same is retained.