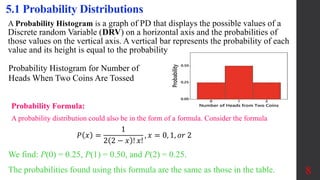
Chapter 5 covers discrete probability distributions, focusing on constructing distributions for random variables and calculating their mean, variance, and standard deviation. It explains the significance of probability distributions, including requirements and parameters, and illustrates various examples such as rolling dice and lottery probabilities. The chapter emphasizes understanding expected values and identifying significant outcomes in probability experiments.

1. Elementary Statistics
Chapter 5:
Discrete Probability
Distribution
5.1 Probability
Distribution
1

2. Chapter 5: Discrete Probability Distribution
5.1 Probability Distributions
5.2 Binomial Probability Distributions
5.3 Poisson Probability Distributions
2
Objectives:
• Construct a probability distribution for a random variable.
• Find the mean, variance, standard deviation, and expected value for a discrete
random variable.
• Find the exact probability for X successes in n trials of a binomial experiment.
• Find the mean, variance, and standard deviation for the variable of a binomial
distribution.

3. Combining Descriptive Methods and Probabilities
Construct probability distributions by presenting possible outcomes along
with the relative frequencies.
3
5.1 Probability Distributions

4. Key Concept: Random variable & Probability Distribution.
A probability histogram is a graph that visually depicts a probability distribution.
Find its important parameters such as mean, standard deviation, and variance.
Determine whether outcomes are significant (significantly low or significantly high).
Random Variable: A random variable is a variable (typically represented by x) that has a single
numerical value, determined by chance, for each outcome of a procedure.
Probability Distribution: A probability distribution is a description that gives the probability for each
value of the random variable. It is often expressed in the format of a table, formula, or graph. A
discrete probability distribution consists of the values a random variable can assume and the
corresponding probabilities of the values.
Discrete Random Variable (DRV): A discrete random variable has a collection of values that is finite
or countable. (If there are infinitely many values, the number of values is countable if it is possible to
count them individually, such as the number of tosses of a coin before getting heads.)
Continuous Random Variable: A continuous random variable has infinitely many values, and the
collection of values is not countable. (That is, it is impossible to count the individual items because at
least some of them are on a continuous scale, such as body temperatures.) 4
5.1 Probability Distributions

5. Probability Distribution Requirements (3):
1. There is a numerical (not categorical) random variable (RV)
x, and its values are associated with corresponding
probabilities.
2. ∑P(x) = 1 where x assumes all possible values. (The sum of
all probabilities must be 1, but sums such as 0.999 or 1.001
are acceptable because they result from rounding errors.)
3. 0 ≤ P(x) ≤ 1 for every individual value of the random
variable x. (That is, each probability value must be between 0
and 1 inclusive.)
5
5.1 Probability Distributions

6. Construct a probability distribution for rolling a single die.
6
Probability Distributions Outcome x P(x)
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
6 1/6
Example 2
Represent graphically the probability distribution for the
sample space for tossing 3 coins.
# of Heads: x P(x)
0 1/8
1 3/8
2 3/8
3 1/8
Example 1

7. Let’s consider tossing two coins, with the following random variable:
x = number of heads when two coins are tossed
Is this a probability distribution?
x: Number of Heads When Two
Coins Are Tossed
P(x)
0 0.25
1 0.50
2 0.25 7
Example 3 Probability Distributions
1. The variable x is a numerical random variable, and its values are associated
with probabilities.
Yes, this is.
x is a Discrete (Numerical) Random
Variable:
It has 3 possible values {0, 1, 2}
3 is a finite number.
This satisfies the requirement of being finite.
2. ∑P(x) = 0.25 + 0.50 + 0.25 = 1
3. Each value of P(x) is between 0 and 1.

8. A Probability Histogram is a graph of PD that displays the possible values of a
Discrete random Variable (DRV) on a horizontal axis and the probabilities of
those values on the vertical axis. A vertical bar represents the probability of each
value and its height is equal to the probability.
Probability Histogram for Number of
Heads When Two Coins Are Tossed
8
5.1 Probability Distributions
Probability Formula:
A probability distribution could also be in the form of a formula. Consider the formula
We find: P(0) = 0.25, P(1) = 0.50, and P(2) = 0.25.
The probabilities found using this formula are the same as those in the table.
𝑃 𝑥 =
1
2 2 − 𝑥 ! 𝑥!
, 𝑥 = 0, 1, 𝑜𝑟 2

9. Hiring managers were asked to identify the biggest mistakes that job applicants
make during an interview, and the table below is based on their responses. Does
the table below describe a probability distribution?
x P(x)
Inappropriate attire 0.50
Being late 0.44
Lack of eye contact 0.33
Checking phone or texting 0.30
Total 1.57
9
Example 4 Probability Distributions
Solution: The table violates:
1st requirement:
x is not a numerical random variable.
2nd requirement: ∑P(x) = 1
The sum of the probabilities = 1.57
The table does not describe a
probability distribution.

10. Parameters of a Probability Distribution
Remember that with a probability
distribution, we have a description of a
population instead of a sample, so the
values of the mean, standard deviation,
and variance are parameters, not
statistics.
The mean, variance, and standard
deviation of a discrete probability
distribution can be found with the
following formulas:
Mean (Expected Value), Variance &
Standard Deviation of D.R.V x:
Mean (the expected value) of
occurrence per repetition (it represents
the average value of the outcome):
10
5.1 Probability Distributions
μ = 𝐸 𝑥 = 𝑥𝑝(𝑥)
𝜇 = 𝐸(𝑥) = 𝑥𝑝(𝑥)
𝜎 = (𝑥 − 𝜇)2𝑝(𝑥) = 𝑥2𝑝(𝑥) − 𝜇2 ,
Pr 𝑜 𝑜𝑓
(𝑥 − 𝜇)2𝑝(𝑥) = (𝑥2 − 2𝜇𝑥 + 𝜇2)𝑝(𝑥)
= 𝑥2𝑝(𝑥) − 𝜇[2 𝑥𝑝(𝑥) − 𝜇 𝑝 (𝑥)]
= 𝑥2
𝑝(𝑥) − 𝜇[2𝜇 − 𝜇 • 1] = 𝑥2
𝑝(𝑥) − 𝜇2
Variance:
𝜎2
= 𝑥2
⋅ 𝑃(𝑥) − 𝜇2

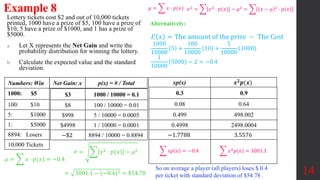
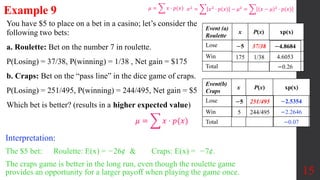
11. Example 5
Given a probability distribution for rolling a single die, find
a. the mean.
b. the variance and standard deviation.
11
Probability Distributions
𝜇 = 𝑥 ⋅ 𝑝(𝑥)
= 1 ⋅
1
6
+ 2 ⋅
1
6
+ 3 ⋅
1
6
+ 4 ⋅
1
6
+ 5 ⋅
1
6
+ 6 ⋅
1
6
=
21
6
= 3.5
Outcome x P(x)
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
6 1/6
= [12
⋅
1
6
+ 22
⋅
1
6
+ 32
⋅
1
6
+ 42
⋅
1
6
+52
⋅
1
6
+ 62
⋅
1
6
] − 3.5 2
𝜎2 = 2.91667
𝜎 = 1.70783
𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
= (𝑥 − 𝜇)2
⋅ 𝑝(𝑥)
𝜇 = 𝐸(𝑥) = 𝑥𝑝(𝑥)
𝜎 = (𝑥 − 𝜇)2𝑝(𝑥)
= 𝑥2𝑝(𝑥) − 𝜇2
𝜎2 = 𝑥2 ⋅ 𝑝(𝑥) − 𝜇2 =
Interpretation: If we were to collect data on
rolling a single die many times, we expect to
get a mean of 3.5 and SD of 1.708.

12. Example 6
The probability distribution shows the number of trips of
5 days or more that American adults take per year. Find the
mean.
12
Probability Distributions
6% take no trips of 5D+
70% take 1 trip of 5D+
20% take 2 trips of 5D+
3% take 3 trips of 5D+
1% take 4 trips of 5D+
= 0 0.06 + 1 0.70 + 2 0.20 + 3 0.03 + 4 0.01
= 1.23 𝑇𝑟𝑖𝑝𝑠
𝜇 = 𝑥 ⋅ 𝑝(𝑥)
𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
= (𝑥 − 𝜇)2
⋅ 𝑝(𝑥)
𝜇 = 𝐸(𝑥) = 𝑥𝑝(𝑥)
𝜎 = (𝑥 − 𝜇)2𝑝(𝑥)
= 𝑥2𝑝(𝑥) − 𝜇2
Interpretation: All American adults take an
average of 1.23 trips of 5 days or more per year.

13. Recall: The table describes the probability distribution for the number of heads when two coins
are tossed. A) Find the mean, variance, and standard deviation for the probability distribution
described. B) Use these results and the range rule of thumb to determine whether 2
heads is a significantly high number of heads.
13
Example 7 Probability Distributions
x: Number of Heads When
Two Coins Are Tossed
P(x)
0 0.25
1 0.50
2 0.25
Sum
𝜇 = 𝑥 ⋅ 𝑝(𝑥)
xP(x)  
2
( )
x P x

 
  
 

0(.25) (0 − 1)20.25 = 0.25
1(.5) (1 − 1)20.50 = 0
2(.25) (2 − 1)2
0.25 = 0.25
1 0.50
𝜇 = 𝑥 ⋅ 𝑝(𝑥) = 1
𝜎2 = (𝑥 − 𝜇)2 ⋅ 𝑝(𝑥) = 0.5
𝜎 = 0.5 = 0.707107
Interpretation: If we were to collect data on a
large number of trials with two coins tossed in
each trial, we expect to get a mean of 1.0 head
and the standard deviation is 0.71 head.
B) (µ ± 2σ) = 1 ± 2(0.7) = −0.4 𝑡𝑜 2.4
No, why?
𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
= (𝑥 − 𝜇)2
⋅ 𝑝(𝑥)

14. Lottery tickets cost $2 and out of 10,000 tickets
printed, 1000 have a prize of $5, 100 have a prize of
$10, 5 have a prize of $1000, and 1 has a prize of
$5000.
a. Let X represents the Net Gain and write the
probability distribution for winning the lottery.
b. Calculate the expected value and the standard
deviation.
14
Example 8
So on average a player (all players) loses $ 0.4
per ticket with standard deviation of $54.78 .
𝜎 = 𝑥2 ⋅ 𝑝(𝑥) − 𝜇2
= 3001.1 − (−0.4)2 = $54.78
𝐸 𝑥 = The amount of the prize − The Cost
1000
10000
5 +
100
10000
10 +
5
10000
1000
1
10000
5000 − 2 = −0.4
Alternatively:
𝜇 = 𝑥 ⋅ 𝑝(𝑥) = −0.4
𝜇 = 𝑥 ⋅ 𝑝(𝑥) 𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
= (𝑥 − 𝜇)2
⋅ 𝑝(𝑥)
Numbers: Win
1000: $5
100: $10
5: $1000
1: $5000
8894: Losers
10,000 Tickets
Net Gain: x p(x) = # / Total
$3 1000 / 10000 = 0.1
$8 100 / 10000 = 0.01
$998 5 / 10000 = 0.0005
$4998 1 / 10000 = 0.0001
−$2 8894 / 10000 = 0.8894
xp(x) 𝒙𝟐𝒑(𝒙)
0.3 0.9
0.08 0.64
0.499 498.002
0.4998 2498.0004
−1.7788 3.5576
𝑥𝑝 𝑥 = −0.4 𝑥2
𝑝 𝑥 = 3001.1

15. You have $5 to place on a bet in a casino; let’s consider the
following two bets:
a. Roulette: Bet on the number 7 in roulette.
P(Losing) = 37/38, P(winning) = 1/38 , Net gain = $175
b. Craps: Bet on the “pass line” in the dice game of craps.
P(Losing) = 251/495, P(winning) = 244/495, Net gain = $5
Which bet is better? (results in a higher expected value)
15
Example 9
Event (a)
Roulette
x P(x) xp(x)
Lose
Win
Total
Event(b)
Craps
x P(x) xp(x)
Lose
Win
Total
Interpretation:
The $5 bet: Roulette: E(x) = −26¢ & Craps: E(x) = −7¢.
The craps game is better in the long run, even though the roulette game
provides an opportunity for a larger payoff when playing the game once.
−4.8684
4.6053
−0.26
−2.5354
−2.2646
−0.07
−5 37/38
175 1/38
−5 251/495
5 244/495
𝜇 = 𝑥 ⋅ 𝑝(𝑥) 𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
= (𝑥 − 𝜇)2
⋅ 𝑝(𝑥)
𝜇 = 𝑥 ⋅ 𝑝(𝑥)

16. Example 10
In a casino, the house wins on one of its games with a probability 50.6%. All
bets are 1:1. Therefore, if you win, you gain the amount you bet; If you lose,
you lose the amount you bet. If you play 200 games, betting $1 each time, how
much should you expect to win or lose?
16
Find the Expected Value
= 1(0.494) + (−1)(.506)
Event x P(x)
Lose −1 50.6%
Win 1 0.494
Total
= −0.012
Expected Value for 1 game
Expected Value for 200 games
Loss of: 200(−0.012) = −2.4
𝜇 = 𝑥 ⋅ 𝑝(𝑥)
𝜇 = 𝑥 ⋅ 𝑝(𝑥)

17. Example 11 (Time)
A talk radio station has 4 telephone lines. If the host is unable to talk (i.e., during a commercial) or is
talking to a person, the other callers are placed on hold. When all lines are in use, others who are trying
to call in get a busy signal. The probability that 0, 1, 2, 3, or 4 people will get through is shown in the
distribution.
a. Find the variance and standard deviation for the distribution.
b. Should the station have considered getting more phone lines installed?
17
= 0 0.18 + 1 0.34 + 2 0.23 + 3 0.21 + 4 0.04
= 02 0.18 + 12 0.34 + 22 0.23
+32
0.21 + 42
0.04 − 1.6 2
No, 4 phone lines should be
sufficient.
The mean number of people
calling at any one time is 1.6
& SD = 1.11
Most callers would be
accommodated by 4 phone
lines because:
By Empirical Rule: µ + 2
1.6 + 2(1.1) = 1.6 + 2.2 =
3.8.
Very few callers would get a
busy signal since at least
75% of the callers would
either get through or be put
on hold. (Chebyshev’s
theorem 𝟏 − (𝟏/𝒌𝟐
)
= 1.6
𝜇 = 𝑥 ⋅ 𝑝(𝑥) 𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
= (𝑥 − 𝜇)2
⋅ 𝑝(𝑥)
𝜇 = 𝑥 ⋅ 𝑝(𝑥)
𝜎2
= 𝑥2
⋅ 𝑝(𝑥) − 𝜇2
𝜎2 = 1.23 → 𝜎 = 1.11

18. Identifying Significant Results with Probabilities:
Significantly high number of successes:
x successes among n trials is a significantly high number of successes if the probability of x or more
successes is 0.05 or less.
x is a significantly high number of successes if P(x or more) ≤ 0.05
Significantly low number of successes:
x successes among n trials is a significantly low number of successes if the probability of x or fewer
successes is 0.05 or less.
x is a significantly low number of successes if P(x or fewer) ≤ 0.05
The value 0.05 is not absolutely rigid. Other values, such as 0.01, could be used too.
The Rare Event Rule for Inferential Statistics: If, under a given
assumption, the probability of a particular outcome is very small and the outcome occurs significantly
less than or significantly greater than what we expect with that assumption, we conclude that the
assumption is probably not correct.
18
Example: Observation: A coin is tossed 100 times and we get 98 heads in a row.
Assumption: The coin is fair. (a normal assumption when an ordinary coin is tossed)
If the assumption is true, we have observed a highly unlikely event.
According to The Rare Event Rule , therefore, what we just observed is evidence against the assumption.
On this basis, we conclude the assumption is wrong (the coin is loaded.)

19. Example 12
The table shows the prizes and probability of winning (on a single $1
ticket) for a state lottery. If you buy a $1 ticket every day for a year, how
much should you expect to win or lose? Round to the nearest dollar.
19
Find the Expected Value
( )
x p x
  
 Prize ($ x)
Probability: P(x)
28,000,000
Jackpot
1 in 76,275,360
150,000 1 in 2.179,296
5000 1 in 339,002
150 1 in 9686
100 1 in 7705
5 1 in 220
2 1 in 102
1 1 in 62
 
   
 
The amount of the prize The Cost=
1 1
28,000,000 150,000
76,275,360 2,179,296
1
... 1 1 0.4624
62
E x  
 
   
Expected Value for 1 year: 365 days
Loss of: 365(−0.4624) = −168.776
≈ $ − 169
Alternatively:
𝜇 = 𝑥 ⋅ 𝑝(𝑥)