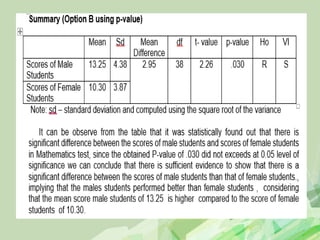
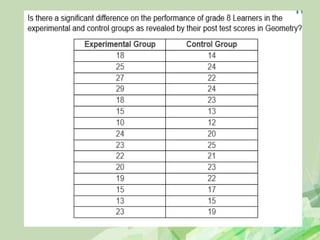
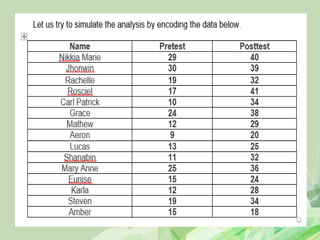
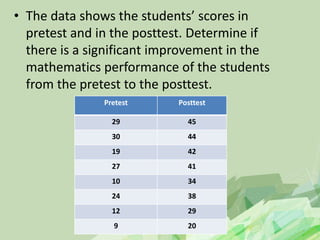
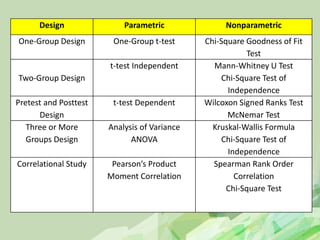
Here are the steps to solve this hypothesis testing problem: 1. State the null and alternative hypotheses: H0: There is no significant difference between the means under stress and no stress conditions. H1: There is a significant difference between the means under stress and no stress conditions. 2. Choose the level of significance: Given as α = 0.01 3. Select the appropriate statistical test: Since this involves comparing the means of two independent groups, use a two-sample t-test. 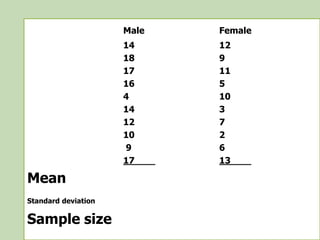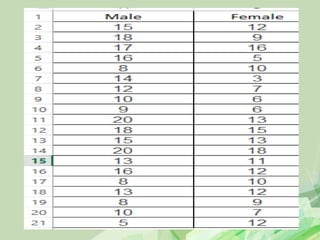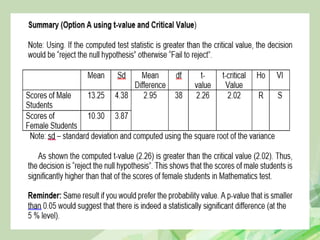4. Compute the test statistic and p-value: Follow the t-test formula and calculation. 5. Make a decision: Reject H0 if p-value < α, fail to reject H0 if

1. Hypothesis Testing
• Hypothesis testing is an area of
statistical inference in which one
evaluates a conjecture about some
characteristic of the present
population based upon the
information contained in the
random sample. Usually the
conjecture concerns one of the
unknown parameters of the
population.

2. Hypothesis Testing
• A hypothesis is a claim or
statement about the population
parameter. Usual parameters are
population mean or proportion.
In hypothesis testing, parameters
must be identified before
analysis.

3. Example of Hypothesis:
• The mean scholastic rating of
students admitted in URS is not
less than 80%.
• The proportion of registered
voters in Antipolo City favoring a
candidate A exceeds 0.60.

4. • Researchers must always keep in
mind that they analyze a sample
data in an attempt to distinguish
between results easily occur and
results that are highly unlikely.
Occurrence of highly unlikely
results can only be explained by
either that a rare event has
indeed occurred or that things
are not as they are assumed to
be.

5. To perform hypothesis testing,
the following steps are usually
followed:
Step 1:Formulate a null and
alternative hypothesis. Every
hypothesis-testing situation
begins with the statement of a
hypothesis.

6. • A statistical hypothesis is a conjecture about
a population parameter. This conjecture may
or may not be true. The null hypothesis,
symbolized by Ho, is a statistical hypothesis
that states that there is no difference
between a parameter and a specific value or
that there is no difference between two
parameters. The alternative hypothesis,
symbolized by H1, is a statistical hypothesis
that states a specific difference between a
parameter and a specific value or that there
is difference between two parameters.

7. Example: A researcher is interested in
finding out whether a new medication
will have any undesirable side effects.
The researcher is particularly
concerned with the pulse rate of the
patients who take the medication. Will
the pulse rate increase, decrease, or
remain unchanged after a patient
takes the medication? Suppose that
the mean rate for the population
under study is 82 beats per minute.

8. H0: There is no significant difference between
the pulse rate of patients exposed to a new
medication and the 82 beats per minute mean
rate for the population under study.
H1: There is a significant difference between
the pulse rate of patients exposed to a new
medication and the 82 beats per minute mean
rate for the population under study.
Critical Value: 82 beats per minute

9. • State the null and alternative for each of
the following problems
A psychologist feels that playing soft music
during a test will change results of the test.
The psychologist is not sure whether the
grades will be higher or lower. In past, the
mean of the scores was 73.
Ho:________________________________
H1: ________________________________

10. A chemist invents an additive to increase the life of an
automobile battery. If the mean lifetime of the
automobile battery is 36 months, then what would be
his hypotheses?
• H0: There is no significant difference between the
average life of an automobile battery with an
additive and the mean life of a regular battery
which is 36 months.
• H1: There is a significant difference between the
average life of an automobile battery with an
additive and the mean life of a regular battery
which is 36 months.
• Critical Value: 36 months

11. Is there a significant difference between
the performance of grade 9 learners
before and after exposure to the
developed Learning Materials in
Physics?
• Ho:____________________________
• H1:____________________________

12. • Step 2: After stating the null and alternative
hypotheses, the researcher’s next step is to design
study. The researcher selects the correct
statistical test.
• Statistics is the universal language of research. A
researcher will need to know statistics in order to
formulate statement of the problems, state
hypotheses, develop and validate instruments,
organize and analyze data, and make conclusion
on the basis of the analysis. As a researcher, we
need to master both the “science” and the “art”
of using statistical methodology correctly. Careful
use of statistical methods will enable us to obtain
accurate information from data.

13. Design Parametric Nonparametric
One-Group Design One-Group t-test Chi-Square Goodness of Fit
Test
Two-Group Design
t-test Independent Mann-Whitney U Test
Chi-Square Test of
Independence
Pretest and Posttest
Design
t-test Dependent Wilcoxon Signed Ranks Test
McNemar Test
Three or More
Groups Design
Analysis of Variance
ANOVA
Kruskal-Wallis Formula
Chi-Square Test of
Independence
Correlational Study Pearson’s Product
Moment Correlation
Spearman Rank Order
Correlation
Chi-Square Test

14. • A statistical test uses the data obtained from a
sample to make a decision about whether or
not the null hypothesis should be rejected. The
numerical value obtained from a statistical test
is called the test value.
Possible Outcomes of a Hypothesis Test
Type 1 Error occurs if one rejects the null
hypothesis when it is true.
Type 2 Error occurs if one accepts the null
hypothesis when it is false.

15. Step 3:Choose an appropriate level
of significance.
Step 4:Compute the test value.
Step 5:Make the decision to reject
or not reject the null hypothesis.
Step 6:Summarize the result.

16. The Conclusion and Interpretation of Data
• If the decision is “reject Ho”, then the
conclusion should be worded something like,
“There is sufficient evidence at the alpha level
of significance to show that…(the meaning of
alternative hypothesis).”
• If the decision is “Fail to reject Ho”, then the
conclusion should be worded something like,
There is no sufficient evidence at the alpha
level of significance to show that…(the
meaning of the alternative hypothesis.”

17. • We must always remember that
when the decision is made, nothing
has been proved. Both decisions can
lead to errors: “Fail to reject Ho”
could be type II error and “Reject
Ho” could be a type I error.

18. Probability-Value, or p-Value
• It is the probability that the test statistic could be
the value it is or a more extreme value (in the
direction of the alternative hypothesis) when the
null hypothesis is true. It is the probability of
obtaining sample mean difference as far apart as
we have, if the null hypothesis were true.
• If the p-value is less than or equal to the level of
significance alpha, then the decision must be
“Reject Ho”.
• If the p-value is greater than the level of
significance alpha, then the decision must be “Fail
to reject Ho”.

19. Test of Normality
An assumption in Parametric Test

20. According to Statistics Laerd
Your data can be checked to
determine whether it is normally
distributed using a variety of tests.
This section of the guide will
concentrate on one of the most
common methods: the Shapiro-
Wilk test of normality.

21. According to Statistics Laerd
This is a numerical method and the result of
this test is available in the output because it
was run when you selected the Normality
plots with tests option in the Explore: Plots
dialogue box. Other methods of
determining if your data is normally
distributed, such as skewness and kurtosis
values, or histograms, can be found in our
Testing for Normality guide.

22. Furthermore :
The Shapiro-Wilk test is
recommended if you have small
sample sizes (< 50 participants) and
are not confident visually
interpreting Normal Q-Q Plots or
other graphical methods.

23. Furthermore :
The Shapiro-Wilk test tests if data
is normally distributed for each
group of the independent variable.
Therefore, there will be as many
Shapiro-Wilk tests as there are
groups of the independent
variable.

25. Mean Comparison
OBJECTIVES
- to determine the appropriate
method in comparing means

27. T-test for independent samples
- it is used to test the significance of
the difference between two groups
on a certain criterion variable when
data are expressed in the interval
scale.

28. Why do we used the t-test for independent
sample?
• The t-test is used for the
independent sample because it
is more powerful test
compared with other tests of
difference of two independent
groups?

31. Example: Testing the Difference Between Two
Population Means (independent samples)
The following are the scores of 10 male
and 10 female students in spelling. Test
the null hypothesis that there is no
significant between the performance of
male and female students in the test.
α=0.05 level of significance.

32. Male Female
14 12
18 9
17 11
16 5
4 10
14 3
12 7
10 2
9 6
17 13
Mean
Standard deviation
Sample size

33. t = 131 - 7.8____________
√(4.41)2 /10 +(3.79)2 /10
= 2.88

34. The following are the scores of 20
male and 20 female students in
Mathematics test. Test the null
hypothesis that there is no significant
between the scores of male students
and scores of female students in
Mathematics test. α=0.05 level of
significance.

39. T- test for dependent samples
 It is used to determine the significance of the
difference between two dependent or correlated
samples, data are expressed in the interval scale.
Usually it is used in pre-post experimental design to
determine whether a certain treatment is effective or
not. The subjects are given a pretest, undergo the
treatment, e.g., a new method of teaching, then given
the same test as post test. In this case, there is only
one group involved. This group is administered the
same instrument twice, and the difference between
the pretest and posttest is subjected to a t-test for
dependent samples.

40. • At the start of the school year, a teacher
identified the fifteen (15) students in her class
with the lowest grade in Mathematics in the
previous year level. She wanted to give remedial
lessons to these students to improve their
performance in Mathematics. She design a
remedial mathematics program and developed a
test composed of 50 items to measure
mathematics performance. She administered the
Pre-test to the fifteen (15) students before giving
them the remedial lessons. Then, she conducted
a remedial lessons. After three weeks, she again
administered the post-test to the same students.

44. Example: At the start of the school year, a teacher
identified the eight students in her class with the
lowest grade in Mathematics in the previous year
level. She wanted to give remedial lessons to these
students to improved their performance in
Mathematics. She design a remedial mathematics
program and developed an achievement test
composed of 50 items to measure mathematics
performance. She administer ed the achievement
test to the 8 students before giving them the
remedial lessons. Then, she conducted a remedial
lessons. After three weeks, she again administered
the same achievement test.

45. • The data shows the students’ scores in
pretest and in the posttest. Determine if
there is a significant improvement in the
mathematics performance of the students
from the pretest to the posttest.
Pretest Posttest
29 45
30 44
19 42
27 41
10 34
24 38
12 29
9 20

46. t-test for Dependent Sample

47. Workshop # 2
1. English test was administered to 19 boys and 21
girls, Test whether the girls differ in their scores
from that of the boys. Use α=0.05. Follow the steps
in hypothesis testing.
Boys: 30, 28, 25, 24, 16, 10, 19, 27, 28,16,
15, 23, 20, 18, 17, 12, 28, 9, 15.
Girls: 27,18, 15, 10, 25, 29, 19, 23, 26, 20,
18, 10, 16, 28, 29, 24, 20, 24, 27, 12, 9.

48. 2. Is there a significant improvement in the
learning process of the students based from
their pre-evaluation and post evaluation
conducted by their teacher?
Data:
Student No. 1 2 3 4 5 6 7 8 9 10
Pre-Evaluation 25 23 30 7 3 22 12 30 5 14
Post-Evaluation 28 19 34 10 6 26 13 47 16 9

49. 3. The data below are those obtained for a group of 10
subjects on a choice- reaction time experiment
under stress and no stress condition. The problem
here is to test whether the means under the two
conditions are significantly different.α= 0.01
Subject: 1 2 3 4 5 6 7 8 9 10
Stress: 9 10 4 15 6 5 9 10 6 12
No stress: 5 15 7 8 4 9 8 15 6 16