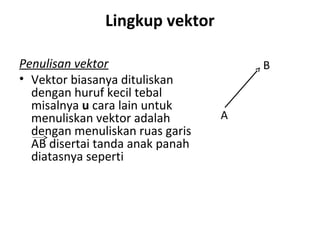
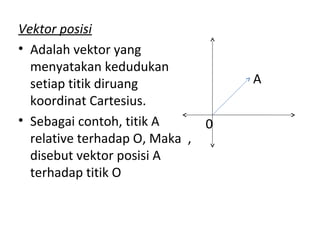
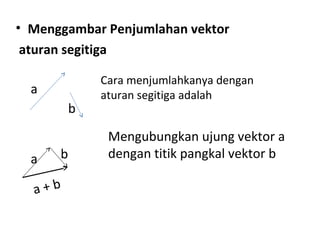
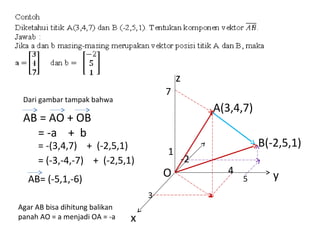
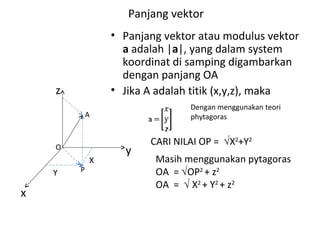
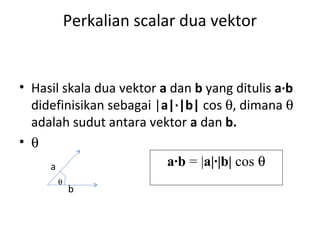
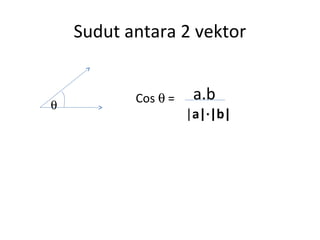
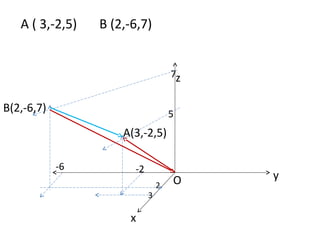
Vektor adalah besaran yang memiliki besar dan arah. Vektor dapat ditulis dengan huruf kecil tebal atau garis panjang dengan anak panah diatasnya. Modulus vektor adalah panjang vektor. Vektor dapat dioperasikan dengan penjumlahan, pengurangan, perkalian skalar, dan dihitung sudut antar vektor menggunakan kosinus.

1. VEKTOR
VECTOR

2. Pengertian Vektor
• vektor adalah suatu besaran yang
mempunyai besar dan arah.
• Misalnya : kecepatan, percepatan, dan lain-
lain.

3. Lingkup vektor
Penulisan vektor
• Vektor biasanya dituliskan
dengan huruf kecil tebal
misalnya u cara lain untuk
menuliskan vektor adalah
dengan menuliskan ruas garis
AB disertai tanda anak panah
diatasnya seperti
A
B

4. Modulus Vektor
• Modulus vektor adalah ukuran (panjang)
vektor u dan ditulis dengan notasi |u|,
dimana
• |u| = √x2
+y2
x
y

5. Vektor posisi
• Adalah vektor yang
menyatakan kedudukan
setiap titik diruang
koordinat Cartesius.
• Sebagai contoh, titik A
relative terhadap O, Maka ,
disebut vektor posisi A
terhadap titik O
0
A

6. Kesamaan dua vektor
• Dua vektor dikatakan
sama apabila panjang
serta arahnya sama
• a=b, jika |a| = |b| atau
arah a = arah b
a b

7. • Vektor –a mempunyai
ukuran yang sama
dengan vektor a tetapi
arahnya berlawanan. Jika
vektor –a = b. Maka |a| =
|-b|, vektor negative
sering disebut sebagai
vektor invers
a b

8. OPERASI PADA VEKTOR
Perkalian vektor dengan skalar
• Jika k bilangan real yang
positif, maka ku adalah vektor
yang panjangnya k |u| dan
mempunyai arah yang sama
dengan u. Sedangkan – ku
adalah vektor yang
panjangnya k |u| tetapi
berlawanan arah dengan u.
u
2u

9. • Menggambar Penjumlahan vektor
aturan segitiga
Cara menjumlahkanya dengan
aturan segitiga adalah
Mengubungkan ujung vektor a
dengan titik pangkal vektor b
a
b
a b
a + b

10. Cara jajaran genjang
• AB dan DC mewakili vektor a,
• dan AD dan BC mewakili vektor b.
• Maka AC = a+b. Cara kedua ini
disebut penjumlahan vektor dengan
aturan jajaran genjang
a+b
b
aA
B
C
D a
b

11. Contoh Penjumlahan
a + b =
a
b

12. PENJUMLAHAN 3 VEKTOR
• Untuk menjumlahkan tiga buah
vektor a,b dan c dapat kita lakukan
terlebih dahulu menjumlahkan
vektor a dan b. Setelah resultan
kedua vektor itu dicari kemudian
jumlahkan vektor C
a
b c
a+b+c
a+b
b
ac

13. Pengurangan atau selisih
• Selisih dua vektor a dan b
dinyatakan sebagai a – b,
dapat dipandang sebagai
penjumlahan vektor a
dan dengan invers vektor
b, yaitu vektor -b
a - b
ab
- b
a
- b

14. Konsep Vektor pada bangun ruang (Dimensi
Tiga)
• Koordinat ruang
dimensi tiga terdiri
atas sumbu OX,OY,
dan OZ yang satu sama
lain saling tegak lurus.
Sebuah titik dalam
ruang dimensi tiga
disajikan dalam
pasangan berurutan
(x,y,z)
Koordinat bangun ruang
x
y
z

15. cara menggambar vektor pada bangun ruang
(Dimensi Tiga)
• Gambarlah vektor r
dengan titik (3,4,6)
x
y
z
3
4
6

16. Mencari komponen
vektor pada bangun
ruang

17. x
y
z
4
7
-2
5
3
O
A(3,4,7)
B(-2,5,1)
Dari gambar tampak bahwa
AB = AO + OB
= -a + b
= -(3,4,7) + (-2,5,1)
= (-3,-4,-7) + (-2,5,1)
AB= (-5,1,-6)
1
Agar AB bisa dihitung balikan
panah AO = a menjadi OA = -a

18. Panjang vektor
• Panjang vektor atau modulus vektor
a adalah |a|, yang dalam system
koordinat di samping digambarkan
dengan panjang OA
• Jika A adalah titik (x,y,z), maka
x
y
z
Dengan menggunakan teori
phytagoras
Y
X
O
P
CARI NILAI OP = √X2
+Y2
Masih menggunakan pytagoras
OA = √OP2
+ z2
OA = √ X2
+ Y2
+ z2
A

19. Operasi pada vektor

20. Contoh :
Diketahui titik A(5,4,6) dan B(-2,5,1). Tentukan jarak antara titik A dan B
d=√(-2-5)2
+ (5-4)2
+ (1-6)2
d=√49+1+25
d=√75 = 5 √3

21. Perkalian scalar dua vektor
• Hasil skala dua vektor a dan b yang ditulis a∙b
didefinisikan sebagai |a|∙|b| cos θ, dimana θ
adalah sudut antara vektor a dan b.
• θ
θ
a∙b = |a|∙|b| cos θa
b

22. contoh
• Tentukan hasil scalar vektor a dan b pada, jika
|a|= 5, |b|=6 dan besar sudut antara vektor a
dan b adalah 600
• Jawab : a∙b = 5 x 6 x cos 600
• = 30 x 0,5
• = 15

23. Sifat-sifat Hasil kali scalar
• Dua vektor yang saling sejajar
Jika a dan b merupakan dua vektor yang arahnya sama,
maka
a∙b = |a|∙|b| cos 0o
= |a|∙|b| ∙ 1
= |a|∙|b|0 ba

24. Dua vektor yang saling tegak lurus
a∙b = |a|∙|b| cos 90o
= |a|∙|b| ∙ 0
= 0
a
b
0

25. Dua vektor yang saling berlawanan
arah
• a∙b = |a|∙|b| cos 180o
= |a|∙|b| ∙ (-1)
= - |a|∙|b|
0a b

26. Perkalian scalar dua vektor dalam bentuk komponen
misalkan vektor a dan b dinyatakan dengan bentuk
tripel berikut ini,
a= a1i + a2j+ a3k dan b = b1i + b2j+ b3k
maka
a∙b = (a1i + a2j+ a3k) ∙ (b1i + b2j+ b3k)
• Dengan menggunakan sifat distributive dan hasil kali 2 vektor basis
yang saling tegak lurus dan searah berikut,
• i∙i = 1, j∙j = 1, k∙k = 1, i∙j = 0, i∙k = 0, j∙k = 0
• maka perkalian scalar di atas dapat disajikan pada table berikut .
a.b b1i b2j b3k
a1i a1b1 0 0
a1j 0 a1b1 0
a1k 0 0 a1b1

27. • Dengan demikian, kita peroleh rumus hasil kali scalar
2 vektor sebagai berikut
a∙b = a1b1 + a2b2 + a3b3
Contoh :
Diberikan vektor –vektor sebagai berikut :
a = (1,2,4) b = (5,2,0)
Tentukan hasil kali scalar dua vektor tersebut
Jawab :
a∙b = 1.5 + 2.4 + 4.0
= 5 + 8 + 0
a∙b = 13

28. Sudut antara 2 vektor
Cos θ = a.b
|a|∙|b|
θ

29. x
y
z
-6
7
-2
2
3
O
A(3,-2,5)
B(2,-6,7) 5
A ( 3,-2,5) B (2,-6,7)