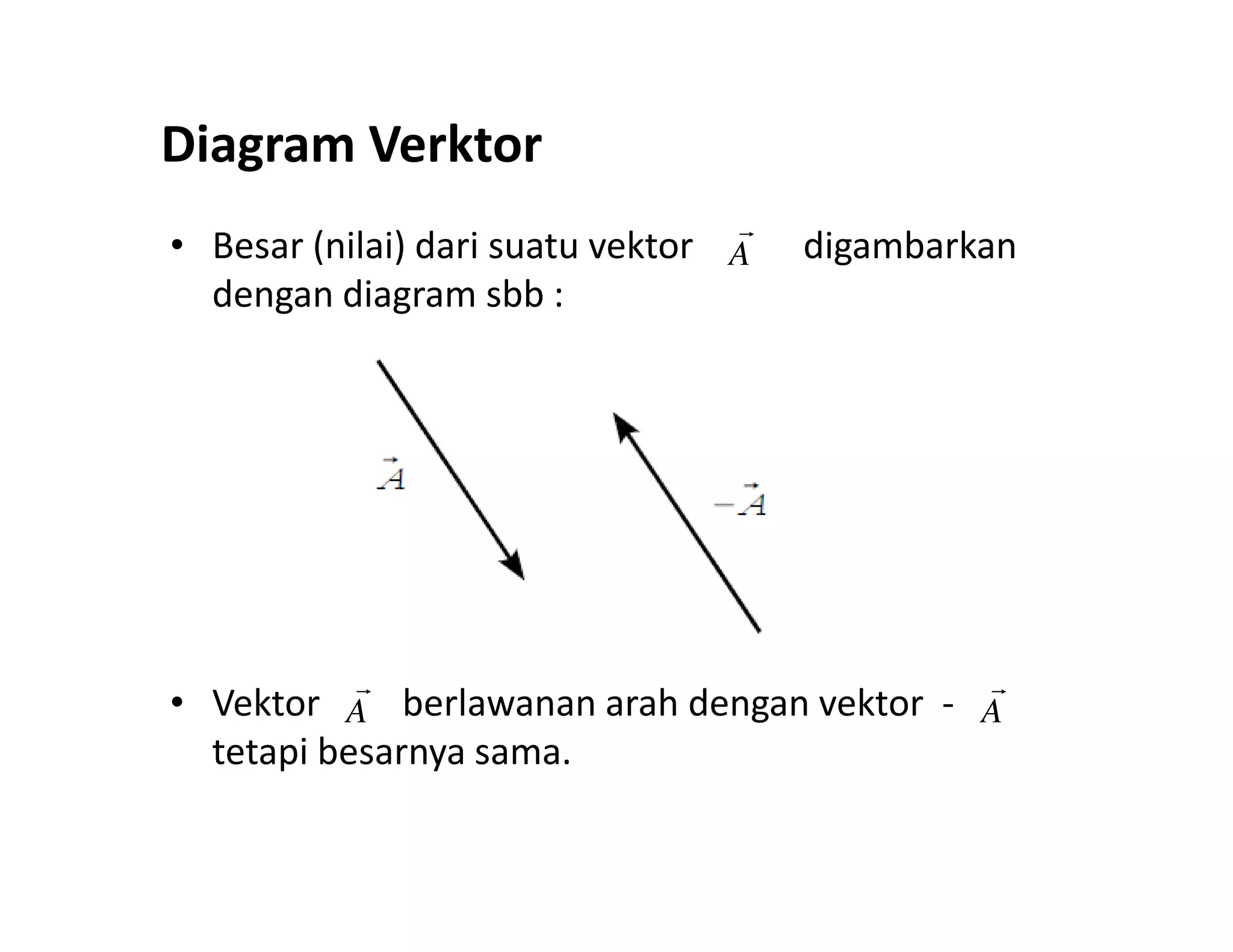
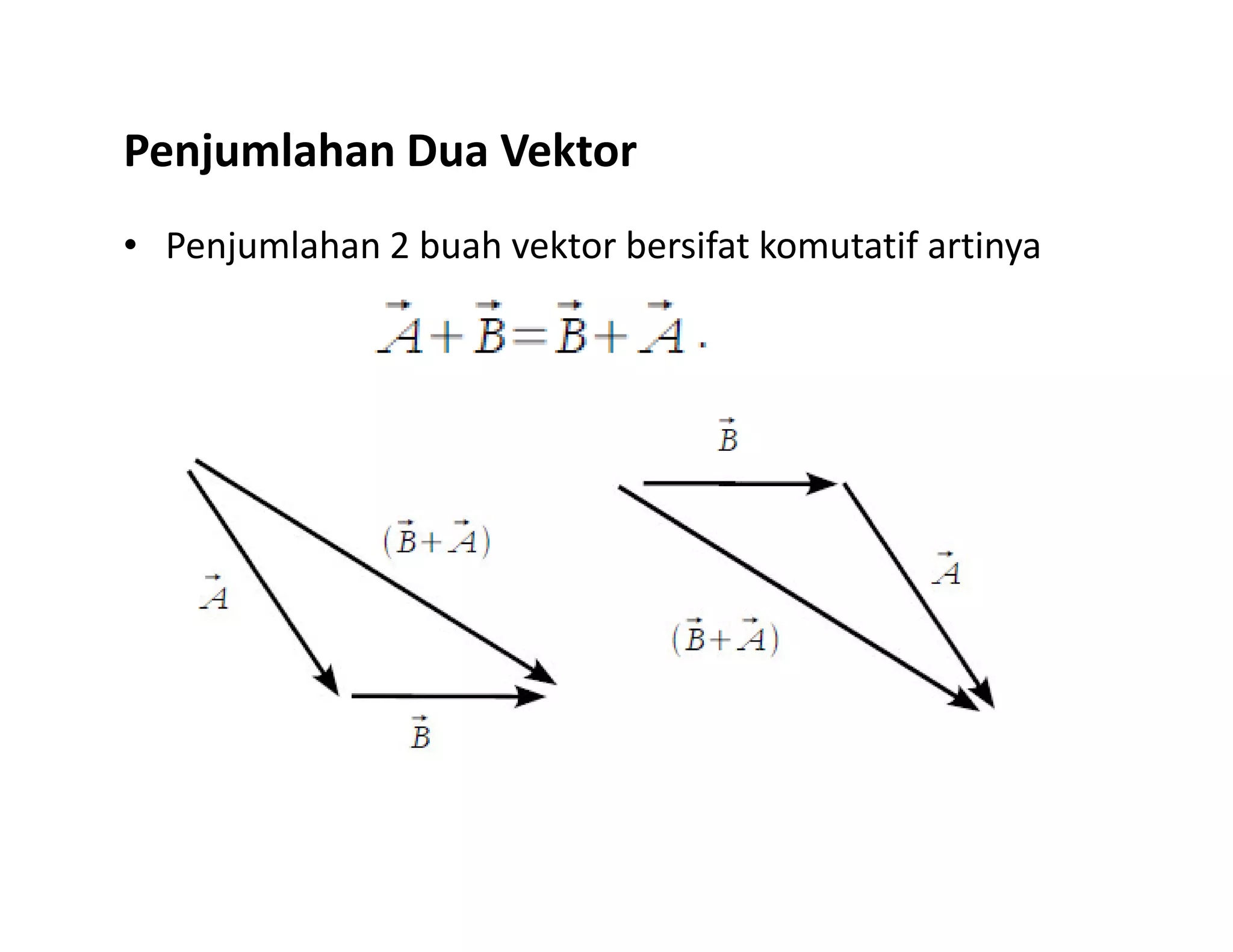
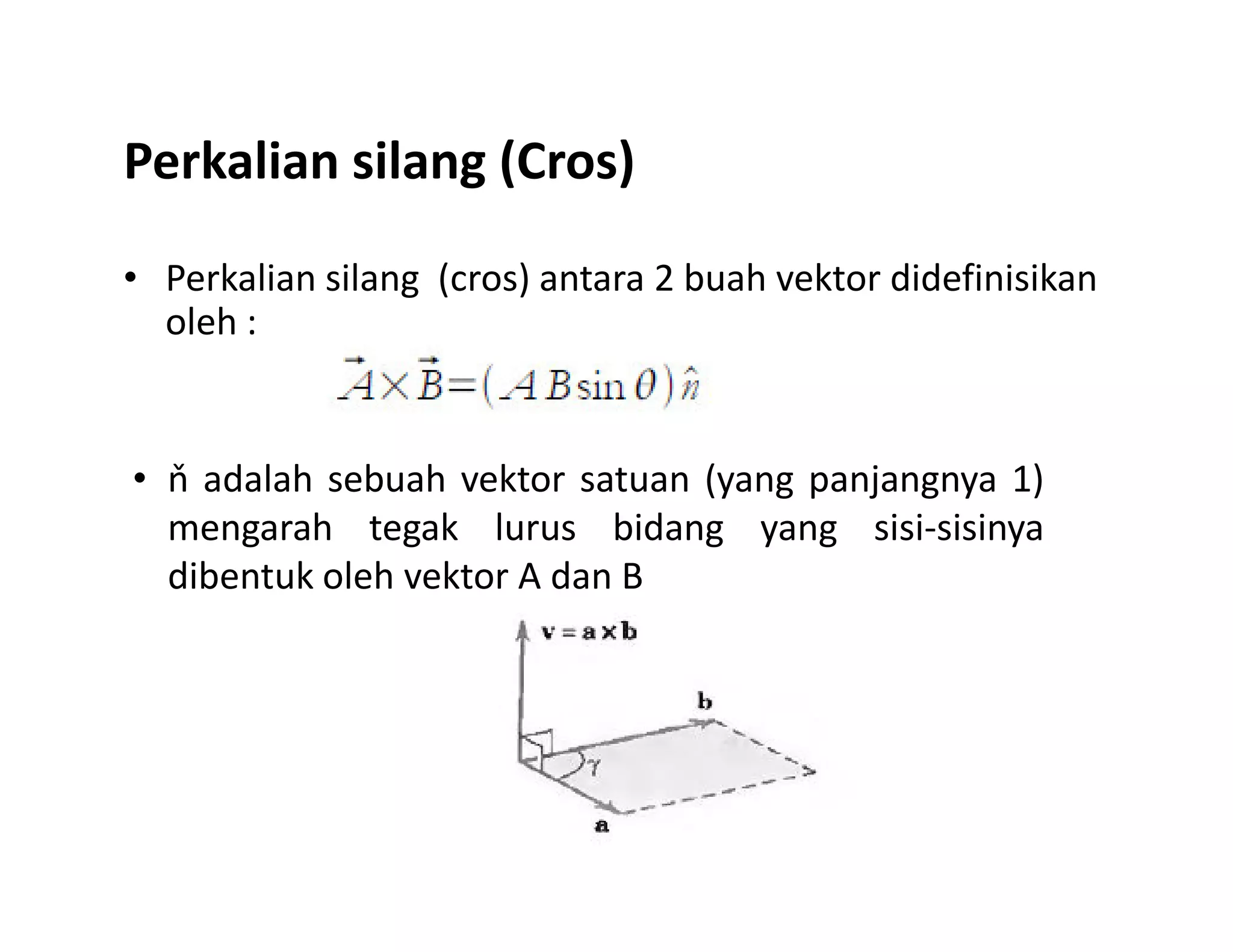
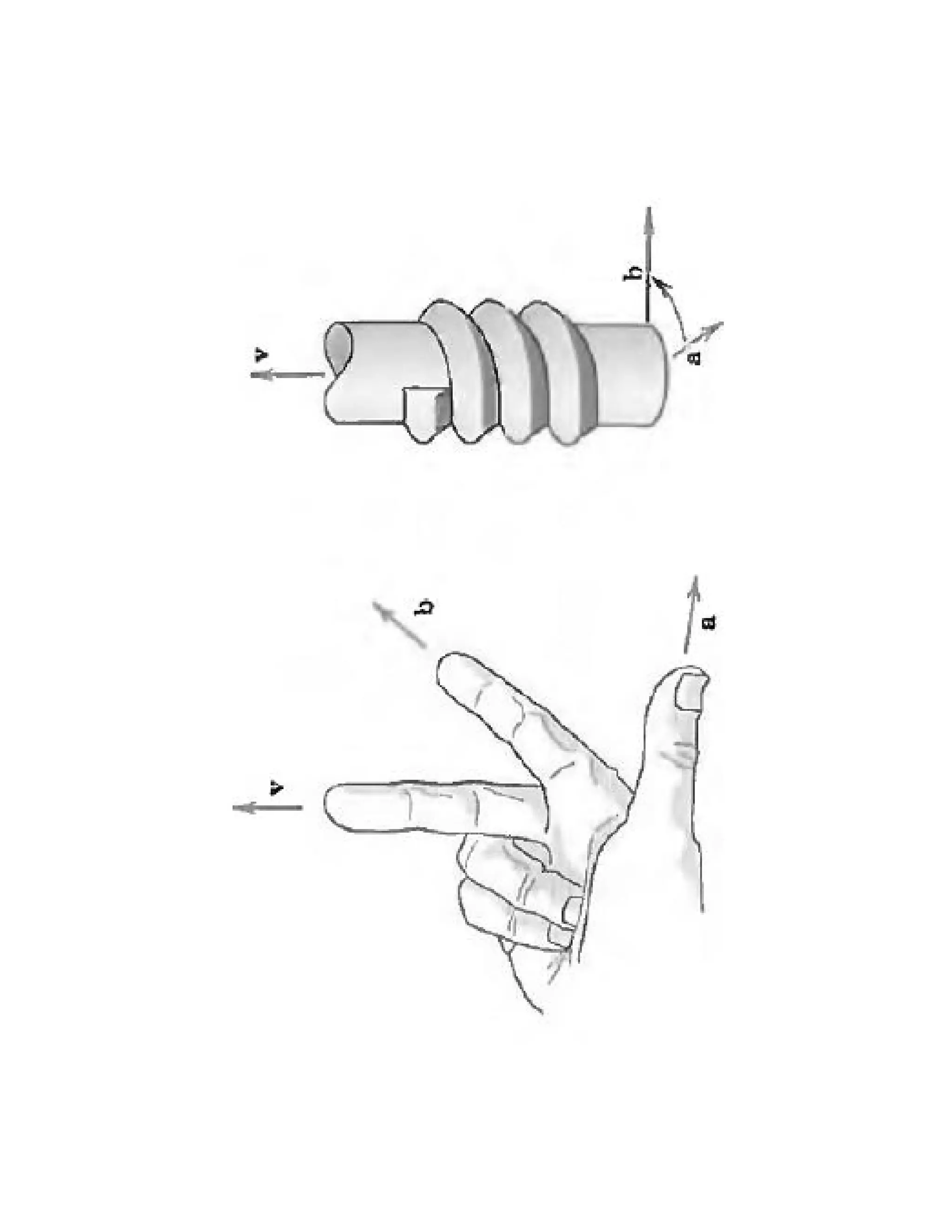
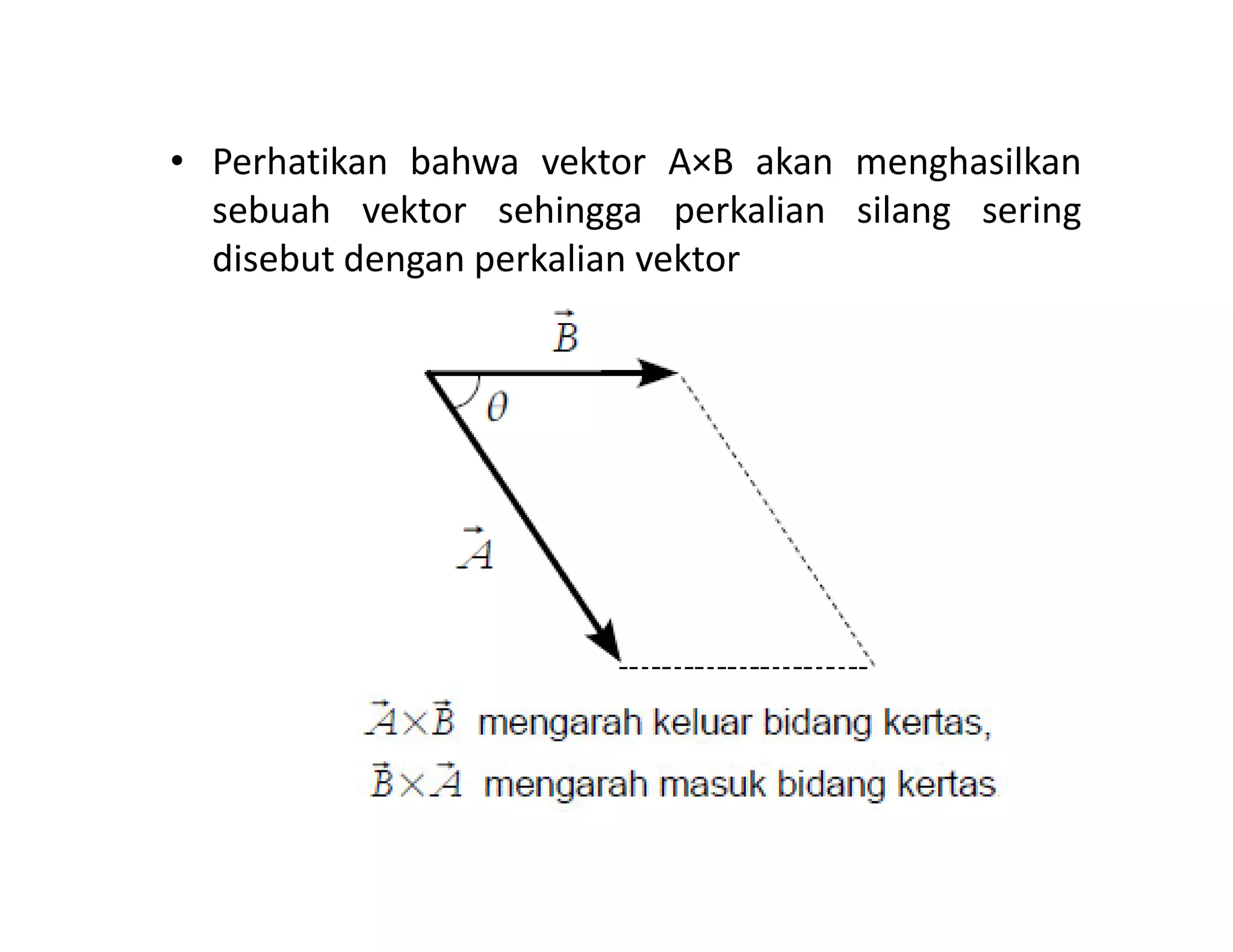
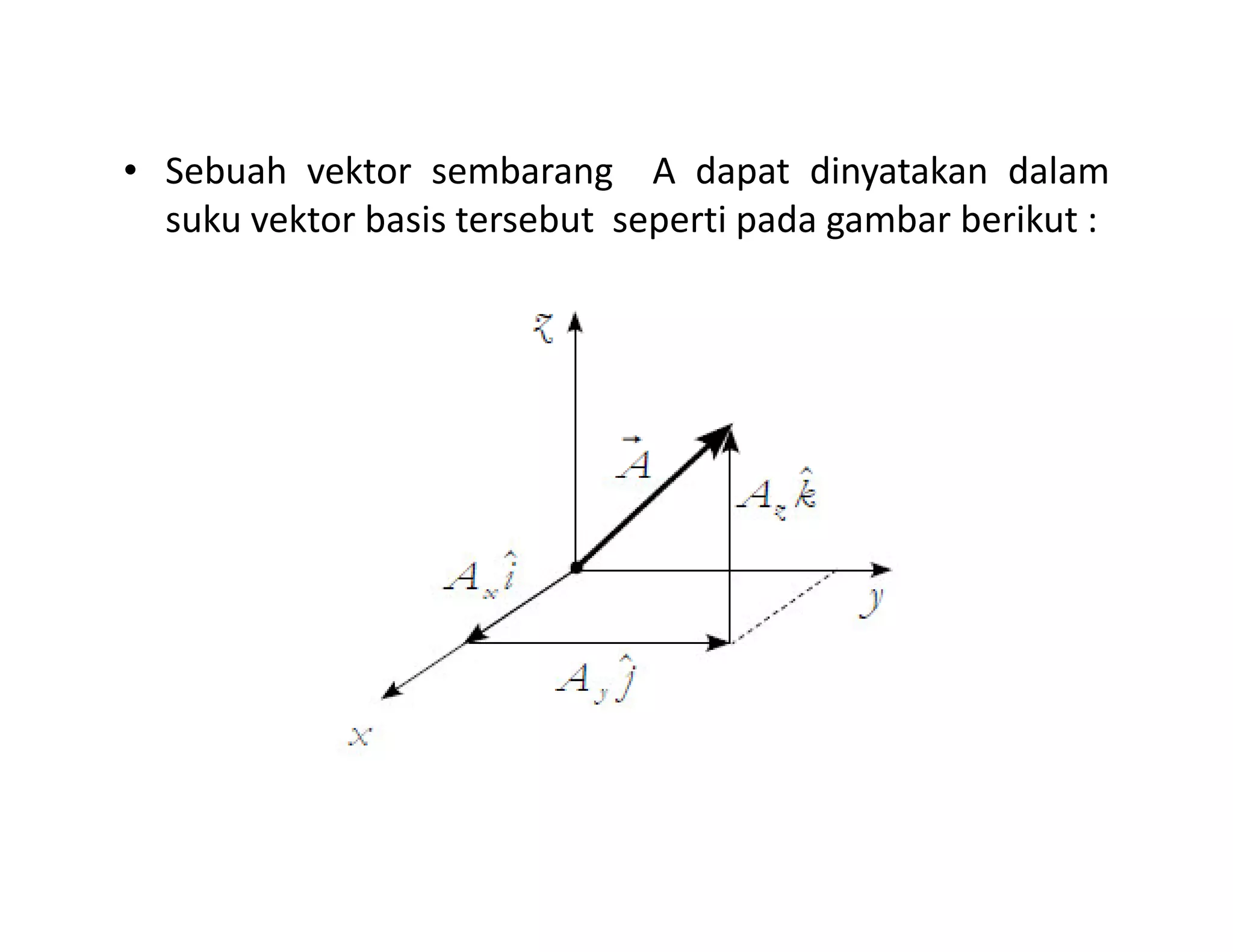
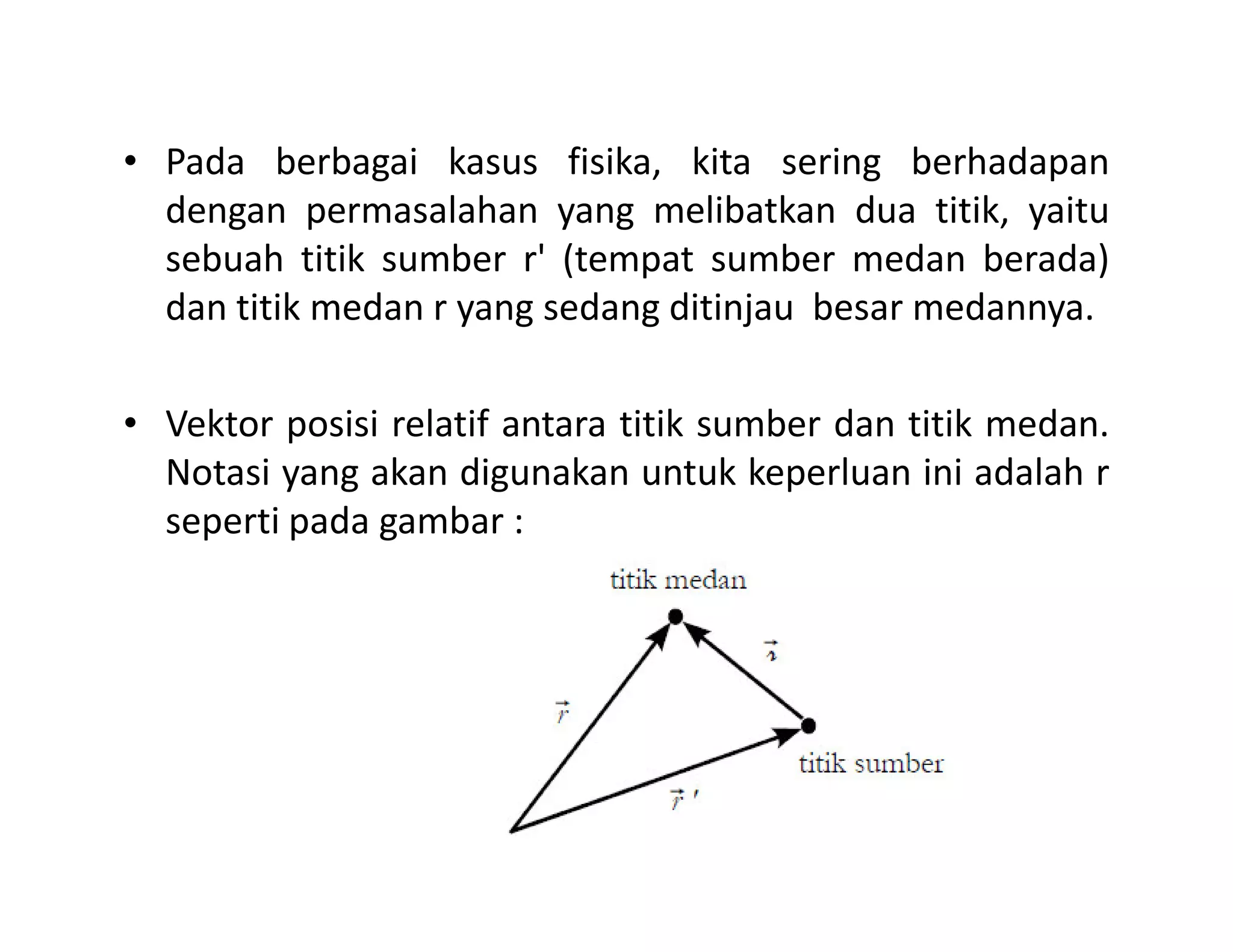
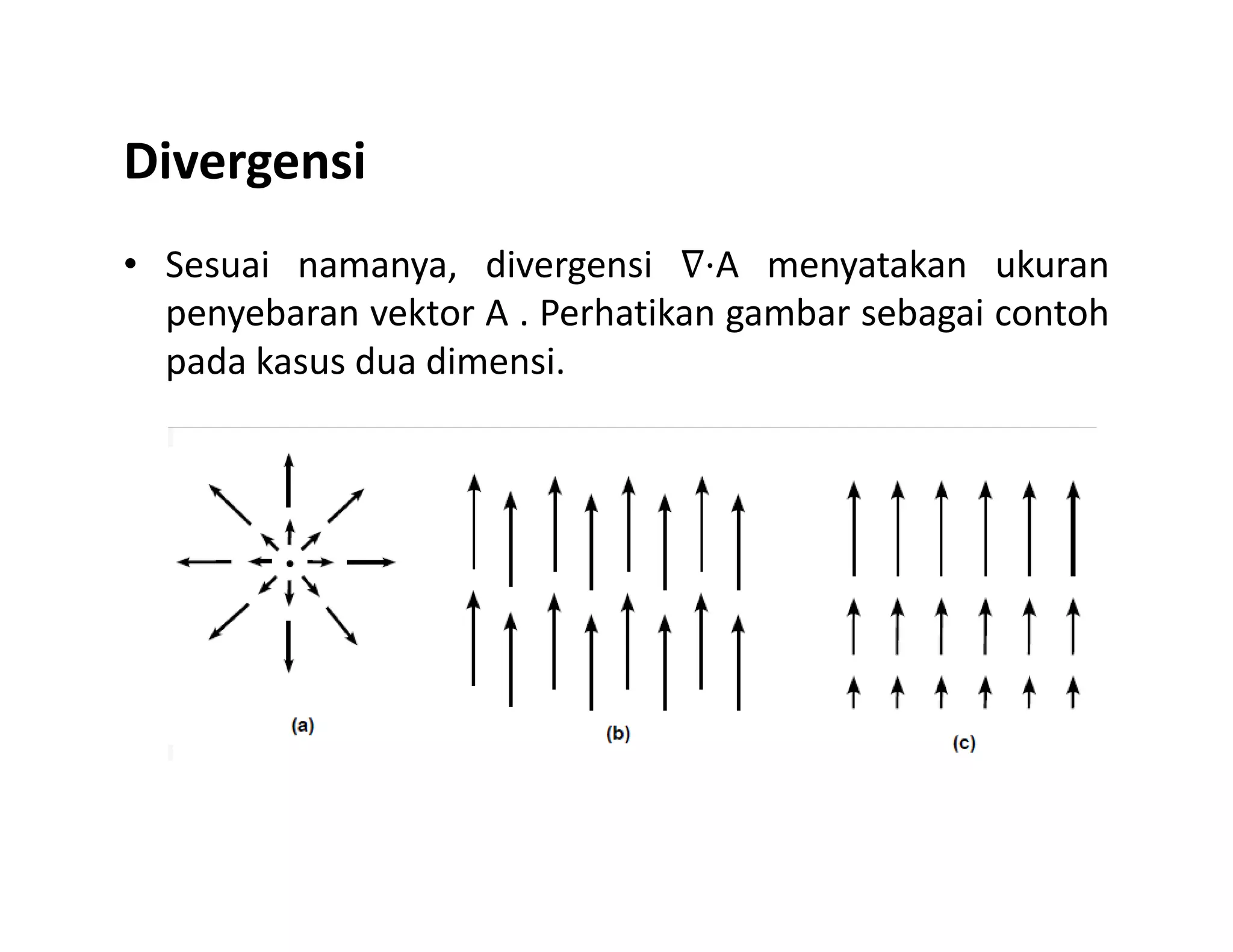
Dokumen ini membahas konsep dasar vektor dan skalar dalam fisika, termasuk definisi, notasi, serta operasi-operasi dasar seperti penjumlahan, perkalian skalar, dan perkalian silang. Selain itu, dibahas juga komponen vektor dalam sistem koordinat dan aplikasi dalam medan vektor serta konsep gradien, divergensi, dan curl. Contoh soal diberikan untuk menerapkan konsep-konsep yang dibahas.

1. ANALISIS VEKTOR
Simon Patabang, ST., MT.
Fakultas Teknik
Jurusan Teknik Elektro
Universitas Atma Jaya Makasar

2. Vektor dan Skalar
• Vektor adalah besaran yang memiliki nilai dan arah.
• Contohnya : perpindahan, kecepatan, percepatan,
gaya, dan momentum.
Skalar adalah besaran yang hanya memiliki nilai tanpa• Skalar adalah besaran yang hanya memiliki nilai tanpa
arah.
• Contohnya : massa, muatan, kerapatan, dan
temperatur

3. Notasi
• Vektor dilambangkan dengan tanda panah di atas
simbolnya.
• Misalnya Vektor A dilambangkan dengan notasi
A
• Skalar dinyatakan dengan huruf biasa.
• Misalnya Skalar B dilambangkan dengan notasi B

4. • Besar (nilai) dari suatu vektor digambarkan
dengan diagram sbb :
A
Diagram Verktor
• Vektor berlawanan arah dengan vektor -
tetapi besarnya sama.
A A

5. Penjumlahan Dua Vektor
• Penjumlahan 2 buah vektor bersifat komutatif artinya

6. • Penjumlahan bersifat asosiatif:
• Untuk mengurangkan sebuah vektor , tambahkan
dengan kebalikannya seperti gambar berikut :

7. Penjumlahan 2 buah vektor a dan b sbb :
Sifat Dasar Penjumlahan sbb :
a + b = b + a
a + ( b + c ) = (a + b) + c
a + 0 = 0 + a
a + (-a) = 0

8. Perkalian Vektor dengan sebuah skalar
• Perkalian suatu vektor dengan sebuah skalar k positif
menghasilkan sebuah dengan arah yang tidak berubah
dan besarnya bertambah sebesar k kali.
• Sifat Dasar Perkalian Skalar :
1. c (a + b) = ca + cb
2. (c + k) a = ca + ka
3. c(ka) = (ck)a
4. 1a = a

9. • Jika k negatif, arah vektor berubah menjadi sebaliknya.

10. Perkalian titik (dot)
• Perkalian titik (dot) antara 2 buah vektor didefinisikan oleh
• θ adalah sudut antara vektor A dan B. Ketika kedua
ujung vektor saling bertemu maka akan menghasilkanujung vektor saling bertemu maka akan menghasilkan
sebuah skalar sehingga perkalian titik ini sering juga
disebut perkalian skalar.

11. • Perkalian bersifat komutatif
• Jika dua vektor sejajar, maka :

12. Perkalian silang (Cros)
• Perkalian silang (cros) antara 2 buah vektor didefinisikan
oleh :
• ň adalah sebuah vektor satuan (yang panjangnya 1)• ň adalah sebuah vektor satuan (yang panjangnya 1)
mengarah tegak lurus bidang yang sisi-sisinya
dibentuk oleh vektor A dan B

13. • Ada dua arah yang tegak lurus bidang tersebut,
yaitu “masuk” dan “keluar”.
• Untuk mengatasi masalah ini, digunakanlah
kesepakatan aturan tangan kanan dengan cara :
• Kepalkan keempat jari selain ibu jari agar menunjuk• Kepalkan keempat jari selain ibu jari agar menunjuk
pada vektor pertama (dengan ibu jari tegak lurus
keempat jari), kemudian putar keempatnya (pada
sudut terkecil) ke arah vektor kedua, maka ibu jari
menandakan arah dari perkalian silang kedua vektor
tersebut. Perhatikan paga gambar berikut :

15. • Perhatikan bahwa vektor A×B akan menghasilkan
sebuah vektor sehingga perkalian silang sering
disebut dengan perkalian vektor

16. • Perkalian silang bersifat distributif
• Secara geometri, ∣ Ā × B ∣ adalah luas daerah jajaran
genjang yang dibentuk oleh A dan B. Jika kedua
vektor saling sejajar, maka perkalian silangnya nol
∣ ∣
vektor saling sejajar, maka perkalian silangnya nol
dan secara khusus Ā × Ā = 0 untuk sembarang vektor
Ā .

17. Komponen Vektor
• Dalam praktik biasanya cukup mudah untuk bekerja
dengan komponen vektor dalam sistem koordinat
tertentu.
• Misalkan pada koordinat kartesian: i , j , dan k masing-
masing adalah vektor satuan yang sejajar dengan
sumbu- x, y, dan z.sumbu- x, y, dan z.

18. • Sebuah vektor sembarang A dapat dinyatakan dalam
suku vektor basis tersebut seperti pada gambar berikut :

19. • Bilangan Ax , Ay , dan Az disebut komponen dari Ā .
• Tafsiran geometri dari komponen vektor tersebut adalah
proyeksi Ā sepanjang tiga sumbu koordinat.
Dengan hasil ini, keempat operasi vektor yang telah• Dengan hasil ini, keempat operasi vektor yang telah
dijelaskan sebelumnya dapat dirumuskan ulang dalam
bentuk komponen-komponennya:

20. 1. Penjumlahan dua vektor:
2. Perkalian skalar:
3. Perkalian dot (titik)

21. 4. Perkalian silang (cros) dua vektor

23. Contoh soal dan penyelesaian
Sebuah vektor A = (2ax – 3ay + az ) dan
vektor B = ( - 4ax – 2ay + 5az).
Tentukan perkalian silang A x B ?
Penyelesaian :

24. TUGAS 2
1. Gambarlah vector-vektor berikut ini pada koordinat
kartesius 3 dimensi yang mempunyai besar dan arah
sebagai berikut :
a.Vektor A = 2ax – 3ay + 4az
b.Vektor M = -ax + 2ay + 2az
c. Vektor R = ax + 3ay - 2azc. Vektor R = ax + 3ay - 2az
d. Vektor H = -2ax - ay - 3az
2. Mengacu pada soal No. 1 Hitunglah operasi vektor
berikut ini
a. A + M – H
b. A x M
c. R . H
d. A x (M.H)

25. Vektor Posisi
• Lokasi sebuah titik dalam tiga dimensi dapat dinyatakan
dalam koordinat kartesian x , y , z .
• Vektor yang mengarah ke titik tersebut dari titik asal
disebut dengan vektor posisi:
• Besarnya
adalah jarak dari titik asal, dan

26. • ř merupakan vektor satuan yang mengarah radial keluar.
Vektor Perpindahan
Bagian kecil vektor perpindahan (jarak r) dari (x , y , z)
hingga (x + dx , y + dy , z + dz) adalah dr didefinisikanhingga (x + dx , y + dy , z + dz) adalah dr didefinisikan
sbb:

27. • Pada berbagai kasus fisika, kita sering berhadapan
dengan permasalahan yang melibatkan dua titik, yaitu
sebuah titik sumber r' (tempat sumber medan berada)
dan titik medan r yang sedang ditinjau besar medannya.
• Vektor posisi relatif antara titik sumber dan titik medan.
Notasi yang akan digunakan untuk keperluan ini adalah rNotasi yang akan digunakan untuk keperluan ini adalah r
seperti pada gambar :

28. Besar dari vektor posisi relatif tersebut adalah
'r r r= −
dan vektor satuannya (mengarah dari r ' ke r ):
'r r r−ɵ '
'
r r r
r
r r r
−
= =
−
ɵ

29. Medan Vektor
• Jika untuk setiap nilai suatu skalar u kita kaitkan sebuah
vektor Ā , maka Ā disebut fungsi dari u dan dinyatakan
dengan Ā (u).
• Notasi ini dalam tiga dimensi dapat dituliskan menjadi :
• Jika setiap titik (x , y , z ) berkaitan dengan sebuah
vektor Ā, maka Ā adalah fungsi dari (x , y , z ) yang
dinyatakan dengan :

30. • Bentuk ini menyatakan vektor Ā ini mendefinisikan
sebuah medan vektor :
• Mendefinisikan medan skalar.
( , , )x y zφ

31. • Jika :
• Maka diferensial total dari Ā(u) didefinisikan :
Turunan dari A(u) didefinisikan
• Maka diferensial total dari Ā(u) didefinisikan :

32. • Jika :
• Turunan dari perkalian vektor dengan skalar atau• Turunan dari perkalian vektor dengan skalar atau
vektor dengan vektor mengikuti aturan yang sama
seperti pada fungsi skalar.
• Ketika kita melibatkan perkalian silang maka
urutan penulisan penting untuk diperhatikan
karena terkait dengan arah dari hasil perkalian
tersebut

33. Contoh :

34. Gradien
• Misalkan sebuah operator vektor ∇ dalam koordinat
kartesian didefinisikan
• Jika dan memiliki turunan
parsial pertama yang kontinu pada daerah tertentu,
maka dapat didefinisikan beberapa besaran berikut:

35. • Gradien memiliki besar dan arah. Untuk menentukan arti
geometrinya, kita dapat memisalkan ada sebuah fungsi
tiga variabel, katakanlah temperatur dalam ruang, T (x , y
, z ) , yang merupakan sebuah skalar.
• Seberapa cepat perubahan temperatur tersebut
dinyatakan dalam bentuk diferensial totaldinyatakan dalam bentuk diferensial total

36. • Dalam bentuk perkalian titik, pernyataan di atas setara
dengan
atau
yang berarti

37. dengan θ adalah sudut antara ∇ T dan d r , kemudian u
adalah suatu vektor satuan yang menyatakan arah gerak
kita. Dengan demikian, laju perubahan temperatur ( dT /dr )
akan bernilai paling besar ketika geraknya searah dengan ∇
T (yaitu saat θ =0 ).

38. Divergensi
• Sesuai namanya, divergensi ∇⋅A menyatakan ukuran
penyebaran vektor A . Perhatikan gambar sebagai contoh
pada kasus dua dimensi.

39. • gambar (a) memiliki divergensi yang sangat besar dan
positif (jika panahnya mengarah ke dalam berarti
nilainya negatif),
• gambar (b) memiliki divergensi nol,
gambar (c) memiliki divergensi positif yang nilainya• gambar (c) memiliki divergensi positif yang nilainya
agak kecil.

40. Curl
• Pemilihan nama curl juga disesuaikan dengan arti
geometrinya yang menyatakan ukuran rotasi pada
sebuah titik. Oleh karena itu seluruh fungsi pada gambar
divergensi memiliki curl yang bernilai nol (bisa kita cek
dengan mengetahui fungsinya) dan fungsi pada gambar
berikut memiliki curl yang sangat besar berarah padaberikut memiliki curl yang sangat besar berarah pada
sumbu-z.