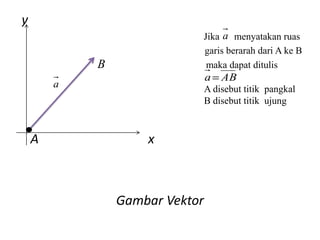
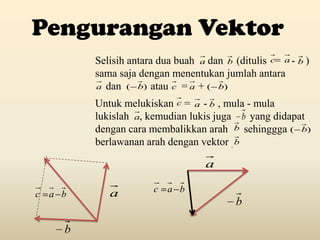
Dokumen ini membahas tentang vektor, termasuk penjumlahan dan pengurangan vektor dengan metode segitiga dan jajar genjang. Diberikan juga latihan dan tugas untuk menghitung operasi vektor dalam dimensi dua dan tiga. Kesimpulannya, penjumlahan dan pengurangan vektor dapat dilakukan dengan mengaplikasikan rumus yang sesuai untuk setiap dimensi.

1. ASSALAMUALAIKUM WR. WB

2. Sukses tak akan datang bagi mereka yg
hanya menunggu tak berbuat apa-apa, tapi
bagi mereka yang selalu berusaha
wujudkan mimpinya
Percayalah, hari ini akan lebih indah
Dari pada kemarin jika kita mengawalinya
dengan doa dan senyuman

3. OPERASI PADA VEKTOR:
penjumlahan dan pengurangan
By : Rahma Kusumaningtyas

4. Pernahkah kalian melihat lembing yang meluncur di udara saat
dilempar oleh atlet lempar lembing? Lembing tersebut meluncur
dengan kecepatan dan arah tertentu sesuai dengan keinginan
sang atlet. Dalam matematika, lembing yang meluncur ini mewakili
sebuah vektor, yaitu suatu besaran yang memiliki besar dan arah
Vektor adalah besaran yang
mempunyai besar dan arah

5. y
Jika a menyatakan ruas
garis berarah dari A ke B
B maka dapat ditulis
a AB
a A disebut titik pangkal
B disebut titik ujung
A x
Gambar Vektor

6. Penjumlahan Vektor
Metode Segitiga
y
b
a
a b c
x
Denga metode segitiga c didapat dengan cara
menghubungkan titik pangkal a dengan titik ujung b

7. Penjumlahan Vektor
• Metode Jajar genjang
y
a
a b c
x
b
Dengan metode jajar genjang, c didapat dengan cara
menghubungkan titik ujung a dengan titik ujung b

8. Pengurangan Vektor
Selisih antara dua buah a dan b (ditulis c= a - b )
sama saja dengan menentukan jumlah antara
a dan ( b) atau c = a + ( b)
Untuk melukiskan c = a - b , mula - mula
lukislah a, kemudian lukis juga b yang didapat
dengan cara membalikkan arah b sehinggga ( b)
berlawanan arah dengan vektor . b
a
a c a b
c a b
b
b

9. untuk a dan b vektordi R 2 berlaku:
a1 b1 a1 b1
a b
a2 b2 a2 b2
a1 b1 a1 b1
a b
a2 b2 a2 b2
dengan menggunakan pasangan berurutan,
dapat dituliskan :
a b (a1 , a2 ) (b1 , b2 ) (a1 b1 , a2 b2 )
a b (a1 , a2 ) (b1 , b2 ) (a1 b1 , a2 b2 )

10. untuk a dan b vektordi R3 berlaku:
a1 b1 a1 b1
a b a2 b2 a2 b2
a3 b3 a3 b3
a1 b1 a1 b1
a b a2 b2 a2 b2
a3 b3 a3 b3
dengan menggunakan pasangan berurutan,
dapat dituliskan :
a b (a1 , a2 , a3 ) (b1 , b2 , b3 ) (a1 b1 , a2 b2 , a3 b3 )
a b (a1 , a2 , a3 ) (b1 , b2 , b3 ) (a1 b1 , a2 b2 , a3 b3 )

11. Latihan:
1. Diketahui a (2, 3) , b (4, 5 ) dan c (1,3)
Hitunglah
(i ) a b
(ii) a b
(iii) a c
(iv) c a

12. TUGAS
1. Diketahui a (0, 2, 1) , b ( 2, 3, 4 ) dan c ( 3, 0, 3)
tentukan:
(i) a b (ii) c a
2.Diketahui a ( 4, 3) , b ( 2, 3 ) dan c (4, 8)
tentukan:
(i) b c (ii) a c (iii) ( a b) c
3. Diketahui a ( 5, 4, 3) , b (1, 2, 3 ) dan c ( 3, 8, 5)
tentukan:
(i) (a - b) ( a c)
(ii) (a - b) (a c)
Dikumpulka besuk saat istirahat pertama
n

13. Kesimpulan
untuk a dan b vektordi R 2
a b (a1 , a 2 ) (b1 , b2 ) (a1 b1 , a 2 b2 )
a b (a1 , a 2 ) (b1 , b2 ) (a1 b1 , a 2 b2 )
untuk a dan b vektordi R 3
a b (a1 , a 2 , a3 ) (b1 , b2 , b3 ) (a1 b1 , a 2 b2 , a3 b3 )
a b (a1 , a 2 , a3 ) (b1 , b2 , b3 ) (a1 b1 , a 2 b2 , a3 b3 )

14. WASSALAMUALAIKUM WR. WB