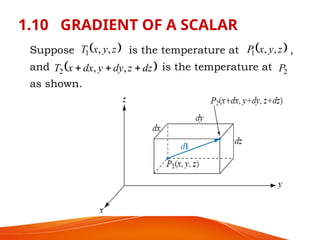
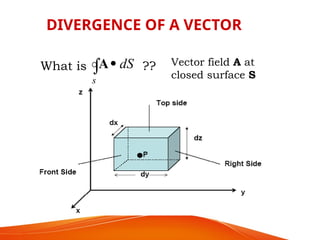
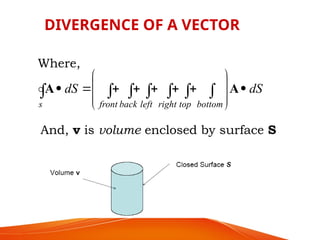
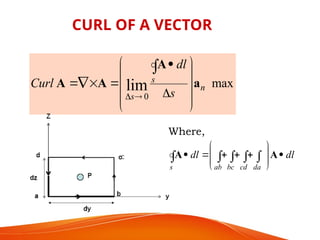
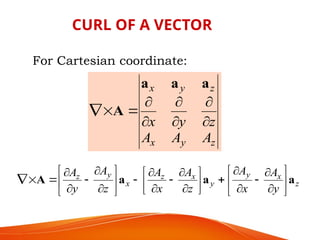
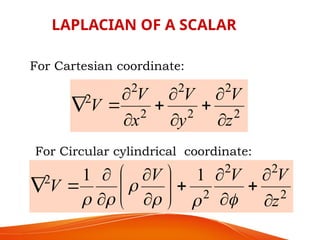
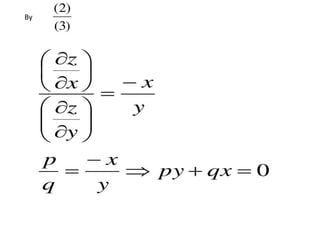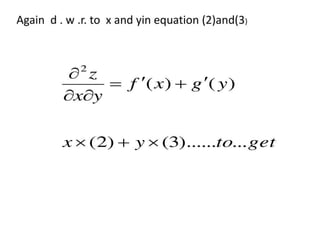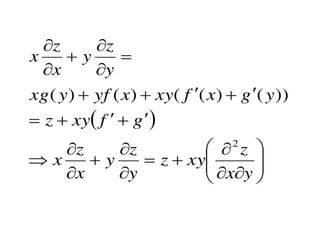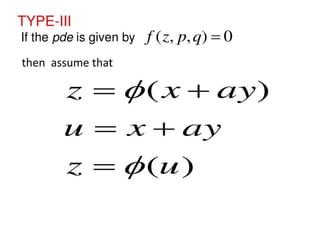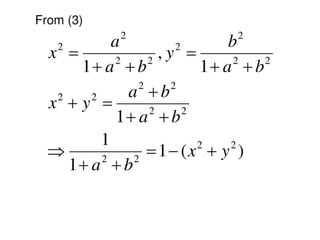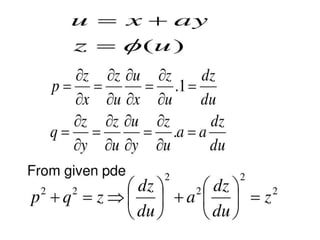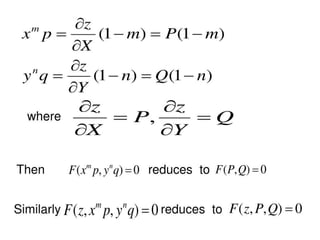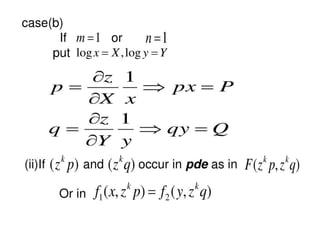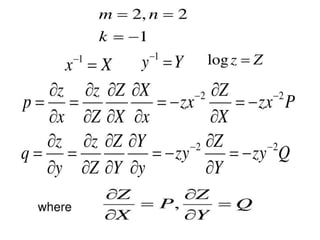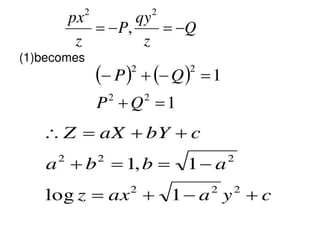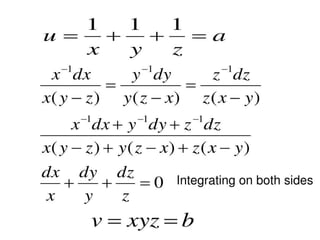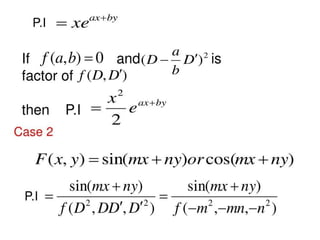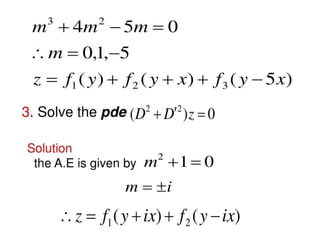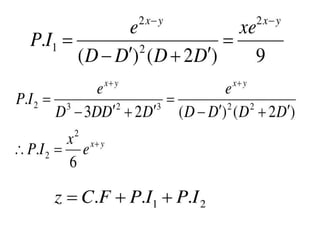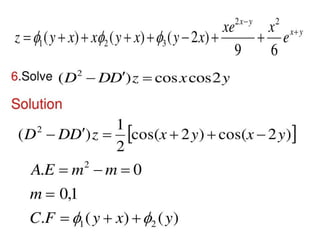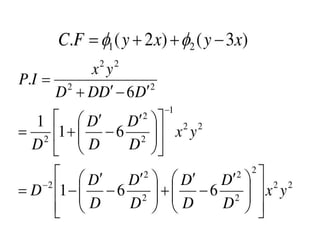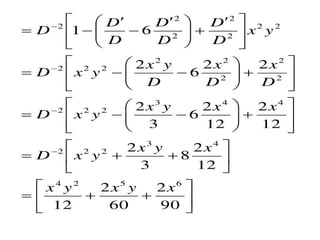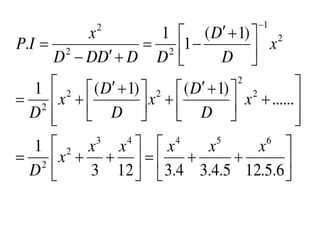The document is a PowerPoint presentation on differential equations, Laplace transforms, and vector analysis by M. Vijayalakshmi. It explains concepts such as ordinary and partial differential equations, their orders and degrees, and discusses vector analysis topics like gradient, divergence, curl, and the Laplacian in different coordinate systems. Key mathematical definitions and formulas related to these topics are also presented.

1. ODE,PDE,LAPLACE TRANSFORMS
AND VECTOR ANALYSIS
Power point presented by
M.VIJAYALAKSHMI M.Sc., M.Ed.,
Assistant Professor in Mathematics
Sri Sarada Niketan College of science for Women,Karur

2. Differential Equation
• a differential equation is an equation that
contains one or more functions with its
derivatives.
• The derivatives of the function define the rate of
change of a function at a point.
Example
2

3. Differential Equation
• Differential equation are two types namely
3
Differential Equation
Ordinary Differential
Equation
Partial Differential
Equation

4. Ordinary Differential Equation
• In a differential equation if there is a single
independent variable and the derivatives are
ordinary derivatives then it is called ordinary
differential equation.
Example
4

5. Partial Differential Equation
• If there are two or more independent variables
and the derivative are partial derivatives then it
is called a partial differential equation.
Example
5

6. Order
• The order of a differential equation is the order
of the “highest derivative” appearing in it.
Example
Here the order is 1
6

7. Degree
• The degree of the differential equation is the
“degree of the highest derivative” occurring in
it.
Example
Here degree is 1 & order is 1.
7

8. Homogeneous Equation
• A differential equation of first order and first
degree is said to be homogeneous.
• If it is can be put in the form
…………………..(1)
8

9. Homogeneous Equation(continue..)
Working Rule:
Let ie, …….(2)
Diff w.r.to x equ (2)
Then
Equ (1) becomes
9

10. Homogeneous Equation(continue..)
Separating x and v
…………………….(3)
Integrating equ (3)
After replace v by
10

11. Homogeneous Equation(continue..)
Exercise
Ans:
11

12. PARTIAL DIFFERENTIAL
EQUATIONS

77. VECTOR ANALYSIS
 GRADIENT OF A SCALAR
 DIVERGENCE OF A VECTOR
 DIVERGENCE THEOREM
 CURL OF A VECTOR
 LAPLACIAN OF A SCALAR

78. 1.10 GRADIENT OF A SCALAR
Suppose is the temperature at ,
and is the temperature at
as shown.
 
z
y
x
T ,
,
1  
z
y
x
P ,
,
1
2
P
 
dz
z
dy
y
dx
x
T 

 ,
,
2

79. The differential distances are the
components of the differential distance
vector :
dz
dy
dx ,
,
z
y
x dz
dy
dx
d a
a
a
L 


L
d
However, from differential calculus, the
differential temperature:
dz
z
T
dy
y
T
dx
x
T
T
T
dT










 1
2
GRADIENT OF A SCALAR

80. But,
z
y
x
d
dz
d
dy
d
dx
a
L
a
L
a
L






So, previous equation can be rewritten as:
L
a
a
a
L
a
L
a
L
a
d
z
T
y
T
x
T
d
z
T
d
y
T
d
x
T
dT
z
y
x
z
y
x






























GRADIENT OF A SCALAR

81. The vector inside square brackets defines the
change of temperature corresponding to a
vector change in position .
This vector is called Gradient of Scalar T.
L
d
dT
GRADIENT OF A SCALAR
For Cartesian coordinate:
z
y
x
z
V
y
V
x
V
V a
a
a











82. The vector inside square brackets defines the
change of temperature corresponding to a
vector change in position .
This vector is called Gradient of Scalar T.
L
d
dT
GRADIENT OF A SCALAR
For Cartesian coordinate:
z
y
x
z
V
y
V
x
V
V a
a
a











83. 1.11 DIVERGENCE OF A VECTOR
Illustration of the divergence of a vector
field at point P:
Positive
Divergence
Negative
Divergence
Zero
Divergence

84. DIVERGENCE OF A VECTOR
The divergence of A at a given point P
is the outward flux per unit volume:
v
dS
div s
v 








A
A
A lim
0

85. DIVERGENCE OF A VECTOR
What is ??
 
s
dS
A Vector field A at
closed surface S

86. Where,
dS
dS
bottom
top
right
left
back
front
s















 





 A
A
And, v is volume enclosed by surface S
DIVERGENCE OF A VECTOR

87. For Cartesian coordinate:
z
A
y
A
x
A z
y
x










 A
For Circular cylindrical coordinate:
  z
A
A
A z


















1
1
A
DIVERGENCE OF A VECTOR

88. 1.13 CURL OF A VECTOR
The curl of vector A is an axial
(rotational) vector whose magnitude is
the maximum circulation of A per unit
area tends to zero and whose direction
is the normal direction of the area
when the area is oriented so as to
make the circulation maximum.

89. max
lim
0
a
A
A
A n
s
s s
dl
Curl



















Where,
CURL OF A VECTOR
dl
dl
da
cd
bc
ab
s













 



 A
A

90. CURL OF A VECTOR
The curl of the vector field is concerned
with rotation of the vector field. Rotation
can be used to measure the uniformity
of the field, the more non uniform the
field, the larger value of curl.

91. For Cartesian coordinate:
CURL OF A VECTOR
z
y
x
z
y
x
A
A
A
z
y
x 








a
a
a
A
z
x
y
y
x
z
x
y
z
y
A
x
A
z
A
x
A
z
A
y
A
a
a
a
A 






































92. z
z
A
A
A
z








 








a
a
a
A
1
 
z
z
z
A
A
z
A
A
z
A
A
a
a
a
A



















































1
1
For Circular cylindrical coordinate:
CURL OF A VECTOR

93. CURL OF A VECTOR
For Spherical coordinate:
  







A
r
rA
A
r
r
r
r
sin
sin
1
2









a
a
a
A
   
 













a
a
a
A










































r
r
r
A
r
rA
r
r
rA
A
r
A
A
r
)
(
1
sin
1
1
sin
sin
1

94. 1.15 LAPLACIAN OF A SCALAR
The Laplacian of a scalar field, V
written as:
V
2

Where, Laplacian V is:



































z
y
x
z
y
x
z
V
y
V
x
V
z
y
x
V
V
a
a
a
a
a
a
2

95. For Cartesian coordinate:
2
2
2
2
2
2
2
z
V
y
V
x
V
V










For Circular cylindrical coordinate:
2
2
2
2
2 1
1
z
V
V
V
V
























LAPLACIAN OF A SCALAR

96. LAPLACIAN OF A SCALAR
For Spherical coordinate:
2
2
2
2
2
2
2
2
sin
1
sin
sin
1
1
































V
r
V
r
r
V
r
r
r
V

97. 97
THANK YOU