Uploaded byGHSKassKoronaMardan
83 views

Graddivcurl1

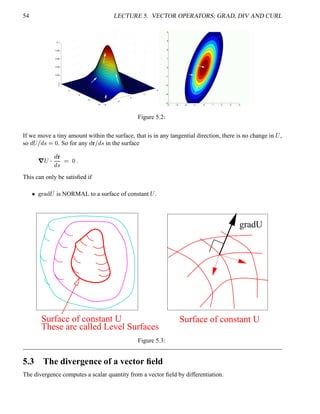
The document introduces three vector field operators: the gradient, divergence, and curl. The gradient of a scalar field points in the direction of greatest change and represents the directional derivative. The divergence represents the flux generation per unit volume and is a measure of the efflux from an infinitesimal volume. The curl represents the circulation of a vector field around an infinitesimal loop or surface and is related to rotational properties of the field. Examples are provided to demonstrate calculating each operator.

Embed presentation

Download to read offline
Lecture 5 Vector Operators: Grad, Div and Curl In the first lecture of the second part of this course we move more to consider properties of fields. We introduce three field operators which reveal interesting collective field properties, viz.   the gradient of a scalar field,   the divergence of a vector field, and   the curl of a vector field. There are two points to get over about each:   The mechanics of taking the grad, div or curl, for which you will need to brush up your multivariate calculus.   The underlying physical meaning — that is, why they are worth bothering about. In Lecture 6 we will look at combining these vector operators. 5.1 The gradient of a scalar field Recall the discussion of temperature distribution throughout a room in the overview, where we wondered how a scalar would vary as we moved off in an arbitrary direction. Here we find out how to. If ¡£¢¥¤§¦©¨¦ is a scalar field, ie a scalar function of position ¤§¦©¨¦ in 3 dimensions, then its gradient at any point is defined in Cartesian co-ordinates by !#©$ % ¡ ¡ ¤(')10 ¡ ¨1'230 ¡ '465 It is usual to define the vector operator 7 ') ¤ 0 '2 ¨ 0 '4 which is called “del” or “nabla”. Then !#©$ % ¡98@7A¡ 51
52 LECTURE 5. VECTOR OPERATORS: GRAD, DIV AND CURL Note immediately that 7A¡ is a vector field! Without thinking too carefully about it, we can see that the gradient tends to point in the direction of greatest change of the scalar field. Later we will be more precise.   Worked examples of gradient evaluation 1. ¡ ¤¢¡ Only ¤£ ¤ exists so 7A¡ ¦¥ ¤ ') 5 2. ¡ ¨§ ¡ § ¡ ¤¢¡ 0 ¨©¡ 0 ¡ , so 7A¡ ¥ ¤ ') 0 ¥ ¨ '2 0 ¥ '4 ¥ 5 3. ¡ , where is constant. 7A¡ ') ¤ 0 '2 ¨ 0 '4 ¢! ¤ 0 ¡ ¨ 0 # ! ') 0 ¡ '2 0 $ '4 ¨ 5 4. ¡ ¦% ¢ § ¡ % ¢¤ §¦©¨¦ ¦% ¢ § ¢¤ §¦©¨¦ Now #' )( 102' 043 )3 $( , #' )5 106' 073 )3 )5 , and #' $8 902' 043 )3 #8 , so 7A¡ % ¤ ') 0 % ¨ '2 0 % '4 A@ % @ §CB § ¤ ') 0 § ¨ '2 0 § '4ED But § GF ¤ ¡ 0 ¨ ¡ 0 ¡ , so § £ ¤ ¤ £ § and similarly for ¨ ¦ . Hence 7A¡ @ % @ §HB § ¤ ') 0 § ¨ '2 0 § '4 D @ % @ §PI ¤ ') 0 ¨ '2 0 '4 § Q @ % @ §SR §¤T 5
5.2. THE SIGNIFICANCE OF GRAD 53 grad  ¡£¢¥¤¦¡¨§  © ¡¢¤¦¡ ¡¦§  © ¡ ¤¦¡ Figure 5.1: The directional derivative 5.2 The significance of grad We have seen that 7A¡ ¡ ¤ ') 0 ¡ ¨ '2 0 ¡ '4 so if we move a small amount @ @ ¤ ') 0 @ ¨ '2 0 @ '4 the change in ¡ is (see figure 5.1) @ ¡ ¡ ¤ @ ¤ 0 ¡ ¨ @ ¨ 0 ¡ @ 7A¡ @ 5 Now divide by @ @ ¡ @ 7 ¡ @ @ 5 But remember that @ @ , so @ £ @ is a unit vector in the direction of @ . So   !#©$ % ¡ has the property that the rate of change of ¡ wrt distance in a particular direction ( ' ) is the projection of !# $ % ¡ onto that direction (or the component of ! ©$ % ¡ in that direction). The quantity @ ¡ £ @ is called a directional derivative. Note that in general it has a different value for each direction, and so has no meaning until you specify the direction. We could also say that   At any point P, !#©$ % ¡ points in the direction of greatest change of ¡ at P, and has magnitude equal to the rate of change of ¡ wrt distance in that direction. Another nice property emerges if we think of a surface of constant ¡ – that is the locus ¢¤ §¦©¨¦ for ¡£¢¥¤§¦©¨¦ !$#%' $ #(
54 LECTURE 5. VECTOR OPERATORS: GRAD, DIV AND CURL −4 −2 0 2 4 −4 −2 0 2 4 0 0.02 0.04 0.06 0.08 0.1 Figure 5.2: If we move a tiny amount within the surface, that is in any tangential direction, there is no change in ¡ , so @ ¡ £ @ ¡  . So for any @ £ @ in the surface 7A¡ @ @   5 This can only be satisfied if   ! ©$ % ¡ is NORMAL to a surface of constant ¡ . Surface of constant U gradU Surface of constant U These are called Level Surfaces Figure 5.3: 5.3 The divergence of a vector field The divergence computes a scalar quantity from a vector field by differentiation.
5.4. THE SIGNIFICANCE OF  ¢¡¤£ 55 More precisely, if ¥ ¢¥¤§¦©¨¦ is a vector function of position in 3 dimensions, that is ¥ §¦ ')0 ¦ ¡ '2 0 ¦ '4 , then its divergence at any point is defined in Cartesian co-ordinates by %©¨ ¥ ¦ ¤ 0 ¦ ¡ ¨ 0 ¦ We can write this in a simplified notation using a scalar product with the 7 vector differential operator: %©¨ ¥ ') ¤ 0 '2 ¨ 0 '4 ¥ 7 ¥ Notice that the divergence of a vector field is a scalar field.   Worked examples of divergence evaluation ¥ div¥¤ ') ¢ ¤ ') 0 ¨ '2 0 '4 3   § ¢ £ § where is constant Let us show the third example. The ¤ component of £ § is ¤ 5¢ ¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ , and we need to find £ ¤ of it. ¤ ¤ 5¢ ¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ 5¢ ¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ 0 ¤! ¥ ¢¥¤ ¡ 0 ¨ ¡ 0 ¡ # ¡ 5¥ ¤ § %$ ¤ ¡ § ¡ Adding this to similar terms for ¨ and gives § $ ¢¤ ¡ 0 ¨ ¡ 0 ¡ § ¡ § ¢' # ¡  5.4 The significance of (0)21 Consider a typical vector field, water flow, and denote it by ¥ ¢ . This vector has magnitude equal to the mass of water crossing a unit area perpendicular to the direction of ¥ per unit time. Now take an infinitesimal volume element @#3 and figure out the balance of the flow of ¥ in and out of @43 . To be specific, consider the volume element @43 @ ¤ @ ¨ @ in Cartesian co-ordinates, and think first about the face of area @ ¤ @ perpendicular to the ¨ axis and facing outwards in the negative ¨ direction. (That is, the one with surface area @65 @ ¤ @ '2 .) The component of the vector ¥ normal to this face is ¥ '2 7¦ 5 , and is pointing inwards, and so the its contribution to the OUTWARD flux from this surface is ¥ @©5 ¦ 5 ¢ ¨ @ @ ¤ 5 (Flux here means mass per unit time.)
56 LECTURE 5. VECTOR OPERATORS: GRAD, DIV AND CURL dS = -dxdz j y x z dz dx dy jdS = +dxdz Figure 5.4: Elemental volume for calculating divergence. A similar contribution, but of opposite sign, will arise from the opposite face, but we must remember that we have moved along ¨ by an amount @ ¨ , so that this OUTWARD amount is ¦ 5 ¢¨ 0 @ ¨ @ @ ¤ ¦ 5 0 ¦ 5 ¨ @ ¨ @ ¤ @ The total outward amount from these two faces is ¦ 5 ¨ @ ¨ @ ¤ @ ¦ 5 ¨ @#3 Summing the other faces gives a total outward flux of ¦ ( ¤ 0 ¦ 5 ¨ 0 ¦ 8 @#3 7 ¥ @#3 Take home message: The divergence of a vector field represents the flux generation per unit volume at each point of the field. (Divergence because it is an efflux not an influx.) Interestingly we also saw that the total efflux from the infinitesimal volume was equal to the flux inte- grated over the surface of the volume. (NB: The above does not constitute a rigorous proof of the assertion because we have not proved that the quantity calculated is independent of the co-ordinate system used, but it will suffice for our purposes. 5.5 The Laplacian: (0)21 ¡£¢¥¤§¦ (©¨ of a scalar field Recall that !# $ % ¡ of any scalar field ¡ is a vector field. Recall also that we can compute the divergence of any vector field. So we can certainly compute %©¨ ¢ ! ©$ % ¡ , even if we don’t know what it means yet.
5.5. THE LAPLACIAN:  ¢¡¤£ ¢¡ £¢¥¤   ¡ OF A SCALAR FIELD 57 Here is where the 7 operator starts to be really handy. 7 ¢ 7 ¡ ') ¤ 0 '2 ¨ 0 '4 ') ¤ 0 '2 ¨ 0 '4 ¡ ') ¤ 0 '2 ¨ 0 '4 ') ¤ 0 '2 ¨ 0 '4 ¡ ¡ ¤ ¡ 0 ¡ ¨ ¡ 0 ¡ ¡ ¡ ¡ ¡ ¤ ¡ 0 ¡ ¡ ¨ ¡ 0 ¡ ¡ ¡ This last expression occurs frequently in engineering science (you will meet it next in solving Laplace’s Equation in partial differential equations). For this reason, the operator ¦ ¡ is called the “Laplacian” ¦ ¡ ¡ ¡ ¤ ¡ 0 ¡ ¨ ¡ 0 ¡ ¡ ¡ Laplace’s equation itself is ¦ ¡ ¡     Examples of §©¨ evaluation § ¨ ¨¨!#$¨%'(¨0) 1 ¨ 32 456327'1(8 ¨ 9A@ B Let’s prove the last example (which is particularly significant – can you guess why?). £ § ¢¥¤¢¡ 0 ¨©¡ 0 ¡ ' ¡ and so ¤ ¤ ¢¥¤ ¡ 0 ¨ ¡ 0 ¡ ' ¡ ¤ ¤ 5¢¤ ¡ 0 ¨ ¡ 0 ¡ ¡ ¢¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ 0 ¤ 5¤ 5¢¤ ¡ 0 ¨ ¡ 0 ¡ # ¡ ¢ £ § ¢ 0 ¤ ¡ £ § ¡ Adding up similar terms for ¨ and ¦ ¡ § § 0 ¢¥¤¢¡ 0 ¨ ¡ 0 ¤¢¡ § ¡  
58 LECTURE 5. VECTOR OPERATORS: GRAD, DIV AND CURL 5.6 The curl of a vector field So far we have seen the operator 7   Applied to a scalar field 7 ¡ ; and   Dotted with a vector field 7 ¥ . You are now overwhelmed by that irrestible temptation to   cross it with a vector field 7   ¥ This gives the curl of a vector field 7¡  ¥ 8 £¢ ¥¤¢ ¥ We can follow the pseudo-determinant recipe for vector products, so that 7¡  ¥ ¦¦¦¦¦¦ ') '2 '4 )( )5 $8¦ ( ¦ 5 ¦ 8 ¦¦¦¦¦¦ ¦ 8 ¨ ¦ 5 ') 0 ¦ ( ¦ 8 ¨ '2 0 ¦ 5 ¤ ¦ ( ¨ '4   Examples of curl evaluation ¥ 7§  ¥ ¨ ') 0 ¤ '2 ¥ '4 ¤¢¡¨©¡ '4 ¥ ¤¢¡¨ ') ¥ ¤ ¨©¡ '2 5.7 The signficance of curl Perhaps the first example gives a clue. The field ¥ ¨ ') 0 ¤ '2 is sketched in Figure 5.5(a). (It is the field you would calculate as the velocity field of an object rotating with ¨   ¦   ¦ .) This field has a curl of ¥ '4 , which is in the r-h screw out of the page. You can also see that a field like this must give a finite value to the line integral around the complete loop © ¥ @ 5 In fact curl is closely related to the line integral around a loop. The circulation of a vector ¥ round any closed curve is defined to be ¥ @ and the curl of the vector field ¥ represents the vorticity, or circulation per unit area, of the field. Our proof uses the small rectangular element @ ¤ by @ ¨ shown in Figure 5.5(b). Consider the circulation round the perimeter of a rectangular element.
5.8. SOME DEFINITIONS INVOLVING DIV, CURL AND GRAD 59 y x ax(y) a(x)y ax(y+dy) ay(x+dx) dx dy y y x x+dx y+dy Figure 5.5: (a) A rough sketch of the vector field ¨ ') 0 ¤ '2 . (b) An element in which to calculate curl. The fields in the ¤ direction at the bottom and top are ¦ ( ¢ ¨ $ # % ¦ ( ¢¥¨ 0 @ ¨ ¦ ( ¢¥¨ 0 ¦ ( ¨ @ ¨ and the fields in the ¨ direction at the left and right are ¦ 5 ¢¤ $ # % ¦ 5 ¢¤ 0 @ ¤ §¦ 5 ¢¤ 0 ¦ 5 ¤ @ ¤ Starting at the bottom and working round in the anticlockwise sense, the four contributions to the circu- lation @ are therefore as follows, where the minus signs take account of the path being oppose to the field: @ 0 ¦ ( ¢ ¨ @ ¤ 0 ¦ 5 ¢¥¤ 0 @ ¤ @ ¨ ¦ ( ¢ ¨ 0 @ ¨ @ ¤ ¦ 5 ¢¤ @ ¨ 0 ¦ ( ¢ ¨ @ ¤ 0 B ¦ 5 ¢¤ 0 ¦ 5 ¤ @ ¤ @ ¨ D B ¦ ( ¢¥¨ 0 ¦ ( ¨ @ ¨ @ ¤ D ¦ 5 ¢¤ @ ¨ ¦ 5 ¤ ¦ ( ¨ @ ¤ @ ¨ ¢ 7§  ¥ @65 where @65 @ ¤ @ ¨ '4 . NB: Again, this is not a completely rigorous proof as we have not shown that the result is independent of the co-ordinate system used. 5.8 Some definitions involving div, curl and grad   A vector field with zero divergence is said to be solenoidal.   A vector field with zero curl is said to be irrotational.   A scalar field with zero gradient is said to be, er, well, constant. IDR October 21, 2003
60 LECTURE 5. VECTOR OPERATORS: GRAD, DIV AND CURL
Lecture 6 Vector Operator Identities In this lecture we look at more complicated identities involving vector operators. The main thing to appreciate it that the operators behave both as vectors and as differential operators, so that the usual rules of taking the derivative of, say, a product must be observed. We shall derive these using both conventional grunt, and using the compact notation. Note that the relevance of these identities may only become clear later in other Engineering courses. 6.1 Identity 1: curl grad ¨ =   ¡   ¨ ¢ £ 7§  7A¡ ¦¦¦¦¦¦ ') '2 '4 ¤£ ¤ ¤£ ¨ ¤£ ¡ £ ¤ ¡ £ ¨ ¡ £ ¦¦¦¦¦¦ ') ¡ ¡ ¨ ¡ ¡ ¨ 0 '2 ¢ 0 '4 ¢ ¤ 5 Note that 7¡  7 can be thought of as a null operator. 6.2 Identity 2: div curl ¥ =   ¦§  ¡ ¥¨¢ © 7 7§  ¥ ¦¦¦¦¦¦ £ ¤ ¤£ ¨ ¤£ £ ¤ ¤£ ¨ ¤£ ¦ ( ¦ 5 ¦ 8 ¦¦¦¦¦¦ ¡ ¦ 8 ¤ ¨ ¡ ¦ 5 ¤ ¡ ¦ 8 ¨ ¤ 0 ¡ ¦ ( ¨ ¡ ¦ 5 ¤ ¡ ¦ ( ¨   61
62 LECTURE 6. VECTOR OPERATOR IDENTITIES 6.3 Identity 3: div and curl of ¨ ¥ Suppose that ¡£¢ is a scalar field and that ¥ ¢ is a vector field and we are interested in the product ¡ ¥ , which is a vector field so we can compute its divergence and curl. For example the density ¡ ¢ of a fluid is a scalar field, and the instantaneous velocity of the fluid ¢ ¢ is a vector field, and we are probably interested in mass flow rates for which we will be interested in ¡ ¢ ¢ ¢ . The divergence (a scalar) of the product ¡ ¥ is given by: 7 ¢ ¡ ¥ 7 ¢ ¡ ¥ ¡£¢ 7 ¥ 0 ¢ 7 ¡ ¥ ¡ %©¨ ¥ 0 ¢ !#©$ % ¡ ¥ In a similar way, we can take the curl of the vector field ¡ ¥ , and the result should be a vector field: 7¡  ¢ ¡ ¥ ¡ 7§  ¥ 0 ¢ 7A¡   ¥ 5 6.4 Identity 4: div of ¥ ¡ £ Life quickly gets trickier when vector or scalar products are involved: For example, it is not that obvious that %6¨ ¢ ¥  ¥¤ £¢ ¥¤¥ ¤ ¥ £¢ ¥¤¤ To show this, use the determinant: ¦¦¦¦¦¦ £ ¤§¦ £ ¤©¨ ¤£ ¤ ¦ ( ¦ 5 ¦ 8 ( 5 8 ¦¦¦¦¦¦ ¤ ¦ 5 8 ¦ 8 5 0 ¨ ¦ 8 ( ¦ ( 8 0 ¦ ( 5 ¦ 5 ( 5 5 5 $ % ! ¢ ! % ¢% 5 5 5 £¢ ¥¤¥ ¤ ¥ ¢ curl ¤ 6.5 Vector operator identities in HLT There is a kind of cottage industry in inventing vector identities. HLT contains a lot of them. So why not leave it at that? First, since !#©$ % , %©¨ and ¢ ¤ describe key aspects of vectors fields, they arise often in practice, and so the identities can save you a lot of time and hacking of partial derivatives, as we will see when we consider Maxwell’s equation as an example later. Secondly, they help to identify other practically important vector operators. We now look at such an example.
6.6. IDENTITY 5:  ¢¡ ¢¤£ ¢¦¥  ¨§ 63 6.6 Identity 5: © ¤ ¡ ¥ ¡ £ £¢ ¥¤¢ ¥  ¥¤ ¦¦¦¦¦¦ ') '2 '4 ¤£ ¤ £ ¨ ¤£ ¦ 5 8 ¦ 8 5 ¦ 8 ( ¦ ( 8 ¦ ( 5 ¦ 5 ( ¦¦¦¦¦¦ so the ') component is ¨ ¢ ¦ ( 5 ¦ 5 ( ¢ ¦ 8 ( ¦ ( 8 which can be written as the sum of four terms: ¦ ( 5 ¨ 0 8 D ( ¦ 5 ¨ 0 ¦ 8 D 0 5 ¨ 0 8 ¦ ( ¦ 5 ¨ 0 ¦ 8 ( Adding ¦ ( )( to the first of these, and subtracting from the last, and doing the same with ( )( to the other two terms, we find that: 7§  ¢ ¥   ¤ ¢ 7 ¤ ¥ ¢ 7 ¥ ¤ 0 ¤ 76 ¥ ¥ 7 ¤ where ¥ 76 can be regarded as new, and very useful, scalar differential operator. 6.7 Definition of the operator ¥ ¦§  ! This is a scalar operator, but it can obviously can be applied to a scalar field, resulting in a scalar field, or to a vector field resulting in a vector field: ¥ 7 8 B ¦ ( ¤ 0 ¦ 5 ¨ 0 ¦ 8 D 5 6.8 Identity 6: © ¤ ¡ © ¤ ¥ for you to derive The following important identity is stated, and let as an exercise: £¢ ¥¤¢ £¢ ¥¤¥ ! ©$ % %©¨ ¥ ¦ ¡ ¥ where ¦ ¡ ¥ ¦ ¡ ¦ ( ') 0 ¦ ¡ ¦ 5 '2 0 ¦ ¡ ¦ 8 '4   Example of Identity 6: electromagnetic waves Background: Maxwell established a set of four vector equations which are fundamental to working out how eletromagnetic waves propagate. The entire telecommunications industry is built on these! %©¨$# ¡ %©¨ §   £¢ ¤% (' § £¢ ¥¤0) 1 0 (' #
64 LECTURE 6. VECTOR OPERATOR IDENTITIES In addition, we can assume the following § ¡  3  £¢ ) , 1 ¥¤ % , # ¡¦ 3 ¦§¢ % , where all the scalars are constants. Question: Show that in a material with no free charge, ¡   , and with zero conductivity, ¤   , the eletric field % must be a solution of the wave equation ¦ ¡ % ¡  3  £¢¨¦ 3 ¦§¢ ¢ ¡ % £ (' ¡ 5 Answer: The good news is that we can do this knowing little about EM waves! %6¨$# %©¨ ¢ ¦ 3 ¦§¢ % ©¦ 3 ¦¢ %©¨ % ¡  %©¨ § %©¨ ¢   3  £¢ ) ¥  3  £¢ %6¨$)   £¢ ¥¤% § £ ('   3  £¢ ¢ ) £ (' ¢ ¤) 1 0 # £ (' ¤ 0 ¦ 3 ¦§¢ ¢ % £ (' But we know (or rather you worked out) that £¢ ¤£¢ ¥¤0% !# $ % %©¨ $% ¦ ¡ % , so ¢ ¤£¢ ¤0% ¢ ¤   3  ¢ ¢ ) £ (' !#©$ % %©¨ (% ¦ ¡ % so interchanging the order of partial differentation, and using %©¨ $%   :   3  £¢ (' ¢ ¤0) ¦ ¡ %   3  £¢ (' B ¦ 3 ¦§¢ % (' D ¦ ¡ %   3  £¢¨¦ 3 ¦§¢ ¡ % (' ¡ ¦ ¡ % 6.9 Grad, div, curl and ¥ in curvilinear co-ordinate systems It is possible to obtain general expressions for grad, div and curl in any orthogonal curvilinear co-ordinate system by making use of the factors which were introduced in Lecture 4. We recall that the unit vector in the direction of increasing , with and being kept constant, is where is the radius vector, and ¦¦¦¦ ¦¦¦¦ and similar expressions apply for the other co-ordinate directions. Then @ © @ 0 ! ¢ @ 0 # @ 5
6.10. GRAD IN CURVILINEAR COORDINATES 65 6.10 Grad in curvilinear coordinates Using the properties of the gradient of a scalar field obtained previously, 7A¡ @ @ ¡ ¡ @ 0 ¡ @ 0 ¡ @ It follows that 7A¡ ¢ @ 0 ! ¢ @ 0 # @ ¡ @ 0 ¡ @ 0 ¡ @ The only way this can be satisfied for independent @ , @ , @ is when 7A¡ ¡ ' 0 ! ¡ '¢ 0 ¡ '# 6.11 Divergence in curvilinear coordinates Expressions can be obtained for the divergence of a vector field in orthogonal curvilinear co-ordinates by making use of the flux property. We consider an element of volume @#3 . Although earlier we derived this as the volume of a parallelop- iped, and found that the @#3 ¦¦¦¦ ¢¥¤§¦©¨¦ ¢ ¦ ¦ ¦¦¦¦ @ @ @ If the curvilinear coordinates are orthogonal then the little volume is a cuboid (to first order in small quantities) and @#3 ¡ ! @ @ @ 5 However, it is not quite a cuboid: the area of two opposite faces will differ as the scale parameters are functions of , and in general. So the net efflux from the two faces in the '¢ direction shown in Figure 6.1 is B ¦ ! 0 ¦ ! @ D B 0 @ D B 0 @ D @ @ ¦ ! @ @ ¢ ¦ ! @ @ @ which is easily shown by multiplying the first line out and dropping second order terms (i.e. ¢ @ $¡ ). By definition div is the net efflux per unit volume, so summing up the other faces: %©¨ ¥ @#3 ¢ ¦ ! 0 ¢ ¦ ! 0 ¢ ¦ ! @ @ @ ¡ %6¨ ¥ ! @ @ @ ¢ ¦ ! 0 ¢ ¦ ! 0 ¢ ¦ ! @ @ @
66 LECTURE 6. VECTOR OPERATOR IDENTITIES w u y The scale params are h (v) dw h (v+dv) dw h (v+dv) du h (v) du u w w u h dvv functions of u,v,w Figure 6.1: Elemental volume for calculating divergence in orthogonal curvilinear coordinates So, finally, %6¨ ¥ ! ¢ ¦ ! 0 ¢ ¦ ! 0 ¢ ¦ ! 6.12 Curl in curvilinear coordinates Recall from Lecture 5 that we computed the component of curl as the circulation per unit area — the contents of the brackets ¢ in the expression for the element of circulation @ ¦ 5 ¤ ¦ ( ¨ @ ¤ @ ¨ By analogy with our derivation of divergence, you will realize that for an orthogonal curvilinear coordi- nate system we can write the area as ! @ @ . But the opposite sides are no longer quite of the same length. The lower of the pair in Figure 6.2 is length ¢ @ , but the upper is of length ¢ 0 @ @ Summing this pair gives a contribution to the circulation ¦ ¢ ¢ @ ¦ ¢ 0 @ ¢ 0 @ @ ¢ ¦ @ @ and together with the other pair: @ ¢ ¦ 0 ¢ ! ¦ ! @ @ So the circulation per unit area is @ ! @ @ ! ¢ ! ¦ ! ¢ ¦
6.13. THE LAPLACIAN IN CURVILINEAR COORDINATES 67 y y a a u u u+du u u u v+dv (v+dv) h (v+dv) du dv (v) h (v) du Figure 6.2: Elemental loop for calculating curl in orthogonal curvilinear coordinates and hence curl is £¢ ¥¤¥ ¢ ¦ ¦ ! ¢ ¦ ¢ ! ¦ ! ' 0 ¢ ¦ ¢ ¦ '¢ 0 ! ¢ ! ¦ ! ¢ ¦ '# 6.13 The Laplacian in curvilinear coordinates Substitution of the components of !#©$ % ¡ into the expression for %©¨ ¥ immediately (!*?) gives the following expression for the Laplacian in general orthogonal co-ordinates: ¦ ¡ ¡ ! B ! ¡ 0 ! ¡ 0 ! ¡ D 5 6.14 Grad, etc, in cylindrical polars We recall that § ! %¡  ') 0 §% ¨ #¢  '2 0 '4 , and that £ , and so F ¢ !$% ¡   0 ¤£¦¥ ¡   ¦ ¡ § ¢ § ¡ % ¨ # ¡   0 § ¡ ! % ¡   § ¦
68 LECTURE 6. VECTOR OPERATOR IDENTITIES Hence ! ©$ % ¡ ¡ § '  3 0 § ¡   ' ¢¡ 0 ¡ '4 %©¨ ¥ § ¢ § ¦ 3 § 0 ¦ ¡   0 ¦ 8 £¢ ¥¤¥ § ¦ 8   ¦ ¡ '  3 0 ¦ 3 ¦ 8 § ' ¢¡ 0 § ¢ § ¦ ¡ § ¦ 3   '4 The derivation of the expression for ¦ ¡ ¡ in cylindrical polar co-ordinates is set as a tutorial exercise. 6.15 Grad, etc, in spherical polars We recall that ¨§% ¨ #¤£ !$%¡  ') 0 § % ¨ #¤£ % ¨ #   '2 0 § !$%¥£ '4 so that § ¢ % ¨ # ¡ £ ¢ ! % ¡   0 % ¨ # ¡   0 !$% ¡ £ ¡ § ¢ § ¡ ! % ¡ £ ¢ !$% ¡   0 % ¨ # ¡   0 § ¡ % ¨ # ¡ £ § § ¢ § ¡ % ¨ # ¡ £ ¢ % ¨ # ¡   0 !$% ¡   ¨§ % ¨ #¤£ Hence ! ©$ % ¡ ¡ § '  3 0 § ¡ £ ' ¢¦ 0 § % ¨ #§£ ¡   ' ¨¡ %©¨ ¥ § ¡ ¢ § ¡ ¦ 3 § 0 § % ¨ #§£ ¢ ¦ ¦ % ¨ #§£ £ 0 § % ¨ #§£ ¦ ¡   £¢ ¥¤¥ '  3 § % ¨ #§£ £ ¢ ¦ ¡ % ¨ #§£   ¢ ¦ ¦ 0 ' ¢¦ §% ¨ #¤£   ¢ ¦ 3 § ¢ ¦ ¡ § % ¨ #¤£ 0 ' ¢¡ § § ¢ ¦ ¦ § £ ¢ ¦ 3   The derivation of the expression for ¦ ¡ ¡ is set as a tutorial exercise.   Examples Q1 Find ¢ ¤¥ in (i) Cartesians and (ii) Spherical poplars when ¥ ¤ ¢¥¤ ') 0 ¨ '2 0 '4 .
6.15. GRAD, ETC, IN SPHERICAL POLARS 69 A1 (i) In Cartesians, using the pseudo determinant gives ¢ ¤¥ '2 0 ¨ '4 . (ii) By inspection, in spherical polars ¥ § % ¨ #¤£ ! %¡  ¢ § '  3 so ¦ 3 ¨§ ¡ % ¨ #¤£ !$%¡ ¡  ¦ ¦ ¡ ¢  ¦ ¡   5 Hence £¢ ¤¥ ' ¨¦ §% ¨ #¤£   ¢ § ¡ % ¨ #¤£ !$%¡  0 ' ¢¡ § £ ¢ § ¡ % ¨ #§£ !$%   ' ¨¦ §% ¨ #¤£ ¢ § ¡ % ¨ #§£ % ¨ #   0 ' ¢¡ § $ § ¡ !$% £ !$%   ' ¢¦ ¢ §% ¨ #¢  0 ' ¢¡ ¢ § !$%¥£ !$%¡  Now, these two results should be the same, but to check we need expressions for '  3 etc in terms of ') etc. Remember that we can work out the unit vectors '  3 and so on in terms of ') etc using '  3 @ §   ' ¢¦ ¡ @ £   ' ¢¡ @   £ ¤ ') 0 ¨ '2 0 '4 5 Grinding through we find ¤¥ '  3 ' ¢¦ ' ¢¡ ¦§ ¤¥ % ¨ #§£ !$%   % ¨ #§£ % ¨ #¢  !$%¥£ !$%¥£ !$%¡  !$%¥£ % ¨ #   % ¨ #¤£ % ¨ #¢  !$%     ¦§¨¤¥ ') '2 '4 ¦§ © ¤¥ ') '2 '4 ¦§ Don’t be shocked to see a rotation matrix © : we are after all rotating one right-handed orthogonal coord system into another. So the result in spherical polars is £¢ ¤¥ ¢ !$%¥£ !$%¡  ') 0 !$%¥£ % ¨ #   '2 % ¨ #¤£ '4 ¢ § % ¨ #   0 ¢ % ¨ #   ') 0 !$%¡  '2 ¢ § !$%¥£ !$%¡  § ! %¥£ '2 0 §% ¨ #§£ % ¨ #¢  '4 '2 0 ¨ '4 which is exactly the result in Cartesians. Q2 Find the divergence of the vector field ¥ § where is a constant vector (i) using Cartesian coordinates and (ii) using Spherical Polar coordinates.
70 LECTURE 6. VECTOR OPERATOR IDENTITIES A2 (i) Using Cartesian coords: %©¨ ¥ ¤ ¢¤ ¡ 0 ¨ ¡ 0 ¡ ' ¡ ( 0 5 5 5 ¤ 5¢¤ ¡ 0 ¨ ¡ 0 ¡ ' ¡ ( 0 5 5 5 § 5 (ii) Using Spherical polars ¥ ¦ 3 '  3 0 ¦ ¦ ' ¢¦ 0 ¦ ¡ ' ¢¡ and our first task is to find ¦ 3 and so on. We can’t do this by inspection, and finding their values requires more work than you might think! Recall ¤¥ '  3 ' ¢¦ '  ¡ ¦§ ¤¥ % ¨ #§£ ! %   % ¨ #§£ % ¨ #¢  !$% £ !$%¥£ !$%¡  !$%¥£ % ¨ #   % ¨ #¤£ % ¨ #¢  !$%     ¦§ ¤¥ ') '2 '4 ¦§ © ¤¥ ') '2 '4 ¦§ Now the point is the same point in space whatever the coordinate system, so ¦ 3 '  3 0 ¦ ¦ ' ¢¦ 0 ¦ ¡ ' ¢¡ ¦ ( ') 0 ¦ 5 '2 0 ¦ 8 '4 and using the inner product ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ ¤¥ '  3 ' ¨¦ ' ¢¡ ¦§ ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ ¤¥ ') '2 '4 ¦§ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ © ¤¥ ') '2 '4 ¦§ ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ ¤¥ ') '2 '4 ¦§ ¡ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ © ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ ¡ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ © ¡ ¡ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ © ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ For our particular problem, ¦ ( § ( , etc, where ( is a constant, so now we can write down ¦ 3 § ¢ % ¨ #¤£ !$%¡  ( 0 % ¨ #¤£ % ¨ #   5 0 !$%¥£ 8 ¦ ¦ § ¢ !$%¥£ !$%   ( 0 ! %¥£ % ¨ #   5 % ¨ #§£ 8 ¦ ¡ § ¢ % ¨ #   ( 0 !$%¡  5
6.15. GRAD, ETC, IN SPHERICAL POLARS 71 Now all we need to do is to bash out %©¨ ¥ § ¡ ¢ § ¡ ¦ 3 § 0 §% ¨ #¤£ ¢ ¦ ¦ % ¨ #¤£ £ 0 § % ¨ #¤£ ¦ ¡   In glorious detail this is %©¨ ¥ ¢ % ¨ #§£ ! %¡  ( 0 % ¨ #¤£ % ¨ #   5 0 !$% £ 8 0 % ¨ #§£ $ !$% ¡ £ % ¨ # ¡ £ ¢ !$%   ( 0 % ¨ #¢  5 ¥ % ¨ # £ !$%¥£ 8 0 % ¨ #§£ ¢ !$%   ( % ¨ #   5 A bit more bashing and you’ll find %©¨ ¥ % ¨ #§£ !$%   ( 0 % ¨ #§£ % ¨ #¢  5 0 !$%¥£ 8 '  3 This is EXACTLY what you worked out before of course. Take home messages from these examples: All the trig was a bit tedious, but there are three important points!   Just as physical vectors are independent of their coordinate systems, so are differential operators.   Don’t forget about the vector geometry you did in the 1st year. Rotation matrices are useful!   Spherical polars were NOT a good coordinate system in which to think about this problem. Let the symmetry guide you. IDR October 21, 2003

More Related Content

PPTX
vcla
byKunj Patel
 
PPTX
PHYSICS CH2-ELECTROMAGNETIC WAVES-1.pptx
byuiet231
 
PDF
Maths CA 1 ppt _20231229_170005_0000.pdf
byIamRiju2
 
PDF
Vector Calculus.
byManmohan Dash
 
PDF
Mathematical Background in Physics.pdf
byGajananHarde
 
PPT
16_05.ppt
byShantanuGolande
 
PPTX
16_05gg.pptx
byAyushChatterjee5
 
PDF
vectorcalculusandlinearalgebra-150518103010-lva1-app6892 (1).pdf
byShantanuGolande
 
vcla
byKunj Patel
 
PHYSICS CH2-ELECTROMAGNETIC WAVES-1.pptx
byuiet231
 
Maths CA 1 ppt _20231229_170005_0000.pdf
byIamRiju2
 
Vector Calculus.
byManmohan Dash
 
Mathematical Background in Physics.pdf
byGajananHarde
 
16_05.ppt
byShantanuGolande
 
16_05gg.pptx
byAyushChatterjee5
 
vectorcalculusandlinearalgebra-150518103010-lva1-app6892 (1).pdf
byShantanuGolande
 

Similar to Graddivcurl1

PPTX
Divergence,curl,gradient
byKunj Patel
 
PPT
Lecture notes on MAT122_Lec12_curl and divergence.ppt
byOdunayoDamilolaOsofu
 
PPTX
vectorcalculusandlinearalgebra-150518103010-lva1-app6892.pptx
byShalabhMishra10
 
PDF
Fields Lec 2
bycairo university
 
PPT
5. lec5 curl of a vector
byshabdrang
 
PDF
Emfbook
byAyushi Jaiswal
 
PPT
curl and divergence1 in electrical eng.ppt
bySamanZebari1
 
PPTX
AWP(KEC603), UNIT-1.pptx Anteena and wave propagation
byYaroKeYari1
 
PPTX
2. Vector Algebra.pptx
byMehrija
 
PPT
Ancillary maths ii
bySwathiSundari
 
PDF
13 05-curl-and-divergence
byAbdelrahman Elshaer
 
PPTX
Vector calculus
bySanthanam Krishnan
 
PPTX
EE8391 EMT Unit I Vector Calculus
byKarthikeyanK816516
 
PDF
EMF.0.11.VectorCalculus-I.pdf
byrsrao8
 
PDF
Vector-Calculus-Understanding-the-Mathematics-of-Fields-and-Flows.pdf
bykumaranmolgupta105
 
DOC
Notes notes vector calculus made at home (wecompress.com)
byAshish Raje
 
PPTX
Vector calculus 1st 2
byHIMANSHU DIWAKAR
 
PPTX
Vector calculus
bysujathavvv
 
PDF
Lec 02 2015 electromagnetic
byMagdi Saadawi
 
PDF
EMI_Chapter3_p2.pdf
byMagedAldhaeebi
 
Divergence,curl,gradient
byKunj Patel
 
Lecture notes on MAT122_Lec12_curl and divergence.ppt
byOdunayoDamilolaOsofu
 
vectorcalculusandlinearalgebra-150518103010-lva1-app6892.pptx
byShalabhMishra10
 
Fields Lec 2
bycairo university
 
5. lec5 curl of a vector
byshabdrang
 
Emfbook
byAyushi Jaiswal
 
curl and divergence1 in electrical eng.ppt
bySamanZebari1
 
AWP(KEC603), UNIT-1.pptx Anteena and wave propagation
byYaroKeYari1
 
2. Vector Algebra.pptx
byMehrija
 
Ancillary maths ii
bySwathiSundari
 
13 05-curl-and-divergence
byAbdelrahman Elshaer
 
Vector calculus
bySanthanam Krishnan
 
EE8391 EMT Unit I Vector Calculus
byKarthikeyanK816516
 
EMF.0.11.VectorCalculus-I.pdf
byrsrao8
 
Vector-Calculus-Understanding-the-Mathematics-of-Fields-and-Flows.pdf
bykumaranmolgupta105
 
Notes notes vector calculus made at home (wecompress.com)
byAshish Raje
 
Vector calculus 1st 2
byHIMANSHU DIWAKAR
 
Vector calculus
bysujathavvv
 
Lec 02 2015 electromagnetic
byMagdi Saadawi
 
EMI_Chapter3_p2.pdf
byMagedAldhaeebi
 

More from GHSKassKoronaMardan

PDF
5 2020 05_06!01_10_30_pm
byGHSKassKoronaMardan
 
PDF
5 2020 04_06!09_40_10_pm
byGHSKassKoronaMardan
 
PDF
Lmaac transmissionand distribution
byGHSKassKoronaMardan
 
PDF
Emf unit i
byGHSKassKoronaMardan
 
PDF
Corona1 150423103048-conversion-gate02
byGHSKassKoronaMardan
 
PDF
Corona topic
byGHSKassKoronaMardan
 
PDF
Armature reaction
byGHSKassKoronaMardan
 
PDF
Inductance and capacitance
byGHSKassKoronaMardan
 
DOC
Https _www.suit.edu.pk_uploads_past_papers_switchgear_protective_devices_-_b...
byGHSKassKoronaMardan
 
DOC
Https _www.suit.edu.pk_uploads_past_papers_power_transmission_distribution_-...
byGHSKassKoronaMardan
 
DOC
Https _www.suit.edu.pk_uploads_past_papers_power_transmission_distribution_-...
byGHSKassKoronaMardan
 
DOC
Https _www.suit.edu.pk_uploads_past_papers_power_transmission_distribution_-...
byGHSKassKoronaMardan
 
DOC
Https _www.suit.edu.pk_uploads_past_papers_electromagnetic_field_theory_-_ee315
byGHSKassKoronaMardan
 
DOC
Https _www.suit.edu.pk_uploads_past_papers_electric_machines_-_ii_-_elc315
byGHSKassKoronaMardan
 
5 2020 05_06!01_10_30_pm
byGHSKassKoronaMardan
 
5 2020 04_06!09_40_10_pm
byGHSKassKoronaMardan
 
Lmaac transmissionand distribution
byGHSKassKoronaMardan
 
Emf unit i
byGHSKassKoronaMardan
 
Corona1 150423103048-conversion-gate02
byGHSKassKoronaMardan
 
Corona topic
byGHSKassKoronaMardan
 
Armature reaction
byGHSKassKoronaMardan
 
Inductance and capacitance
byGHSKassKoronaMardan
 
Https _www.suit.edu.pk_uploads_past_papers_switchgear_protective_devices_-_b...
byGHSKassKoronaMardan
 
Https _www.suit.edu.pk_uploads_past_papers_power_transmission_distribution_-...
byGHSKassKoronaMardan
 
Https _www.suit.edu.pk_uploads_past_papers_power_transmission_distribution_-...
byGHSKassKoronaMardan
 
Https _www.suit.edu.pk_uploads_past_papers_power_transmission_distribution_-...
byGHSKassKoronaMardan
 
Https _www.suit.edu.pk_uploads_past_papers_electromagnetic_field_theory_-_ee315
byGHSKassKoronaMardan
 
Https _www.suit.edu.pk_uploads_past_papers_electric_machines_-_ii_-_elc315
byGHSKassKoronaMardan
 

Recently uploaded

PPTX
Optimizing Plant Maintenance — Key Elements of a Successful Maintenance Plan ...
byMaintWiz Technologies Private Limited
 
PPTX
TPM Metrics & Measurement: Drive Performance Excellence with TPM | MaintWiz
byMaintWiz Technologies Private Limited
 
PPTX
Natural Gas fundamentals and GRU for associated gas trap.pptx
byengineerhassan
 
PPTX
علي نفط.pptx هندسة النفط هندسة النفط والغاز
byengpe23e27
 
PDF
IPEC Presentation - Partial discharge Pro .pdf
bywaely1983
 
PDF
Structural Conservation Appraisal of Indian Monuments Preserving India’s Arch...
byAman Kumar Singh
 
PPTX
Industrial Plant Safety – Comprehensive Guide for Workplace Safety & Risk Pre...
byMaintWiz Technologies Private Limited
 
PPTX
Assessment 4 SRS Presentation - Final (2).pptx
byayush445302
 
PDF
Handheld_Laser_Welding_Presentation 2.pdf
bysinezioveluz
 
PPTX
The Importance of Maintenance Budgets — Maximize Reliability & Control Costs ...
byMaintWiz Technologies Private Limited
 
PPTX
Takt Time vs Cycle Time vs Lead Time.pptx
byE Concepts
 
PPTX
Optimizing Operations: Key Elements of a Successful Plant Maintenance Plan — ...
byMaintWiz Technologies Private Limited
 
PPTX
Preventive Maintenance Program for Compressors – Complete Guide
byMaintWiz Technologies Private Limited
 
PDF
Best Architecture in Kovilpatti - Amar Dexign Scape.pdf
byAmar Dexign scape
 
PPTX
Presentation on Purdue model for control hierarchy
bysamplayz126
 
PPTX
The Complete Guide to Energy Audits_ Unlocking Savings, Sustainability, and P...
bygreentechnexus2024
 
PPTX
Introduction Blockchains and Smart Contracts
bybobinson
 
PPTX
firewall Selection in production life pptx
byssuserb1479b
 
PPTX
UnrealGameplayAbilitySystemPresentation.pptx
byBenHowenstein
 
PPTX
Step-by-step guide to designing standard a microbiology laboratory in pharmac...
byshawkyabdo1
 
Optimizing Plant Maintenance — Key Elements of a Successful Maintenance Plan ...
byMaintWiz Technologies Private Limited
 
TPM Metrics & Measurement: Drive Performance Excellence with TPM | MaintWiz
byMaintWiz Technologies Private Limited
 
Natural Gas fundamentals and GRU for associated gas trap.pptx
byengineerhassan
 
علي نفط.pptx هندسة النفط هندسة النفط والغاز
byengpe23e27
 
IPEC Presentation - Partial discharge Pro .pdf
bywaely1983
 
Structural Conservation Appraisal of Indian Monuments Preserving India’s Arch...
byAman Kumar Singh
 
Industrial Plant Safety – Comprehensive Guide for Workplace Safety & Risk Pre...
byMaintWiz Technologies Private Limited
 
Assessment 4 SRS Presentation - Final (2).pptx
byayush445302
 
Handheld_Laser_Welding_Presentation 2.pdf
bysinezioveluz
 
The Importance of Maintenance Budgets — Maximize Reliability & Control Costs ...
byMaintWiz Technologies Private Limited
 
Takt Time vs Cycle Time vs Lead Time.pptx
byE Concepts
 
Optimizing Operations: Key Elements of a Successful Plant Maintenance Plan — ...
byMaintWiz Technologies Private Limited
 
Preventive Maintenance Program for Compressors – Complete Guide
byMaintWiz Technologies Private Limited
 
Best Architecture in Kovilpatti - Amar Dexign Scape.pdf
byAmar Dexign scape
 
Presentation on Purdue model for control hierarchy
bysamplayz126
 
The Complete Guide to Energy Audits_ Unlocking Savings, Sustainability, and P...
bygreentechnexus2024
 
Introduction Blockchains and Smart Contracts
bybobinson
 
firewall Selection in production life pptx
byssuserb1479b
 
UnrealGameplayAbilitySystemPresentation.pptx
byBenHowenstein
 
Step-by-step guide to designing standard a microbiology laboratory in pharmac...
byshawkyabdo1
 

Graddivcurl1

  • 1.
    Lecture 5 Vector Operators:Grad, Div and Curl In the first lecture of the second part of this course we move more to consider properties of fields. We introduce three field operators which reveal interesting collective field properties, viz.   the gradient of a scalar field,   the divergence of a vector field, and   the curl of a vector field. There are two points to get over about each:   The mechanics of taking the grad, div or curl, for which you will need to brush up your multivariate calculus.   The underlying physical meaning — that is, why they are worth bothering about. In Lecture 6 we will look at combining these vector operators. 5.1 The gradient of a scalar field Recall the discussion of temperature distribution throughout a room in the overview, where we wondered how a scalar would vary as we moved off in an arbitrary direction. Here we find out how to. If ¡£¢¥¤§¦©¨¦ is a scalar field, ie a scalar function of position ¤§¦©¨¦ in 3 dimensions, then its gradient at any point is defined in Cartesian co-ordinates by !#©$ % ¡ ¡ ¤(')10 ¡ ¨1'230 ¡ '465 It is usual to define the vector operator 7 ') ¤ 0 '2 ¨ 0 '4 which is called “del” or “nabla”. Then !#©$ % ¡98@7A¡ 51
  • 2.
    52 LECTURE 5.VECTOR OPERATORS: GRAD, DIV AND CURL Note immediately that 7A¡ is a vector field! Without thinking too carefully about it, we can see that the gradient tends to point in the direction of greatest change of the scalar field. Later we will be more precise.   Worked examples of gradient evaluation 1. ¡ ¤¢¡ Only ¤£ ¤ exists so 7A¡ ¦¥ ¤ ') 5 2. ¡ ¨§ ¡ § ¡ ¤¢¡ 0 ¨©¡ 0 ¡ , so 7A¡ ¥ ¤ ') 0 ¥ ¨ '2 0 ¥ '4 ¥ 5 3. ¡ , where is constant. 7A¡ ') ¤ 0 '2 ¨ 0 '4 ¢! ¤ 0 ¡ ¨ 0 # ! ') 0 ¡ '2 0 $ '4 ¨ 5 4. ¡ ¦% ¢ § ¡ % ¢¤ §¦©¨¦ ¦% ¢ § ¢¤ §¦©¨¦ Now #' )( 102' 043 )3 $( , #' )5 106' 073 )3 )5 , and #' $8 902' 043 )3 #8 , so 7A¡ % ¤ ') 0 % ¨ '2 0 % '4 A@ % @ §CB § ¤ ') 0 § ¨ '2 0 § '4ED But § GF ¤ ¡ 0 ¨ ¡ 0 ¡ , so § £ ¤ ¤ £ § and similarly for ¨ ¦ . Hence 7A¡ @ % @ §HB § ¤ ') 0 § ¨ '2 0 § '4 D @ % @ §PI ¤ ') 0 ¨ '2 0 '4 § Q @ % @ §SR §¤T 5
  • 3.
    5.2. THE SIGNIFICANCEOF GRAD 53 grad  ¡£¢¥¤¦¡¨§  © ¡¢¤¦¡ ¡¦§  © ¡ ¤¦¡ Figure 5.1: The directional derivative 5.2 The significance of grad We have seen that 7A¡ ¡ ¤ ') 0 ¡ ¨ '2 0 ¡ '4 so if we move a small amount @ @ ¤ ') 0 @ ¨ '2 0 @ '4 the change in ¡ is (see figure 5.1) @ ¡ ¡ ¤ @ ¤ 0 ¡ ¨ @ ¨ 0 ¡ @ 7A¡ @ 5 Now divide by @ @ ¡ @ 7 ¡ @ @ 5 But remember that @ @ , so @ £ @ is a unit vector in the direction of @ . So   !#©$ % ¡ has the property that the rate of change of ¡ wrt distance in a particular direction ( ' ) is the projection of !# $ % ¡ onto that direction (or the component of ! ©$ % ¡ in that direction). The quantity @ ¡ £ @ is called a directional derivative. Note that in general it has a different value for each direction, and so has no meaning until you specify the direction. We could also say that   At any point P, !#©$ % ¡ points in the direction of greatest change of ¡ at P, and has magnitude equal to the rate of change of ¡ wrt distance in that direction. Another nice property emerges if we think of a surface of constant ¡ – that is the locus ¢¤ §¦©¨¦ for ¡£¢¥¤§¦©¨¦ !$#%' $ #(
  • 4.
    54 LECTURE 5.VECTOR OPERATORS: GRAD, DIV AND CURL −4 −2 0 2 4 −4 −2 0 2 4 0 0.02 0.04 0.06 0.08 0.1 Figure 5.2: If we move a tiny amount within the surface, that is in any tangential direction, there is no change in ¡ , so @ ¡ £ @ ¡  . So for any @ £ @ in the surface 7A¡ @ @   5 This can only be satisfied if   ! ©$ % ¡ is NORMAL to a surface of constant ¡ . Surface of constant U gradU Surface of constant U These are called Level Surfaces Figure 5.3: 5.3 The divergence of a vector field The divergence computes a scalar quantity from a vector field by differentiation.
  • 5.
    5.4. THE SIGNIFICANCEOF  ¢¡¤£ 55 More precisely, if ¥ ¢¥¤§¦©¨¦ is a vector function of position in 3 dimensions, that is ¥ §¦ ')0 ¦ ¡ '2 0 ¦ '4 , then its divergence at any point is defined in Cartesian co-ordinates by %©¨ ¥ ¦ ¤ 0 ¦ ¡ ¨ 0 ¦ We can write this in a simplified notation using a scalar product with the 7 vector differential operator: %©¨ ¥ ') ¤ 0 '2 ¨ 0 '4 ¥ 7 ¥ Notice that the divergence of a vector field is a scalar field.   Worked examples of divergence evaluation ¥ div¥¤ ') ¢ ¤ ') 0 ¨ '2 0 '4 3   § ¢ £ § where is constant Let us show the third example. The ¤ component of £ § is ¤ 5¢ ¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ , and we need to find £ ¤ of it. ¤ ¤ 5¢ ¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ 5¢ ¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ 0 ¤! ¥ ¢¥¤ ¡ 0 ¨ ¡ 0 ¡ # ¡ 5¥ ¤ § %$ ¤ ¡ § ¡ Adding this to similar terms for ¨ and gives § $ ¢¤ ¡ 0 ¨ ¡ 0 ¡ § ¡ § ¢' # ¡  5.4 The significance of (0)21 Consider a typical vector field, water flow, and denote it by ¥ ¢ . This vector has magnitude equal to the mass of water crossing a unit area perpendicular to the direction of ¥ per unit time. Now take an infinitesimal volume element @#3 and figure out the balance of the flow of ¥ in and out of @43 . To be specific, consider the volume element @43 @ ¤ @ ¨ @ in Cartesian co-ordinates, and think first about the face of area @ ¤ @ perpendicular to the ¨ axis and facing outwards in the negative ¨ direction. (That is, the one with surface area @65 @ ¤ @ '2 .) The component of the vector ¥ normal to this face is ¥ '2 7¦ 5 , and is pointing inwards, and so the its contribution to the OUTWARD flux from this surface is ¥ @©5 ¦ 5 ¢ ¨ @ @ ¤ 5 (Flux here means mass per unit time.)
  • 6.
    56 LECTURE 5.VECTOR OPERATORS: GRAD, DIV AND CURL dS = -dxdz j y x z dz dx dy jdS = +dxdz Figure 5.4: Elemental volume for calculating divergence. A similar contribution, but of opposite sign, will arise from the opposite face, but we must remember that we have moved along ¨ by an amount @ ¨ , so that this OUTWARD amount is ¦ 5 ¢¨ 0 @ ¨ @ @ ¤ ¦ 5 0 ¦ 5 ¨ @ ¨ @ ¤ @ The total outward amount from these two faces is ¦ 5 ¨ @ ¨ @ ¤ @ ¦ 5 ¨ @#3 Summing the other faces gives a total outward flux of ¦ ( ¤ 0 ¦ 5 ¨ 0 ¦ 8 @#3 7 ¥ @#3 Take home message: The divergence of a vector field represents the flux generation per unit volume at each point of the field. (Divergence because it is an efflux not an influx.) Interestingly we also saw that the total efflux from the infinitesimal volume was equal to the flux inte- grated over the surface of the volume. (NB: The above does not constitute a rigorous proof of the assertion because we have not proved that the quantity calculated is independent of the co-ordinate system used, but it will suffice for our purposes. 5.5 The Laplacian: (0)21 ¡£¢¥¤§¦ (©¨ of a scalar field Recall that !# $ % ¡ of any scalar field ¡ is a vector field. Recall also that we can compute the divergence of any vector field. So we can certainly compute %©¨ ¢ ! ©$ % ¡ , even if we don’t know what it means yet.
  • 7.
    5.5. THE LAPLACIAN: ¢¡¤£ ¢¡ £¢¥¤   ¡ OF A SCALAR FIELD 57 Here is where the 7 operator starts to be really handy. 7 ¢ 7 ¡ ') ¤ 0 '2 ¨ 0 '4 ') ¤ 0 '2 ¨ 0 '4 ¡ ') ¤ 0 '2 ¨ 0 '4 ') ¤ 0 '2 ¨ 0 '4 ¡ ¡ ¤ ¡ 0 ¡ ¨ ¡ 0 ¡ ¡ ¡ ¡ ¡ ¤ ¡ 0 ¡ ¡ ¨ ¡ 0 ¡ ¡ ¡ This last expression occurs frequently in engineering science (you will meet it next in solving Laplace’s Equation in partial differential equations). For this reason, the operator ¦ ¡ is called the “Laplacian” ¦ ¡ ¡ ¡ ¤ ¡ 0 ¡ ¨ ¡ 0 ¡ ¡ ¡ Laplace’s equation itself is ¦ ¡ ¡     Examples of §©¨ evaluation § ¨ ¨¨!#$¨%'(¨0) 1 ¨ 32 456327'1(8 ¨ 9A@ B Let’s prove the last example (which is particularly significant – can you guess why?). £ § ¢¥¤¢¡ 0 ¨©¡ 0 ¡ ' ¡ and so ¤ ¤ ¢¥¤ ¡ 0 ¨ ¡ 0 ¡ ' ¡ ¤ ¤ 5¢¤ ¡ 0 ¨ ¡ 0 ¡ ¡ ¢¥¤ ¡ 0 ¨ ¡ 0 ¡ ¡ 0 ¤ 5¤ 5¢¤ ¡ 0 ¨ ¡ 0 ¡ # ¡ ¢ £ § ¢ 0 ¤ ¡ £ § ¡ Adding up similar terms for ¨ and ¦ ¡ § § 0 ¢¥¤¢¡ 0 ¨ ¡ 0 ¤¢¡ § ¡  
  • 8.
    58 LECTURE 5.VECTOR OPERATORS: GRAD, DIV AND CURL 5.6 The curl of a vector field So far we have seen the operator 7   Applied to a scalar field 7 ¡ ; and   Dotted with a vector field 7 ¥ . You are now overwhelmed by that irrestible temptation to   cross it with a vector field 7   ¥ This gives the curl of a vector field 7¡  ¥ 8 £¢ ¥¤¢ ¥ We can follow the pseudo-determinant recipe for vector products, so that 7¡  ¥ ¦¦¦¦¦¦ ') '2 '4 )( )5 $8¦ ( ¦ 5 ¦ 8 ¦¦¦¦¦¦ ¦ 8 ¨ ¦ 5 ') 0 ¦ ( ¦ 8 ¨ '2 0 ¦ 5 ¤ ¦ ( ¨ '4   Examples of curl evaluation ¥ 7§  ¥ ¨ ') 0 ¤ '2 ¥ '4 ¤¢¡¨©¡ '4 ¥ ¤¢¡¨ ') ¥ ¤ ¨©¡ '2 5.7 The signficance of curl Perhaps the first example gives a clue. The field ¥ ¨ ') 0 ¤ '2 is sketched in Figure 5.5(a). (It is the field you would calculate as the velocity field of an object rotating with ¨   ¦   ¦ .) This field has a curl of ¥ '4 , which is in the r-h screw out of the page. You can also see that a field like this must give a finite value to the line integral around the complete loop © ¥ @ 5 In fact curl is closely related to the line integral around a loop. The circulation of a vector ¥ round any closed curve is defined to be ¥ @ and the curl of the vector field ¥ represents the vorticity, or circulation per unit area, of the field. Our proof uses the small rectangular element @ ¤ by @ ¨ shown in Figure 5.5(b). Consider the circulation round the perimeter of a rectangular element.
  • 9.
    5.8. SOME DEFINITIONSINVOLVING DIV, CURL AND GRAD 59 y x ax(y) a(x)y ax(y+dy) ay(x+dx) dx dy y y x x+dx y+dy Figure 5.5: (a) A rough sketch of the vector field ¨ ') 0 ¤ '2 . (b) An element in which to calculate curl. The fields in the ¤ direction at the bottom and top are ¦ ( ¢ ¨ $ # % ¦ ( ¢¥¨ 0 @ ¨ ¦ ( ¢¥¨ 0 ¦ ( ¨ @ ¨ and the fields in the ¨ direction at the left and right are ¦ 5 ¢¤ $ # % ¦ 5 ¢¤ 0 @ ¤ §¦ 5 ¢¤ 0 ¦ 5 ¤ @ ¤ Starting at the bottom and working round in the anticlockwise sense, the four contributions to the circu- lation @ are therefore as follows, where the minus signs take account of the path being oppose to the field: @ 0 ¦ ( ¢ ¨ @ ¤ 0 ¦ 5 ¢¥¤ 0 @ ¤ @ ¨ ¦ ( ¢ ¨ 0 @ ¨ @ ¤ ¦ 5 ¢¤ @ ¨ 0 ¦ ( ¢ ¨ @ ¤ 0 B ¦ 5 ¢¤ 0 ¦ 5 ¤ @ ¤ @ ¨ D B ¦ ( ¢¥¨ 0 ¦ ( ¨ @ ¨ @ ¤ D ¦ 5 ¢¤ @ ¨ ¦ 5 ¤ ¦ ( ¨ @ ¤ @ ¨ ¢ 7§  ¥ @65 where @65 @ ¤ @ ¨ '4 . NB: Again, this is not a completely rigorous proof as we have not shown that the result is independent of the co-ordinate system used. 5.8 Some definitions involving div, curl and grad   A vector field with zero divergence is said to be solenoidal.   A vector field with zero curl is said to be irrotational.   A scalar field with zero gradient is said to be, er, well, constant. IDR October 21, 2003
  • 10.
    60 LECTURE 5.VECTOR OPERATORS: GRAD, DIV AND CURL
  • 11.
    Lecture 6 Vector OperatorIdentities In this lecture we look at more complicated identities involving vector operators. The main thing to appreciate it that the operators behave both as vectors and as differential operators, so that the usual rules of taking the derivative of, say, a product must be observed. We shall derive these using both conventional grunt, and using the compact notation. Note that the relevance of these identities may only become clear later in other Engineering courses. 6.1 Identity 1: curl grad ¨ =   ¡   ¨ ¢ £ 7§  7A¡ ¦¦¦¦¦¦ ') '2 '4 ¤£ ¤ ¤£ ¨ ¤£ ¡ £ ¤ ¡ £ ¨ ¡ £ ¦¦¦¦¦¦ ') ¡ ¡ ¨ ¡ ¡ ¨ 0 '2 ¢ 0 '4 ¢ ¤ 5 Note that 7¡  7 can be thought of as a null operator. 6.2 Identity 2: div curl ¥ =   ¦§  ¡ ¥¨¢ © 7 7§  ¥ ¦¦¦¦¦¦ £ ¤ ¤£ ¨ ¤£ £ ¤ ¤£ ¨ ¤£ ¦ ( ¦ 5 ¦ 8 ¦¦¦¦¦¦ ¡ ¦ 8 ¤ ¨ ¡ ¦ 5 ¤ ¡ ¦ 8 ¨ ¤ 0 ¡ ¦ ( ¨ ¡ ¦ 5 ¤ ¡ ¦ ( ¨   61
  • 12.
    62 LECTURE 6.VECTOR OPERATOR IDENTITIES 6.3 Identity 3: div and curl of ¨ ¥ Suppose that ¡£¢ is a scalar field and that ¥ ¢ is a vector field and we are interested in the product ¡ ¥ , which is a vector field so we can compute its divergence and curl. For example the density ¡ ¢ of a fluid is a scalar field, and the instantaneous velocity of the fluid ¢ ¢ is a vector field, and we are probably interested in mass flow rates for which we will be interested in ¡ ¢ ¢ ¢ . The divergence (a scalar) of the product ¡ ¥ is given by: 7 ¢ ¡ ¥ 7 ¢ ¡ ¥ ¡£¢ 7 ¥ 0 ¢ 7 ¡ ¥ ¡ %©¨ ¥ 0 ¢ !#©$ % ¡ ¥ In a similar way, we can take the curl of the vector field ¡ ¥ , and the result should be a vector field: 7¡  ¢ ¡ ¥ ¡ 7§  ¥ 0 ¢ 7A¡   ¥ 5 6.4 Identity 4: div of ¥ ¡ £ Life quickly gets trickier when vector or scalar products are involved: For example, it is not that obvious that %6¨ ¢ ¥  ¥¤ £¢ ¥¤¥ ¤ ¥ £¢ ¥¤¤ To show this, use the determinant: ¦¦¦¦¦¦ £ ¤§¦ £ ¤©¨ ¤£ ¤ ¦ ( ¦ 5 ¦ 8 ( 5 8 ¦¦¦¦¦¦ ¤ ¦ 5 8 ¦ 8 5 0 ¨ ¦ 8 ( ¦ ( 8 0 ¦ ( 5 ¦ 5 ( 5 5 5 $ % ! ¢ ! % ¢% 5 5 5 £¢ ¥¤¥ ¤ ¥ ¢ curl ¤ 6.5 Vector operator identities in HLT There is a kind of cottage industry in inventing vector identities. HLT contains a lot of them. So why not leave it at that? First, since !#©$ % , %©¨ and ¢ ¤ describe key aspects of vectors fields, they arise often in practice, and so the identities can save you a lot of time and hacking of partial derivatives, as we will see when we consider Maxwell’s equation as an example later. Secondly, they help to identify other practically important vector operators. We now look at such an example.
  • 13.
    6.6. IDENTITY 5: ¢¡ ¢¤£ ¢¦¥  ¨§ 63 6.6 Identity 5: © ¤ ¡ ¥ ¡ £ £¢ ¥¤¢ ¥  ¥¤ ¦¦¦¦¦¦ ') '2 '4 ¤£ ¤ £ ¨ ¤£ ¦ 5 8 ¦ 8 5 ¦ 8 ( ¦ ( 8 ¦ ( 5 ¦ 5 ( ¦¦¦¦¦¦ so the ') component is ¨ ¢ ¦ ( 5 ¦ 5 ( ¢ ¦ 8 ( ¦ ( 8 which can be written as the sum of four terms: ¦ ( 5 ¨ 0 8 D ( ¦ 5 ¨ 0 ¦ 8 D 0 5 ¨ 0 8 ¦ ( ¦ 5 ¨ 0 ¦ 8 ( Adding ¦ ( )( to the first of these, and subtracting from the last, and doing the same with ( )( to the other two terms, we find that: 7§  ¢ ¥   ¤ ¢ 7 ¤ ¥ ¢ 7 ¥ ¤ 0 ¤ 76 ¥ ¥ 7 ¤ where ¥ 76 can be regarded as new, and very useful, scalar differential operator. 6.7 Definition of the operator ¥ ¦§  ! This is a scalar operator, but it can obviously can be applied to a scalar field, resulting in a scalar field, or to a vector field resulting in a vector field: ¥ 7 8 B ¦ ( ¤ 0 ¦ 5 ¨ 0 ¦ 8 D 5 6.8 Identity 6: © ¤ ¡ © ¤ ¥ for you to derive The following important identity is stated, and let as an exercise: £¢ ¥¤¢ £¢ ¥¤¥ ! ©$ % %©¨ ¥ ¦ ¡ ¥ where ¦ ¡ ¥ ¦ ¡ ¦ ( ') 0 ¦ ¡ ¦ 5 '2 0 ¦ ¡ ¦ 8 '4   Example of Identity 6: electromagnetic waves Background: Maxwell established a set of four vector equations which are fundamental to working out how eletromagnetic waves propagate. The entire telecommunications industry is built on these! %©¨$# ¡ %©¨ §   £¢ ¤% (' § £¢ ¥¤0) 1 0 (' #
  • 14.
    64 LECTURE 6.VECTOR OPERATOR IDENTITIES In addition, we can assume the following § ¡  3  £¢ ) , 1 ¥¤ % , # ¡¦ 3 ¦§¢ % , where all the scalars are constants. Question: Show that in a material with no free charge, ¡   , and with zero conductivity, ¤   , the eletric field % must be a solution of the wave equation ¦ ¡ % ¡  3  £¢¨¦ 3 ¦§¢ ¢ ¡ % £ (' ¡ 5 Answer: The good news is that we can do this knowing little about EM waves! %6¨$# %©¨ ¢ ¦ 3 ¦§¢ % ©¦ 3 ¦¢ %©¨ % ¡  %©¨ § %©¨ ¢   3  £¢ ) ¥  3  £¢ %6¨$)   £¢ ¥¤% § £ ('   3  £¢ ¢ ) £ (' ¢ ¤) 1 0 # £ (' ¤ 0 ¦ 3 ¦§¢ ¢ % £ (' But we know (or rather you worked out) that £¢ ¤£¢ ¥¤0% !# $ % %©¨ $% ¦ ¡ % , so ¢ ¤£¢ ¤0% ¢ ¤   3  ¢ ¢ ) £ (' !#©$ % %©¨ (% ¦ ¡ % so interchanging the order of partial differentation, and using %©¨ $%   :   3  £¢ (' ¢ ¤0) ¦ ¡ %   3  £¢ (' B ¦ 3 ¦§¢ % (' D ¦ ¡ %   3  £¢¨¦ 3 ¦§¢ ¡ % (' ¡ ¦ ¡ % 6.9 Grad, div, curl and ¥ in curvilinear co-ordinate systems It is possible to obtain general expressions for grad, div and curl in any orthogonal curvilinear co-ordinate system by making use of the factors which were introduced in Lecture 4. We recall that the unit vector in the direction of increasing , with and being kept constant, is where is the radius vector, and ¦¦¦¦ ¦¦¦¦ and similar expressions apply for the other co-ordinate directions. Then @ © @ 0 ! ¢ @ 0 # @ 5
  • 15.
    6.10. GRAD INCURVILINEAR COORDINATES 65 6.10 Grad in curvilinear coordinates Using the properties of the gradient of a scalar field obtained previously, 7A¡ @ @ ¡ ¡ @ 0 ¡ @ 0 ¡ @ It follows that 7A¡ ¢ @ 0 ! ¢ @ 0 # @ ¡ @ 0 ¡ @ 0 ¡ @ The only way this can be satisfied for independent @ , @ , @ is when 7A¡ ¡ ' 0 ! ¡ '¢ 0 ¡ '# 6.11 Divergence in curvilinear coordinates Expressions can be obtained for the divergence of a vector field in orthogonal curvilinear co-ordinates by making use of the flux property. We consider an element of volume @#3 . Although earlier we derived this as the volume of a parallelop- iped, and found that the @#3 ¦¦¦¦ ¢¥¤§¦©¨¦ ¢ ¦ ¦ ¦¦¦¦ @ @ @ If the curvilinear coordinates are orthogonal then the little volume is a cuboid (to first order in small quantities) and @#3 ¡ ! @ @ @ 5 However, it is not quite a cuboid: the area of two opposite faces will differ as the scale parameters are functions of , and in general. So the net efflux from the two faces in the '¢ direction shown in Figure 6.1 is B ¦ ! 0 ¦ ! @ D B 0 @ D B 0 @ D @ @ ¦ ! @ @ ¢ ¦ ! @ @ @ which is easily shown by multiplying the first line out and dropping second order terms (i.e. ¢ @ $¡ ). By definition div is the net efflux per unit volume, so summing up the other faces: %©¨ ¥ @#3 ¢ ¦ ! 0 ¢ ¦ ! 0 ¢ ¦ ! @ @ @ ¡ %6¨ ¥ ! @ @ @ ¢ ¦ ! 0 ¢ ¦ ! 0 ¢ ¦ ! @ @ @
  • 16.
    66 LECTURE 6.VECTOR OPERATOR IDENTITIES w u y The scale params are h (v) dw h (v+dv) dw h (v+dv) du h (v) du u w w u h dvv functions of u,v,w Figure 6.1: Elemental volume for calculating divergence in orthogonal curvilinear coordinates So, finally, %6¨ ¥ ! ¢ ¦ ! 0 ¢ ¦ ! 0 ¢ ¦ ! 6.12 Curl in curvilinear coordinates Recall from Lecture 5 that we computed the component of curl as the circulation per unit area — the contents of the brackets ¢ in the expression for the element of circulation @ ¦ 5 ¤ ¦ ( ¨ @ ¤ @ ¨ By analogy with our derivation of divergence, you will realize that for an orthogonal curvilinear coordi- nate system we can write the area as ! @ @ . But the opposite sides are no longer quite of the same length. The lower of the pair in Figure 6.2 is length ¢ @ , but the upper is of length ¢ 0 @ @ Summing this pair gives a contribution to the circulation ¦ ¢ ¢ @ ¦ ¢ 0 @ ¢ 0 @ @ ¢ ¦ @ @ and together with the other pair: @ ¢ ¦ 0 ¢ ! ¦ ! @ @ So the circulation per unit area is @ ! @ @ ! ¢ ! ¦ ! ¢ ¦
  • 17.
    6.13. THE LAPLACIANIN CURVILINEAR COORDINATES 67 y y a a u u u+du u u u v+dv (v+dv) h (v+dv) du dv (v) h (v) du Figure 6.2: Elemental loop for calculating curl in orthogonal curvilinear coordinates and hence curl is £¢ ¥¤¥ ¢ ¦ ¦ ! ¢ ¦ ¢ ! ¦ ! ' 0 ¢ ¦ ¢ ¦ '¢ 0 ! ¢ ! ¦ ! ¢ ¦ '# 6.13 The Laplacian in curvilinear coordinates Substitution of the components of !#©$ % ¡ into the expression for %©¨ ¥ immediately (!*?) gives the following expression for the Laplacian in general orthogonal co-ordinates: ¦ ¡ ¡ ! B ! ¡ 0 ! ¡ 0 ! ¡ D 5 6.14 Grad, etc, in cylindrical polars We recall that § ! %¡  ') 0 §% ¨ #¢  '2 0 '4 , and that £ , and so F ¢ !$% ¡   0 ¤£¦¥ ¡   ¦ ¡ § ¢ § ¡ % ¨ # ¡   0 § ¡ ! % ¡   § ¦
  • 18.
    68 LECTURE 6.VECTOR OPERATOR IDENTITIES Hence ! ©$ % ¡ ¡ § '  3 0 § ¡   ' ¢¡ 0 ¡ '4 %©¨ ¥ § ¢ § ¦ 3 § 0 ¦ ¡   0 ¦ 8 £¢ ¥¤¥ § ¦ 8   ¦ ¡ '  3 0 ¦ 3 ¦ 8 § ' ¢¡ 0 § ¢ § ¦ ¡ § ¦ 3   '4 The derivation of the expression for ¦ ¡ ¡ in cylindrical polar co-ordinates is set as a tutorial exercise. 6.15 Grad, etc, in spherical polars We recall that ¨§% ¨ #¤£ !$%¡  ') 0 § % ¨ #¤£ % ¨ #   '2 0 § !$%¥£ '4 so that § ¢ % ¨ # ¡ £ ¢ ! % ¡   0 % ¨ # ¡   0 !$% ¡ £ ¡ § ¢ § ¡ ! % ¡ £ ¢ !$% ¡   0 % ¨ # ¡   0 § ¡ % ¨ # ¡ £ § § ¢ § ¡ % ¨ # ¡ £ ¢ % ¨ # ¡   0 !$% ¡   ¨§ % ¨ #¤£ Hence ! ©$ % ¡ ¡ § '  3 0 § ¡ £ ' ¢¦ 0 § % ¨ #§£ ¡   ' ¨¡ %©¨ ¥ § ¡ ¢ § ¡ ¦ 3 § 0 § % ¨ #§£ ¢ ¦ ¦ % ¨ #§£ £ 0 § % ¨ #§£ ¦ ¡   £¢ ¥¤¥ '  3 § % ¨ #§£ £ ¢ ¦ ¡ % ¨ #§£   ¢ ¦ ¦ 0 ' ¢¦ §% ¨ #¤£   ¢ ¦ 3 § ¢ ¦ ¡ § % ¨ #¤£ 0 ' ¢¡ § § ¢ ¦ ¦ § £ ¢ ¦ 3   The derivation of the expression for ¦ ¡ ¡ is set as a tutorial exercise.   Examples Q1 Find ¢ ¤¥ in (i) Cartesians and (ii) Spherical poplars when ¥ ¤ ¢¥¤ ') 0 ¨ '2 0 '4 .
  • 19.
    6.15. GRAD, ETC,IN SPHERICAL POLARS 69 A1 (i) In Cartesians, using the pseudo determinant gives ¢ ¤¥ '2 0 ¨ '4 . (ii) By inspection, in spherical polars ¥ § % ¨ #¤£ ! %¡  ¢ § '  3 so ¦ 3 ¨§ ¡ % ¨ #¤£ !$%¡ ¡  ¦ ¦ ¡ ¢  ¦ ¡   5 Hence £¢ ¤¥ ' ¨¦ §% ¨ #¤£   ¢ § ¡ % ¨ #¤£ !$%¡  0 ' ¢¡ § £ ¢ § ¡ % ¨ #§£ !$%   ' ¨¦ §% ¨ #¤£ ¢ § ¡ % ¨ #§£ % ¨ #   0 ' ¢¡ § $ § ¡ !$% £ !$%   ' ¢¦ ¢ §% ¨ #¢  0 ' ¢¡ ¢ § !$%¥£ !$%¡  Now, these two results should be the same, but to check we need expressions for '  3 etc in terms of ') etc. Remember that we can work out the unit vectors '  3 and so on in terms of ') etc using '  3 @ §   ' ¢¦ ¡ @ £   ' ¢¡ @   £ ¤ ') 0 ¨ '2 0 '4 5 Grinding through we find ¤¥ '  3 ' ¢¦ ' ¢¡ ¦§ ¤¥ % ¨ #§£ !$%   % ¨ #§£ % ¨ #¢  !$%¥£ !$%¥£ !$%¡  !$%¥£ % ¨ #   % ¨ #¤£ % ¨ #¢  !$%     ¦§¨¤¥ ') '2 '4 ¦§ © ¤¥ ') '2 '4 ¦§ Don’t be shocked to see a rotation matrix © : we are after all rotating one right-handed orthogonal coord system into another. So the result in spherical polars is £¢ ¤¥ ¢ !$%¥£ !$%¡  ') 0 !$%¥£ % ¨ #   '2 % ¨ #¤£ '4 ¢ § % ¨ #   0 ¢ % ¨ #   ') 0 !$%¡  '2 ¢ § !$%¥£ !$%¡  § ! %¥£ '2 0 §% ¨ #§£ % ¨ #¢  '4 '2 0 ¨ '4 which is exactly the result in Cartesians. Q2 Find the divergence of the vector field ¥ § where is a constant vector (i) using Cartesian coordinates and (ii) using Spherical Polar coordinates.
  • 20.
    70 LECTURE 6.VECTOR OPERATOR IDENTITIES A2 (i) Using Cartesian coords: %©¨ ¥ ¤ ¢¤ ¡ 0 ¨ ¡ 0 ¡ ' ¡ ( 0 5 5 5 ¤ 5¢¤ ¡ 0 ¨ ¡ 0 ¡ ' ¡ ( 0 5 5 5 § 5 (ii) Using Spherical polars ¥ ¦ 3 '  3 0 ¦ ¦ ' ¢¦ 0 ¦ ¡ ' ¢¡ and our first task is to find ¦ 3 and so on. We can’t do this by inspection, and finding their values requires more work than you might think! Recall ¤¥ '  3 ' ¢¦ '  ¡ ¦§ ¤¥ % ¨ #§£ ! %   % ¨ #§£ % ¨ #¢  !$% £ !$%¥£ !$%¡  !$%¥£ % ¨ #   % ¨ #¤£ % ¨ #¢  !$%     ¦§ ¤¥ ') '2 '4 ¦§ © ¤¥ ') '2 '4 ¦§ Now the point is the same point in space whatever the coordinate system, so ¦ 3 '  3 0 ¦ ¦ ' ¢¦ 0 ¦ ¡ ' ¢¡ ¦ ( ') 0 ¦ 5 '2 0 ¦ 8 '4 and using the inner product ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ ¤¥ '  3 ' ¨¦ ' ¢¡ ¦§ ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ ¤¥ ') '2 '4 ¦§ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ © ¤¥ ') '2 '4 ¦§ ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ ¤¥ ') '2 '4 ¦§ ¡ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ © ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ ¡ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ ¡ ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ ¡ © ¡ ¡ ¤¥ ¦ 3 ¦ ¦ ¦ ¡ ¦§ © ¤¥ ¦ ( ¦ 5 ¦ 8 ¦§ For our particular problem, ¦ ( § ( , etc, where ( is a constant, so now we can write down ¦ 3 § ¢ % ¨ #¤£ !$%¡  ( 0 % ¨ #¤£ % ¨ #   5 0 !$%¥£ 8 ¦ ¦ § ¢ !$%¥£ !$%   ( 0 ! %¥£ % ¨ #   5 % ¨ #§£ 8 ¦ ¡ § ¢ % ¨ #   ( 0 !$%¡  5
  • 21.
    6.15. GRAD, ETC,IN SPHERICAL POLARS 71 Now all we need to do is to bash out %©¨ ¥ § ¡ ¢ § ¡ ¦ 3 § 0 §% ¨ #¤£ ¢ ¦ ¦ % ¨ #¤£ £ 0 § % ¨ #¤£ ¦ ¡   In glorious detail this is %©¨ ¥ ¢ % ¨ #§£ ! %¡  ( 0 % ¨ #¤£ % ¨ #   5 0 !$% £ 8 0 % ¨ #§£ $ !$% ¡ £ % ¨ # ¡ £ ¢ !$%   ( 0 % ¨ #¢  5 ¥ % ¨ # £ !$%¥£ 8 0 % ¨ #§£ ¢ !$%   ( % ¨ #   5 A bit more bashing and you’ll find %©¨ ¥ % ¨ #§£ !$%   ( 0 % ¨ #§£ % ¨ #¢  5 0 !$%¥£ 8 '  3 This is EXACTLY what you worked out before of course. Take home messages from these examples: All the trig was a bit tedious, but there are three important points!   Just as physical vectors are independent of their coordinate systems, so are differential operators.   Don’t forget about the vector geometry you did in the 1st year. Rotation matrices are useful!   Spherical polars were NOT a good coordinate system in which to think about this problem. Let the symmetry guide you. IDR October 21, 2003