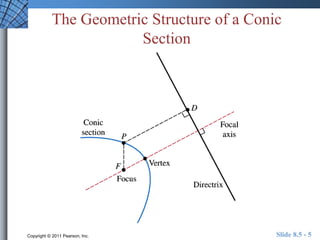
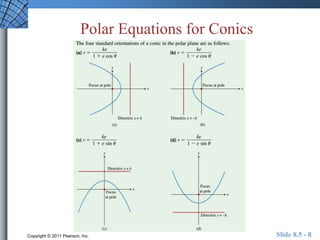
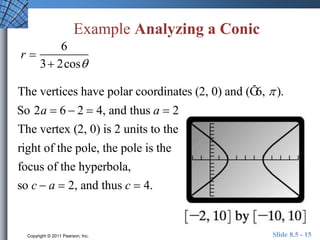
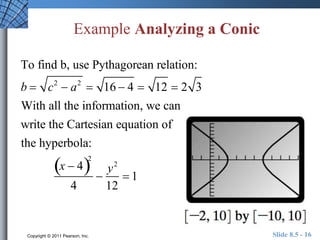
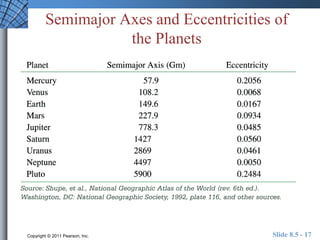
This document discusses polar equations of conics. It introduces the eccentricity and focus-directrix definition of conics. It explains how to write polar equations for conics given the eccentricity and directrix. Examples are provided of writing polar equations for conics and analyzing conics from their polar equations, including identifying the type of conic and determining values like the eccentricity. The document also briefly discusses the orbits of planets.