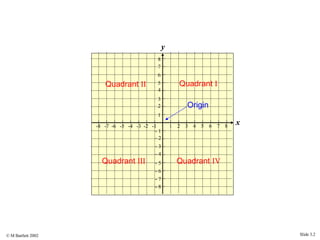
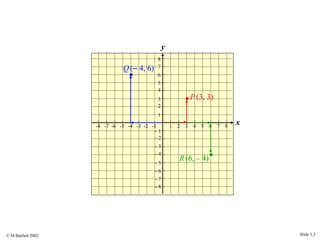
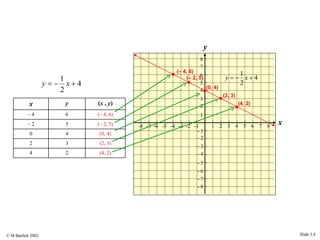
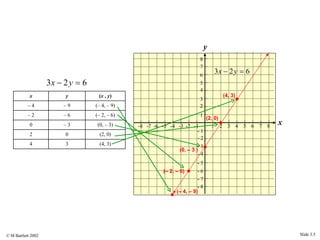
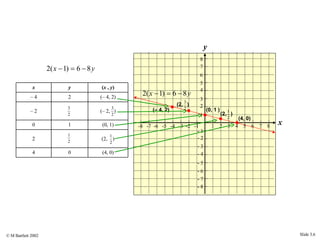
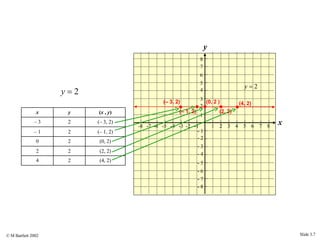
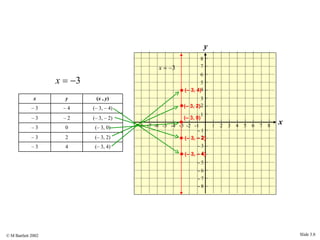
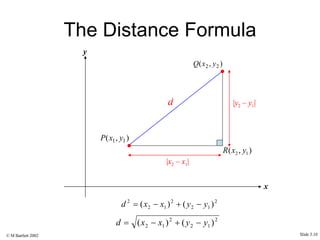
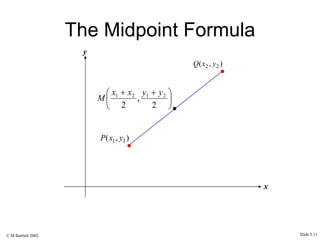
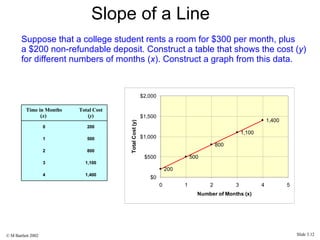
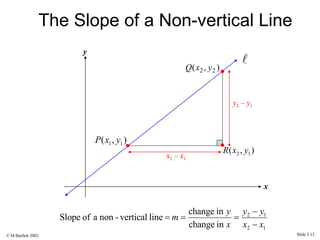
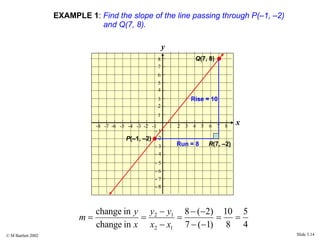
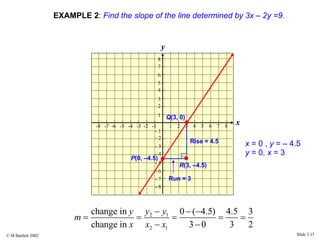
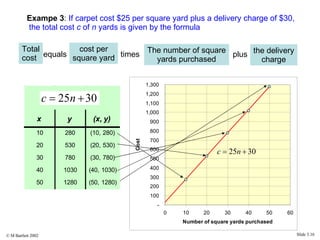
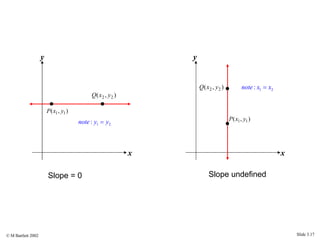
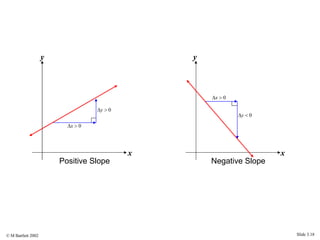
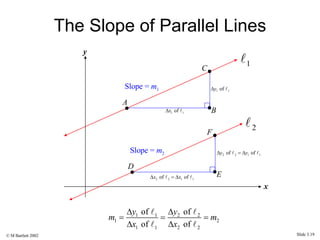
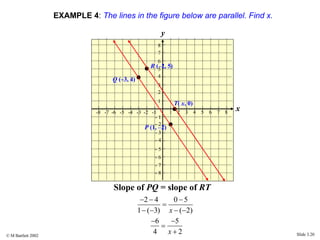
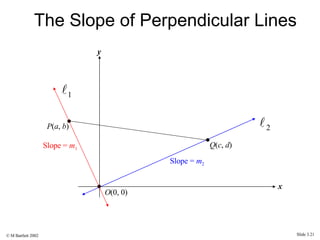
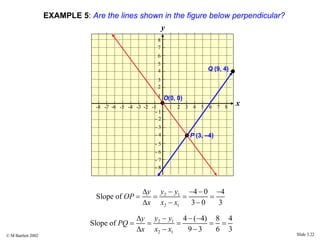
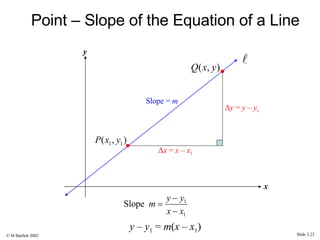
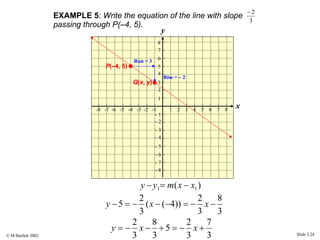
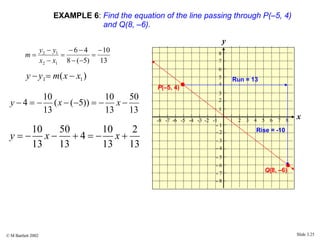
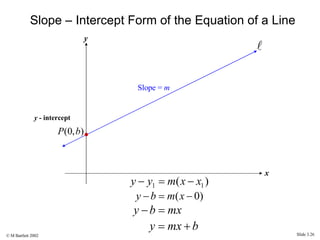
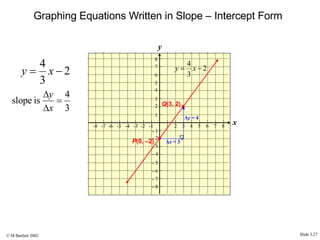
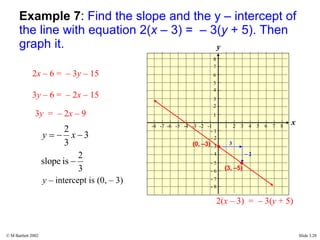
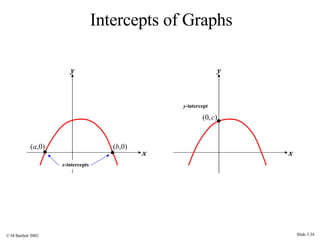
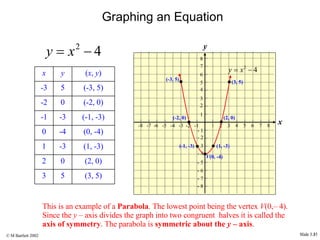
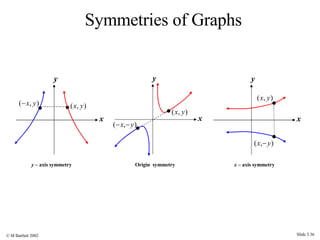
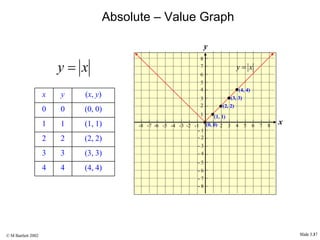
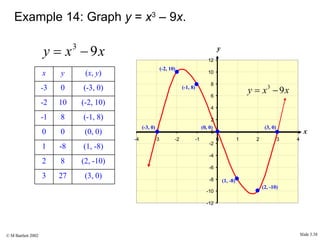
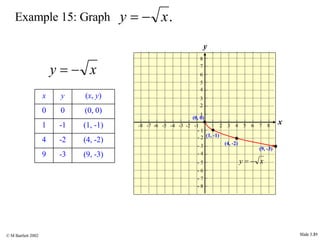
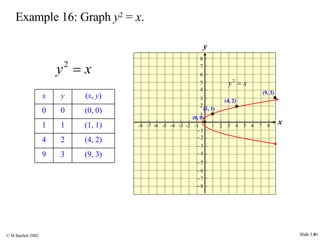
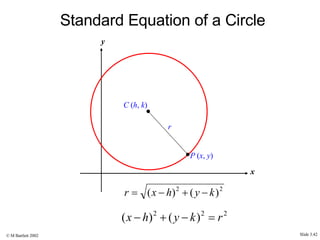
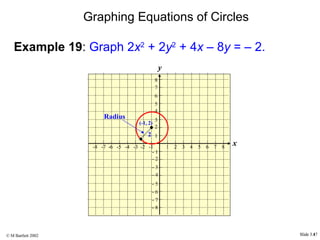
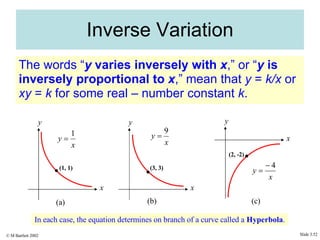
This document provides an overview of the rectangular coordinate system and linear equations. It introduces the key concepts of the coordinate plane, plotting points, determining slopes of lines, writing equations of lines in various forms (point-slope, slope-intercept, general), and identifying parallel and perpendicular lines. Examples are included throughout to demonstrate these linear algebra concepts.

1. 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y The Rectangular Coordinate System © M Bartlett 2002 Slide 3.1

2. 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y Quadrant I Quadrant II Quadrant III Quadrant IV Origin © M Bartlett 2002 Slide 3.2

3. 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y P (3, 3) Q ( – 4, 6) R (6, – 4) © M Bartlett 2002 Slide 3.3

4. (– 4, 6) (– 2, 5) (0, 4) (2, 3) (4, 2) © M Bartlett 2002 Slide 3.4 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (4, 2) 2 4 (2, 3) 3 2 (0, 4) 4 0 (– 2, 5) 5 – 2 (– 4, 6) 6 – 4 ( x , y ) y x

5. (– 4, – 9) (– 2, – 6) (0, – 3 ) (2, 0) (4, 3) © M Bartlett 2002 Slide 3.5 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (4, 3) 3 4 (2, 0) 0 2 (0, – 3) – 3 0 (– 2, – 6) – 6 – 2 (– 4, – 9) – 9 – 4 ( x , y ) y x

6. (4, 0) (0, 1 ) (– 4, 2) © M Bartlett 2002 Slide 3.6 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (4, 0) 0 4 (2, ) 2 (0, 1) 1 0 (– 2, ) – 2 (– 4, 2) 2 – 4 ( x , y ) y x (2, ) (2, )

7. (– 3, 2) (– 1, 2) (0, 2 ) (2, 2) (4, 2) © M Bartlett 2002 Slide 3.7 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (4, 2) 2 4 (2, 2) 2 2 (0, 2) 2 0 (– 1, 2) 2 – 1 (– 3, 2) 2 – 3 ( x , y ) y x

8. (– 3, – 4) (– 3, – 2) (– 3, 0) (– 3, 2) (– 3, 4) © M Bartlett 2002 Slide 3.8 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (– 3, 4) 4 – 3 (– 3, 2) 2 – 3 (– 3, 0) 0 – 3 (– 3, – 2) – 2 – 3 (– 3, – 4) – 4 – 3 ( x , y ) y x

9. APPLICATION Example 1: A car purchased for $17,000 is expected to depreciate according to the formula y = – 1,360 x + 17,000. When will the car be worthless? © M Bartlett 2002 Slide 3.9 Solution : The car is worthless when y = 0. – 1360 x + 17000 = 0 17000 = 1360 x +1360 x +1360 x x = 12.5 The car will be worthless in 12.5 years.

10. The Distance Formula d | x 2 – x 1 | | y 2 – y 1 | x y © M Bartlett 2002 Slide 3.10

11. The Midpoint Formula © M Bartlett 2002 Slide 3.11 x y

12. Slope of a Line Suppose that a college student rents a room for $300 per month, plus a $200 non-refundable deposit. Construct a table that shows the cost ( y ) for different numbers of months ( x ). Construct a graph from this data. © M Bartlett 2002 Slide 3.12 1,400 4 1,100 3 800 2 500 1 200 0 Total Cost ( y ) Time in Months ( x )

13. The Slope of a Non-vertical Line x 2 – x 1 y 2 – y 1 © M Bartlett 2002 Slide 3.13 x y

14. EXAMPLE 1 : Find the slope of the line passing through P(–1, –2) and Q(7, 8). P (–1, –2) Q (7, 8) Run = 8 R (7, –2) Rise = 10 © M Bartlett 2002 Slide 3.14 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

15. EXAMPLE 2 : Find the slope of the line determined by 3x – 2y =9. P (0, –4.5) Q (3, 0) R (3, –4.5) x = 0 , y = – 4.5 y = 0, x = 3 Rise = 4.5 Run = 3 © M Bartlett 2002 Slide 3.15 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

16. Exampe 3 : If carpet cost $25 per square yard plus a delivery charge of $30, the total cost c of n yards is given by the formula Total cost equals cost per square yard times The number of square yards purchased plus the delivery charge © M Bartlett 2002 Slide 3.16

17. Slope = 0 Slope undefined © M Bartlett 2002 Slide 3.17 x y x y

18. Positive Slope Negative Slope © M Bartlett 2002 Slide 3.18 x y x y

19. The Slope of Parallel Lines A C B Slope = m 1 D F E Slope = m 2 © M Bartlett 2002 Slide 3.19 x y

20. EXAMPLE 4 : The lines in the figure below are parallel. Find x. R (–2, 5) T ( x , 0) Q (–3, 4) P (1, –2) Slope of PQ = slope of RT © M Bartlett 2002 Slide 3.20 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

21. The Slope of Perpendicular Lines P ( a , b ) Slope = m 1 O (0, 0) Q ( c , d ) Slope = m 2 © M Bartlett 2002 Slide 3.21 x y

22. EXAMPLE 5 : Are the lines shown in the figure below perpendicular? Q (9, 4) O (0, 0) P (3, –4) © M Bartlett 2002 Slide 3.22 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

23. Point – Slope of the Equation of a Line Δ x = x – x 1 © M Bartlett 2002 Slide 3.23 Slope = m Δ y = y – y 1 y – y 1 = m ( x – x 1 ) x y

24. EXAMPLE 5 : Write the equation of the line with slope passing through P(–4, 5). P (–4, 5) © M Bartlett 2002 Slide 3.24 Q ( x , y ) Run = 3 Rise = – 2 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

25. EXAMPLE 6 : Find the equation of the line passing through P(–5, 4) and Q(8, –6). P (–5, 4) Run = 13 Q (8, –6) Rise = -10 © M Bartlett 2002 Slide 3.25 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

26. Slope – Intercept Form of the Equation of a Line © M Bartlett 2002 Slide 3.26 Slope = m y - intercept x y

27. Graphing Equations Written in Slope – Intercept Form © M Bartlett 2002 Slide 3.27 P (0, –2) Q (3, 2) Δ x = 3 Δ y = 4 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

28. Example 7 : Find the slope and the y – intercept of the line with equation 2( x – 3) = – 3( y + 5). Then graph it. 2 x – 6 = – 3 y – 15 3 y – 6 = – 2 x – 15 3 y = – 2 x – 9 y – intercept is (0, – 3) 3 – 2 (0, –3) (3, –5) 2( x – 3) = – 3( y + 5) Slide 3.28 © M Bartlett 2002 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

29. Example 8 : Are the lines represented by the equations y = 3 x + 2 and 6 x + 2 y = 5 parallel? Example 9 : Are the lines represented by the equations 2 x + 3 y = 9 and 3 x – 2 y = 5 perpendicular? Example 10 : Write the equation of the line passing through P (1, 2) and parallel to the line y = 8 x – 3. Example 11 : Write the equation of the line passing through Q (1, 2) and perpendicular to the line y = 8 x – 3. Slide 3.29 © M Bartlett 2002

30. General Form of the Equation of a Line If A , B , and C are real numbers and B ≠ 0, the graph of Ax + By = C (General Form of the equation of a line.) is a non-vertical line with slope of and a y – intercept of . If B = 0, the graph is a vertical line with x – intercept of . Slide 3.30 © M Bartlett 2002

31. Example 12 : Find the slope and y – intercept of the graph of 3 x – 4 y = 12. Slide 3.31 © M Bartlett 2002 Solution: Step 3: Step 4: Step 1: Step 2:

32. Summary General Form A x + B y = C A and B cannot both be 0. Slope – intercept form y = mx + b The slope m , and the y -intercept is (0, b ). Point – slope form y – y 1 = m ( x – x 1 ) The slope is m , and the line passes through ( x 1 , y 1 ). A horizontal line y = b The slope is 0, and the y intercept is (0, b ). A vertical Line x = a There is no defined slope, and the x -intercept is ( a , 0). Slide 3.32 © M Bartlett 2002

33. Example 13 : A taxi cab was purchased for $24,300. Its salvage value at the end of its 7-year useful life is expected to be $1,900. If y is the value of the taxi cab after x -years of use, and y and x are related by the equation of a line, a. Find the equation of the line, called the depreciation equation . b. Find the value of the taxi cab after 3 years. c. Find the economic meaning of the y -intercept of the line. d. Find the economic meaning of the slope of the line. Slide 3.33 © M Bartlett 2002

34. © M Bartlett 2002 Slide 3.34 Intercepts of Graphs x -intercepts y -intercept x y x y

35. Graphing an Equation © M Bartlett 2002 Slide 3.1 Slide 3.35 (-3, 5) (-2, 0) (-1, -3) (1, -3) (2, 0) (3, 5) V (0, -4) This is an example of a Parabola . The lowest point being the vertex V (0,– 4). Since the y – axis divides the graph into two congruent halves it is called the axis of symmetry . The parabola is symmetric about the y – axis . 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (3, 5) 5 3 (2, 0) 0 2 (1, -3) -3 1 (0, -4) -4 0 (-1, -3) -3 -1 (-2, 0) 0 -2 (-3, 5) 5 -3 ( x , y ) y x

36. © M Bartlett 2002 Slide 3.36 Symmetries of Graphs y – axis symmetry Origin symmetry x – axis symmetry x y x y x y

37. Absolute – Value Graph © M Bartlett 2002 Slide 3.1 Slide 3.37 (1, 1) (2, 2) (0, 0) (3, 3) (4, 4) 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (4, 4) 4 4 (3, 3) 3 3 (2, 2) 2 2 (1, 1) 1 1 (0, 0) 0 0 ( x , y ) y x

38. Example 14: Graph y = x 3 – 9 x . (-3, 0) (-2, 10) (-1, 8) (0, 0) (1, -8) (2, -10) (3, 0) © M Bartlett 2002 Slide 3.38 y x (3, 0) 27 3 (2, -10) 8 2 (1, -8) -8 1 (0, 0) 0 0 (-1, 8) 8 -1 (-2, 10) 10 -2 (-3, 0) 0 -3 ( x , y ) y x

39. © M Bartlett 2002 Slide 3.1 Slide 3.39 (1, -1) (4, -2) (0, 0) (9, -3) 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (9, -3) -3 9 (4, -2) -2 4 (1, -1) -1 1 (0, 0) 0 0 ( x , y ) y x Example 15: Graph

40. © M Bartlett 2002 Slide 3.1 Slide 3.40 (1, 1) (4, 2) (0, 0) (9, 3) Example 16: Graph y 2 = x . 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y (9, 3) 3 9 (4, 2) 2 4 (1, 1) 1 1 (0, 0) 0 0 ( x , y ) y x

41. Circles A circle is the set of all points in a plane that are a fixed distance from a point called the center . The fixed distance is called the radius of the circle . © M Bartlett 2002 Slide 3.41

42. Standard Equation of a Circle C ( h , k ) P ( x , y ) r © M Bartlett 2002 Slide 3.42 y x

43. The Standard Equation of a Circle with Center at ( h , k ) The graph of any equation that can be written in the form ( x – h ) 2 + ( y – k ) 2 = r 2 is a circle of radius r and center at point ( h , k ). © M Bartlett 2002 Slide 3.43

44. The Standard Equation of a Circle with Center at (0, 0) The graph of any equation that can be written in the form x 2 + y 2 = r 2 is a circle of radius r and center at the origin. The general form of the equation of a circle is given by x 2 + y 2 + cx + dy + e = 0 where c , d , and e are real numbers. © M Bartlett 2002 Slide 3.44

45. Example 17 : Find the general form of the equation of the circle with radius 6 and center at (– 2, 5). Slide 3.45 © M Bartlett 2002 Solution : ( x – h ) 2 + ( y – k ) 2 = r 2

46. Example 18 : Find the general form of the equation of a circle with endpoints of its diameter at (– 2, 2) and (6, 8). Slide 3.46 © M Bartlett 2002

47. Graphing Equations of Circles © M Bartlett 2002 Slide 3.1 Slide 3.47 (-1, 2) Example 19 : Graph 2 x 2 + 2 y 2 + 4 x – 8 y = – 2. Radius 2 1 2 3 4 5 6 7 8 -8 -7 -6 -5 -4 -3 -2 -1 8 7 6 5 4 3 2 1 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 x y

48. Proportions is called a Proportion. The numbers a and d are called the extremes . The numbers b and c are called the means . © M Bartlett 2002 Slide 3.48

49. Property of Proportions © M Bartlett 2002 Slide 3.49 In any proportion, the product of the extremes is equal to the product of the means. Example 21 : The ratio of women to men in a mathematics class is 3 to 5. How many women are in the class if there are 30 men? Example 20 : Solve the proportion

50. Direct Variation The words “ y varies directly with x ,” or “ y is directly proportional to x ,” mean that y = kx for some real – number constant k . The number k is called the constant of proportionality. © M Bartlett 2002 Slide 3.50 m = 2 m = 1 y x

51. Example 22 : The distance that an object will fall in t seconds varies directly with the square of t . An object falls 16 feet in 1 second. How long will it take to fall 144 feet? Slide 3.51 © M Bartlett 2002

52. Inverse Variation © M Bartlett 2002 Slide 3.52 The words “ y varies inversely with x ,” or “ y is inversely proportional to x ,” mean that y = k/x or xy = k for some real – number constant k . (1, 1) (3, 3) (2, -2) In each case, the equation determines on branch of a curve called a Hyperbola . y x (c) y x (a) y x (b)

53. Example 23 : Intensity of illumination from a light source varies inversely with the square of the distance from the source. If the intensity of the light source is 100 lumens at a distance of 20 feet, find the intensity at 30 feet. Slide 3.53 © M Bartlett 2002

54. Joint Variation © M Bartlett 2002 Slide 3.54 The words “ y varies jointly with w and x ” mean that y = kwx for some real – number constant k .

55. Example 24 : The area of a rectangle varies jointly with its length and width. Find the constant of proportionality. Slide 3.55 © M Bartlett 2002

56. Combined Variation © M Bartlett 2002 Slide 3.56 y varies directly with x and inversely with z . y varies jointly with the square of x and the cube root of z . y varies jointly with x and the square root of z and inversely with the cube root of t . y varies inversely with the product of x and z .

57. Example 25 : The power, in watts, dissipated as heat in a resistor varies directly with the square of the voltage and inversely with the resistance. If 20 volts are placed across a 20-ohm resistor, it will dissipate 20 watts. What voltage across a 10-ohm resistor will dissipate 40 watts? Slide 3.57 © M Bartlett 2002