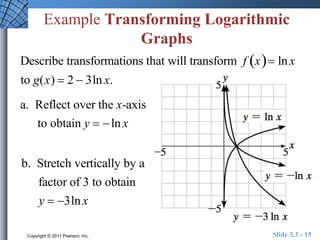
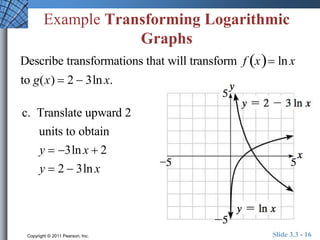
The document discusses logarithmic functions and their graphs. It introduces common logarithms with base 10 and natural logarithms with base e. It explains how to change between logarithmic and exponential form and explores various properties of logarithms. Additionally, it discusses how logarithms are used to measure sound intensity in decibels and provides examples of solving logarithmic equations and transforming logarithmic graphs.

1. 3.3
Logarithmic
Functions and
Their Graphs
Copyright © 2011 Pearson, Inc.

2. What you’ll learn about
 Inverses of Exponential Functions
 Common Logarithms – Base 10
 Natural Logarithms – Base e
 Graphs of Logarithmic Functions
 Measuring Sound Using Decibels
… and why
Logarithmic functions are used in many applications,
including the measurement of the relative intensity of
sounds.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 2

3. Changing Between Logarithmic and
Exponential Form
If x  0 and 0  b  1, then
y  logb (x) if and only if by  x.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 3

4. Inverses of Exponential Functions
Copyright © 2011 Pearson, Inc. Slide 3.3 - 4

5. Basic Properties of Logarithms
For 0  b  1, x  0, and any real number y.
g logb 1  0 because b0  1.
g logb b  1 because b1  b.
g logb by  y because by  by .
g blogb x  x because logb x  logb x.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 5

6. An Exponential Function and Its
Inverse
Copyright © 2011 Pearson, Inc. Slide 3.3 - 6

7. Common Logarithm – Base 10
 Logarithms with base 10 are called common
logarithms.
 The common logarithm log10x = log x.
 The common logarithm is the inverse of the
exponential function y = 10x.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 7

8. Basic Properties of Common
Logarithms
Let x and y be real numbers with x  0.
g log1  0 because 100  1.
g log10  1 because 101  10.
g log10y  y because 10y  10y.
g 10log x  x because log x  log x.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 8

9. Example Solving Simple Logarithmic
Equations
Solve the equation by changing it to exponential form.
log x  4
Copyright © 2011 Pearson, Inc. Slide 3.3 - 9

10. Example Solving Simple Logarithmic
Equations
Solve the equation by changing it to exponential form.
log x  4
x  104  10,000
Copyright © 2011 Pearson, Inc. Slide 3.3 - 10

11. Basic Properties of Natural Logarithms
Let x and y be real numbers with x  0.
g ln1  0 because e0  1.
g lne  1 because e1  e.
g lney  y because ey  ey .
g eln x  x because ln x  ln x.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 11

12. Graphs of the Common and Natural
Logarithm
Copyright © 2011 Pearson, Inc. Slide 3.3 - 12

13. Example Transforming Logarithmic
Graphs
Describe transformations that will transform f x ln x
to g(x)  2  3ln x.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 13

14. Example Transforming Logarithmic
Graphs
Describe transformations that will transform f x ln x
to g(x)  2  3ln x.
Solve Algebraically
g(x)  2  3ln x
 3ln x  2
  f x 2
So g can be obtained by reflecting the graph of f across
the x-axis, stretching vertically by a factor of 3, and then
shifting upward 2 units.
Copyright © 2011 Pearson, Inc. Slide 3.3 - 14

15. Example Transforming Logarithmic
Graphs
Describe transformations that will transform f x ln x
to g(x)  2  3ln x.
a. Reflect over the x-axis
to obtain y   ln x
b. Stretch vertically by a
factor of 3 to obtain
y  3ln x
Copyright © 2011 Pearson, Inc. Slide 3.3 - 15

16. Example Transforming Logarithmic
Graphs
Describe transformations that will transform f x ln x
to g(x)  2  3ln x.
c. Translate upward 2
units to obtain
y  3ln x  2
y  2  3ln x
Copyright © 2011 Pearson, Inc. Slide 3.3 - 16

17. Decibels
The level of sound intensity in decibels (dB) is
  10log
I
I0

 

 ,
where  (beta) is the number of decibels,
I is the sound intensity in W/m2 , and
I0  1012 W/m2 is the threshold of human
hearing (the quietest audible sound intensity).
Copyright © 2011 Pearson, Inc. Slide 3.3 - 17

18. Quick Review
Evaluate the expression without using a calculator.
1. 6-2
2.
811
232
3. 70
Rewrite as a base raised to a rational number exponent.
4.
1
e3
5. 10 4
Copyright © 2011 Pearson, Inc. Slide 3.3 - 18

19. Quick Review Solutions
Evaluate the expression without using a calculator.
1. 6-2
1
36
2.
811
232 2
3. 70 1
Rewrite as a base raised to a rational number exponent.
4.
1
e3
e3/2
5. 10 4 101/4
Copyright © 2011 Pearson, Inc. Slide 3.3 - 19