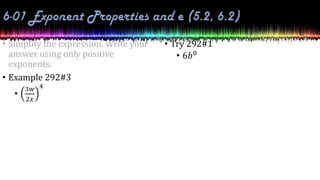
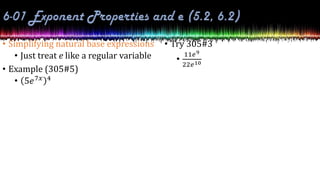
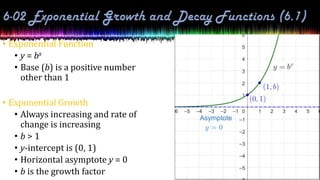
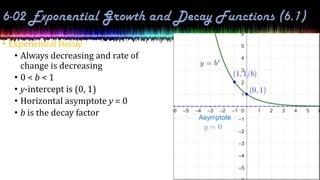
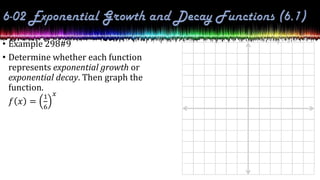
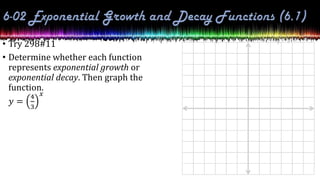
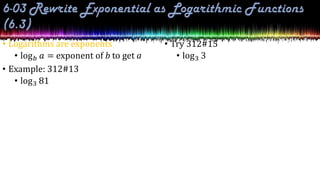
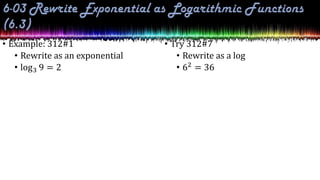
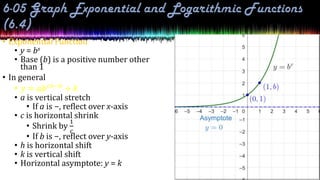
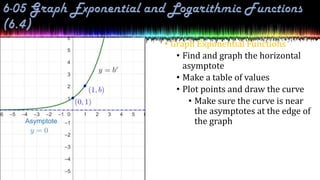
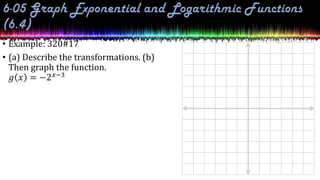
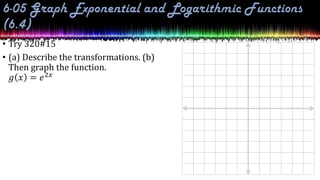
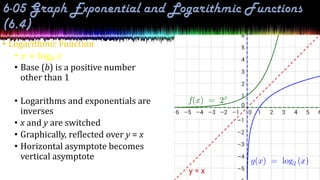
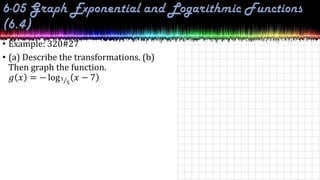
This document provides information about exponential and logarithmic functions including:
- Properties of exponents and logarithms
- Graphing exponential and logarithmic functions
- Solving exponential and logarithmic equations
- Using regression analysis to determine an exponential or logarithmic model from data points