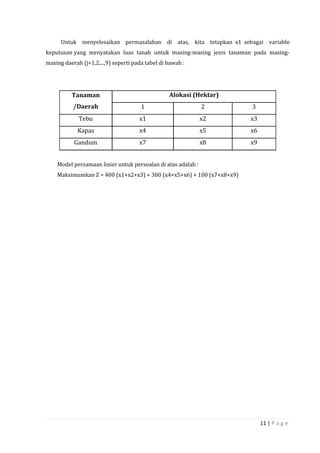
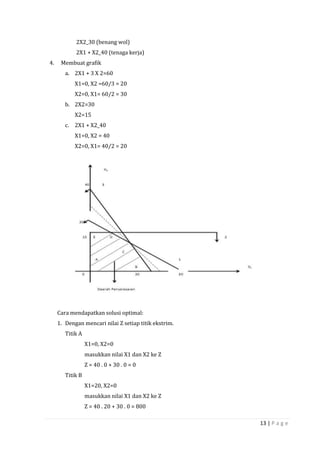
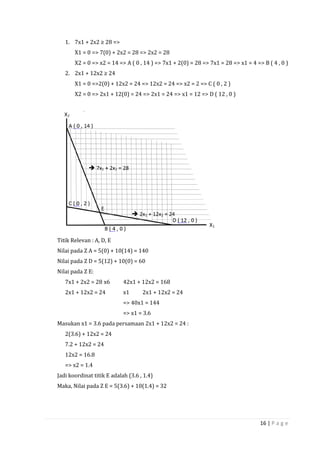
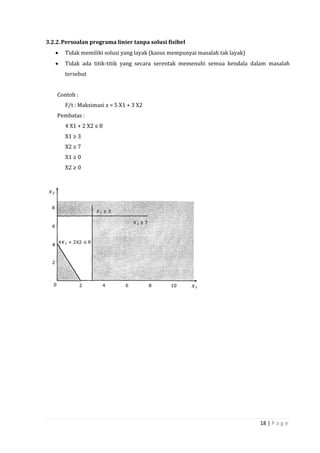
Dokumen ini adalah panduan tentang penelitian operasional dan teknik pengambilan keputusan, disusun oleh dosen dan mahasiswa di Fakultas Ekonomi Universitas Krisnadwipayana. Terdapat ringkasan mengenai sejarah, model-model serta metodologi penelitian operasional, termasuk program linier, teori dualitas, dan proses keputusan. Buku ini bertujuan untuk memberikan pemahaman menyeluruh dalam aplikasi riset operasional dalam berbagai masalah manajerial.