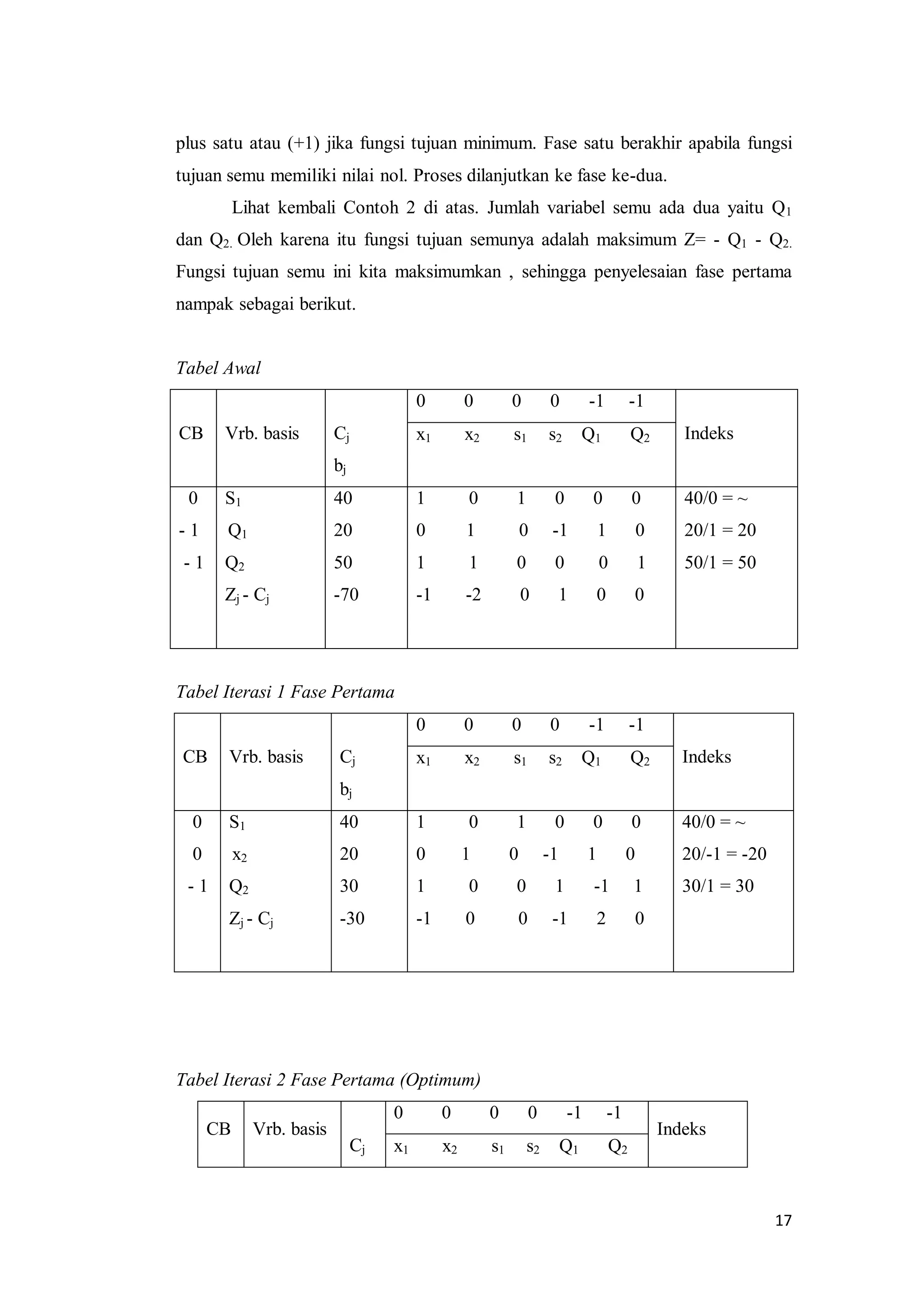
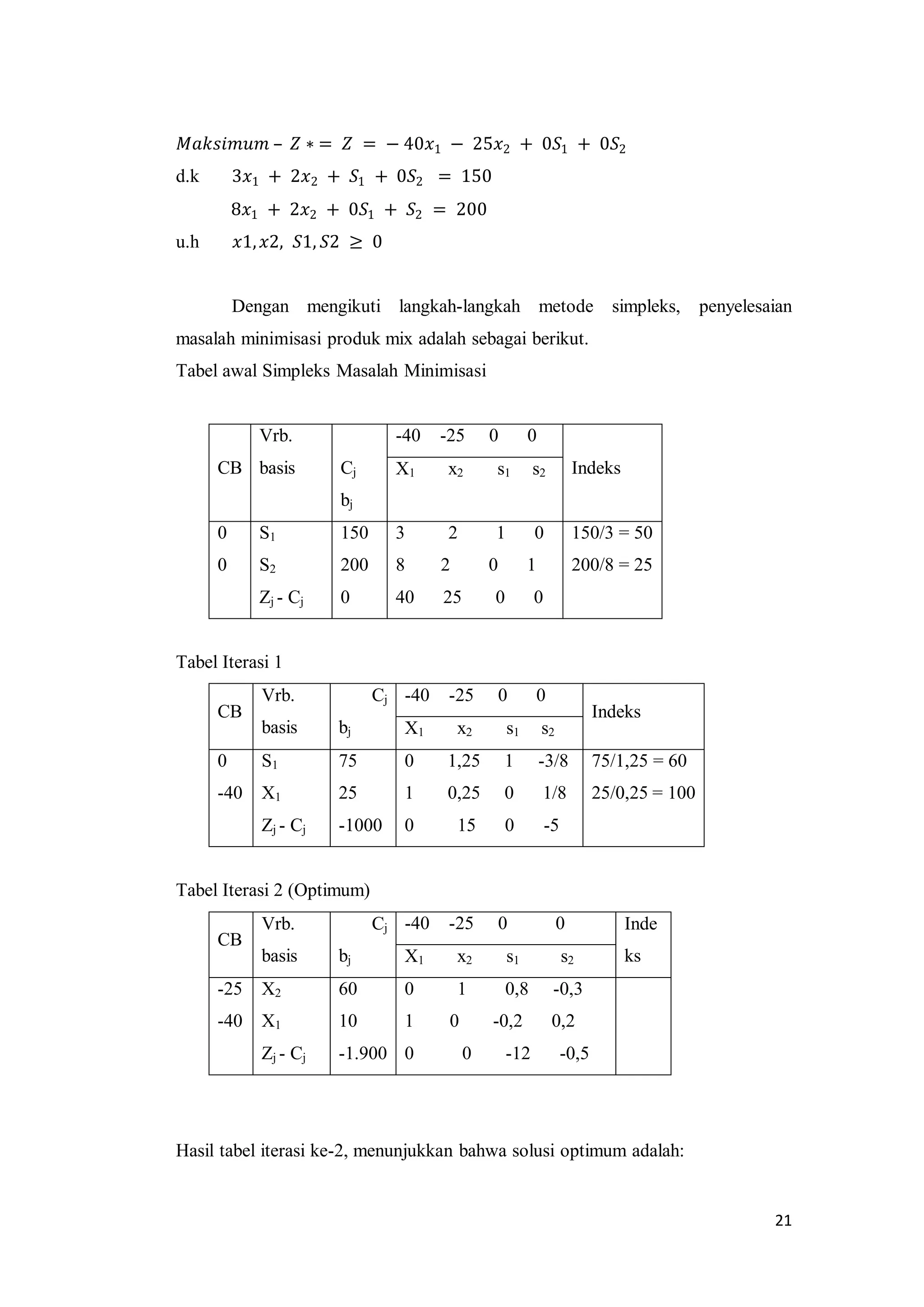
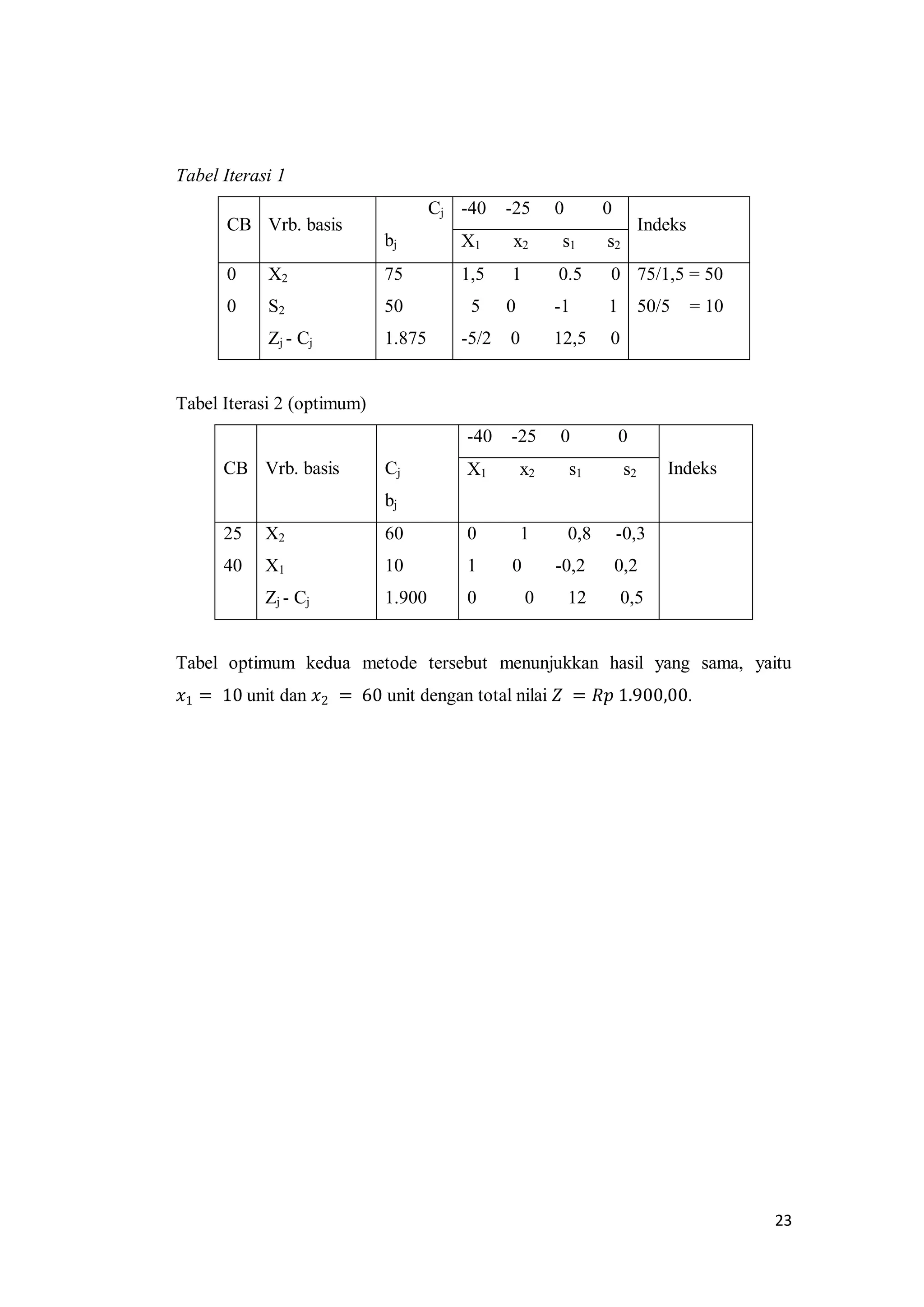
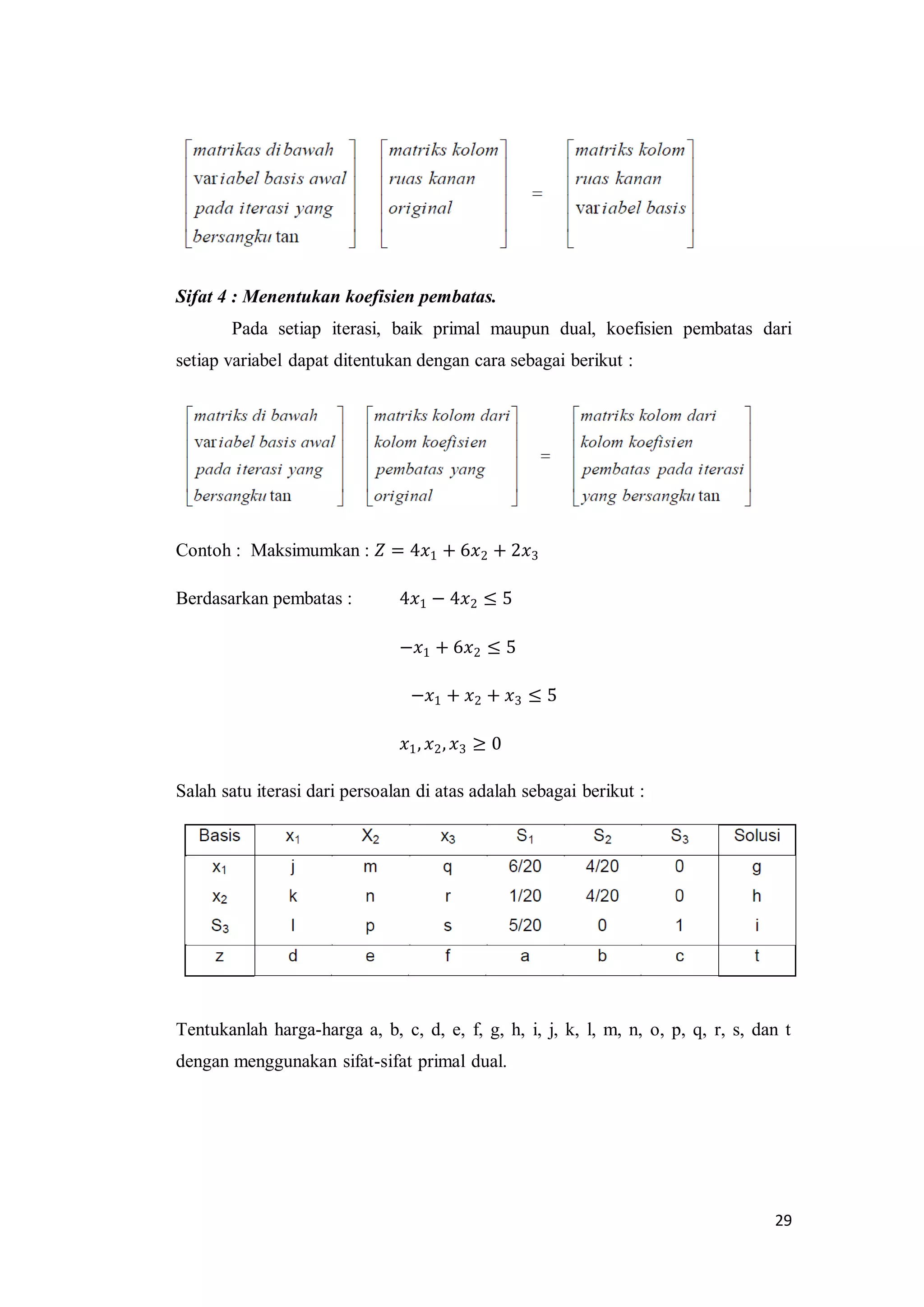
Dokumen ini adalah makalah tentang metode simpleks dalam pemrograman linear yang disusun oleh kelompok 4 dari Universitas Negeri Medan. Makalah ini menjelaskan konsep dasar pemrograman linear, termasuk masalah maksimasi dan minimasi, serta langkah-langkah penggunaan metode simpleks untuk mencapai solusi optimal. Selain itu, dokumen ini juga membahas masalah yang terkait dengan kendala bertanda '=' serta metode penyelesaiannya.








![9
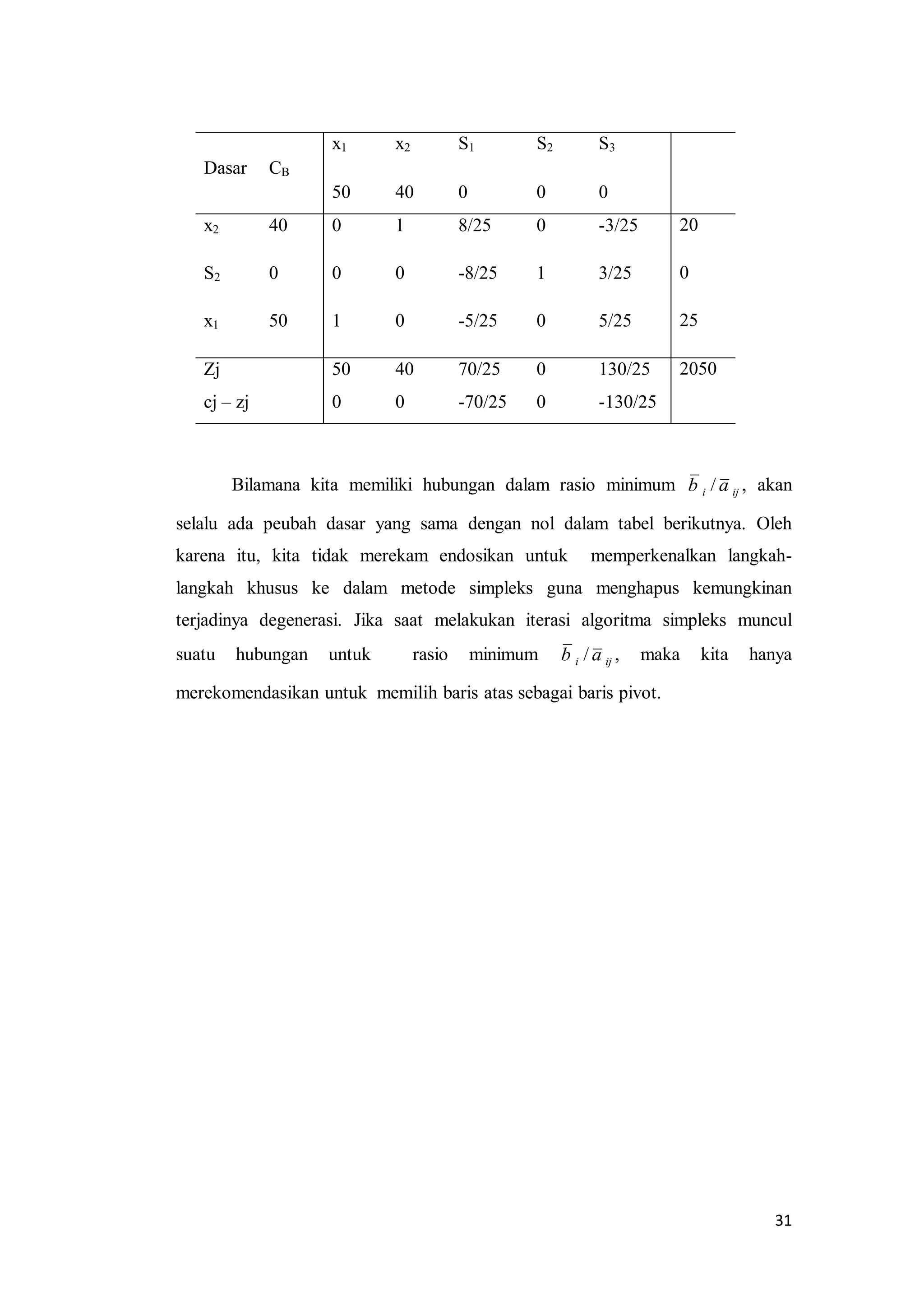
Variabel Dasar Z 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 NK
Keterangan
(indeks)
𝑍 1 -3 -5 0 0 0 0
𝑥3 0 2 0 1 0 0 8 8/0 = ∞
𝑥4 0 0 3 0 1 0 15 15/3 = 5
𝑥5 0 6 5 0 0 1 30 30/5 = 6
Z
𝑥3
𝑥2 0 0 1 0 1/3 0 15/3
𝑥5
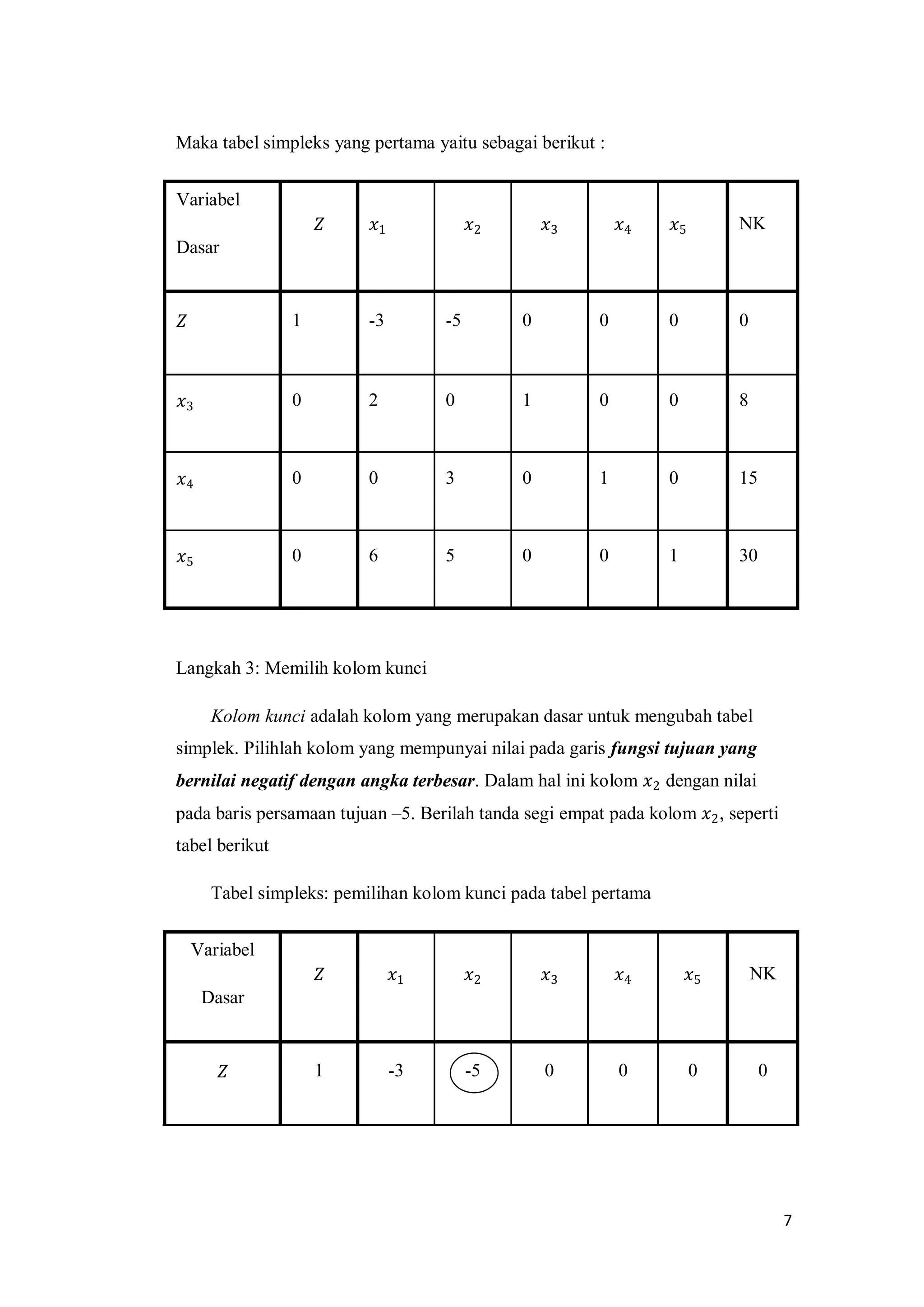
Langkah 6: Mengubah nilai-nilai selain pada baris kunci
Dengan menggunakan rumus berikut
𝐵𝑎𝑟𝑖𝑠 𝑏𝑎𝑟𝑢 = 𝑏𝑎𝑟𝑖𝑠 𝑙𝑎𝑚𝑎 − 𝑘𝑜𝑒𝑓𝑖𝑠𝑖𝑒𝑛 𝑝𝑎𝑑𝑎 𝑘𝑜𝑙𝑜𝑚 𝑘𝑢𝑛𝑐𝑖
× 𝑛𝑖𝑙𝑎𝑖 𝑏𝑎𝑟𝑢 𝑏𝑎𝑟𝑖𝑠 𝑘𝑢𝑛𝑐𝑖
Baris pertama (Z)
[-3 -5 0 0 0, 0 ]](https://image.slidesharecdn.com/makalahkelompok4metodesimpleks-150526013011-lva1-app6892/75/Makalah-kelompok-4-metode-simpleks-10-2048.jpg)
![10
(-5) [ 0 1 0 1/3 0, 5 ] ( - )
Nilai baru = [-3 0 0 5/3 0, 25]
Baris ke-2 (batasan 1)
[2 0 1 0 0, 8 ]
(0) [ 0 1 0 1/3 0, 5 ] ( - )
Nilai baru = [2 0 1 0 0, 8]
Baris ke-4 (batasan 3)
[ 6 5 0 0 1, 30 ]
(5) [ 0 1 0 1/3 0, 5 ] ( - )
Nilai baru = [ 6 0 0 -5/3 1, 5 ]
Tabel pertama nilai lama dan tabel kedua nilai baru
Variabel Dasar 𝑍 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 NK
Z 1 -3 -5 0 0 0 0
𝑥3 0 2 0 1 0 0 8
𝑥4 0 0 3 0 1 0 15](https://image.slidesharecdn.com/makalahkelompok4metodesimpleks-150526013011-lva1-app6892/75/Makalah-kelompok-4-metode-simpleks-11-2048.jpg)
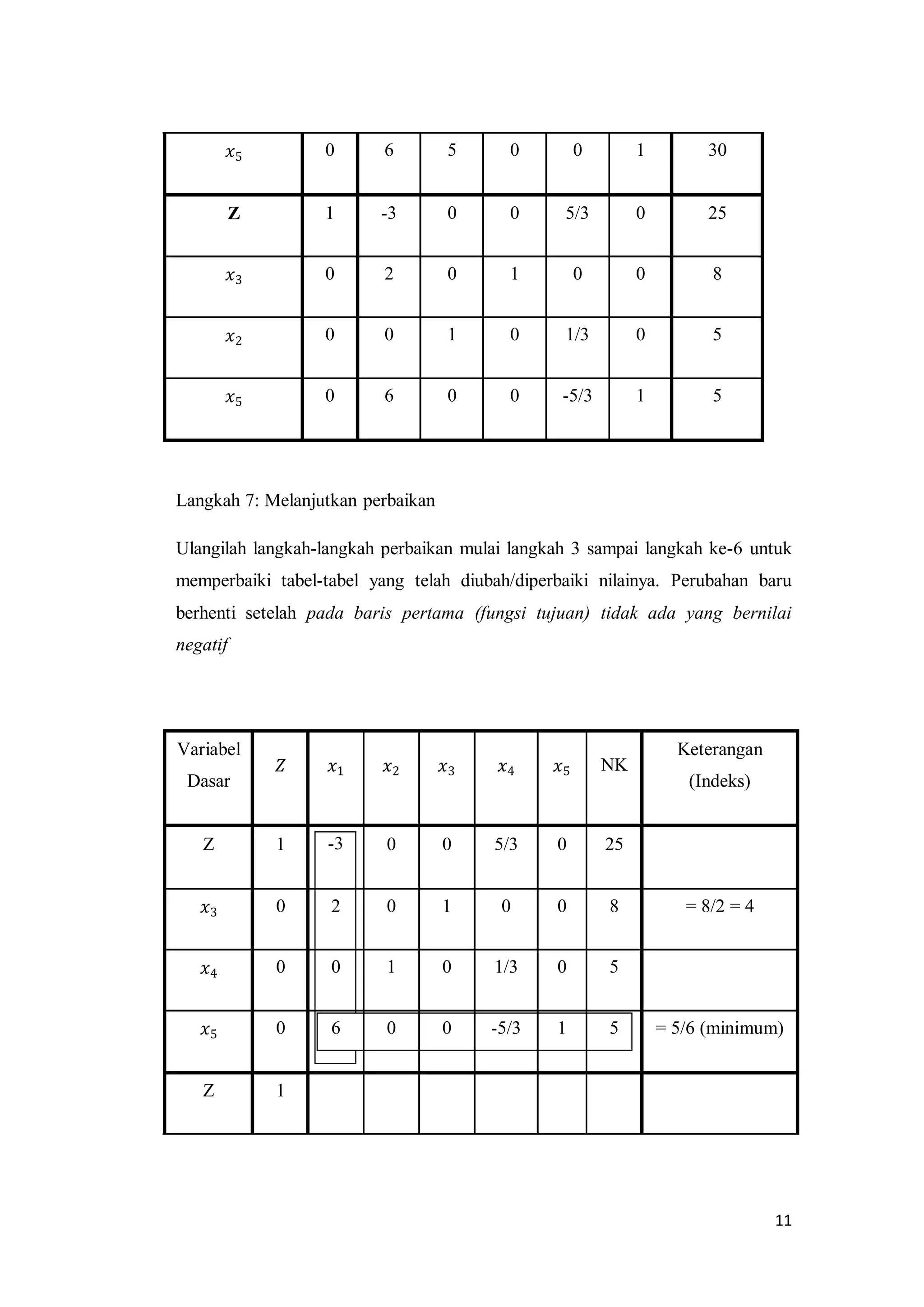
![12
𝑥3 0
𝑥2 0
𝑥1 0 6/6 0 0 -5/18 1/6 5/6
Nilai baru
Baris ke-1
[-3 0 0 5/3 0, 25 ]
(-3) [ 1 0 0 -5/18 1/6, 5/6] ( - )
Nilai baru = [ 0 0 0 5/6 ½, 271
/2]
Baris ke-2 (batasan 1)
[ 2 0 1 0 0, 8 ]
(2) [ 1 0 0 -5/18 1/6, 5/6] ( - )
Nilai baru = 0 0 1 5/9 -1/3, 61
/3]
Baris ke-3 tidak berubah karena nilai pada kolom kunci = 0
[ 0 1 0 1/3 0, 5 ]
(0) [ 1 0 0 -5/18 1/6, 5/6] ( - )](https://image.slidesharecdn.com/makalahkelompok4metodesimpleks-150526013011-lva1-app6892/75/Makalah-kelompok-4-metode-simpleks-13-2048.jpg)
![13
Nilai baru = 0 1 0 1/3 0, 5]
Tabel simpleks final hasil perubahan
Variabel
Dasar
𝑍 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 NK
Z 1 0 0 0 5/6 ½ 271
/2
𝑥3 0 0 0 1 5/9 -1/3 61
/3
𝑥2 0 0 1 0 1/3 0 5
𝑥1 0 1 0 0 -5/18 1/6 5/6
Baris pertama (Z) tidak ada lagi yang bernilai negatif. Sehingga tabel tidak dapat
dioptimalkan lagi dan tabel tersebut merupakan hasil optimal
Dari tabel final didapat
𝑥1 =
5
6
𝑥2 = 5
𝑍 𝑚𝑎𝑘𝑠𝑖𝑚𝑢𝑚 = 27
1
2](https://image.slidesharecdn.com/makalahkelompok4metodesimpleks-150526013011-lva1-app6892/75/Makalah-kelompok-4-metode-simpleks-14-2048.jpg)

![15
Tabel awal simpleks dapat dibuat seperti berikut ini:
Tabel awal simpleks Metode M besar
CB Vrb. basis
Cj
bj
50 80 0 0 -M -
M
Indeks
X1 x2 s1 s2 Q1
Q2
0
-M
-M
S1
Q1
Q2
Zj - Cj
40
20
50
-70M
1 0 1 0 0 0
0 1 0 -1 1 0
1 1 0 0 0 1
-M-50 -2M-80 0 M 0
0
40/0 = ~
20/1 =
20
50/1 =
50
Nilai yang terdapat pada baris Zj – Cj Tabel di atas diisi dengan menggunakan
cara sebagai berikut:
Z = [0, -M, -M]
40
20
50
- 0 = 0 – 20M – 50M = - 70M
Z1 = [0, -M, -M]
1
0
1
- 50 = 0 – M – 50 = - M - 50
Z2 = [0, -M, -M]
0
1
1
- 80 = 0 – M – M - 80 = - 2M - 80
Z4 = [0, -M, -M]
0
−1
0
- 0 = 0 + M + 0 = M
Dan seterusnya.
Dengan mengikuti langkah-langkah metode simpleks terdahulu,
penyelesaian contoh ke-2 dapat dilihat berikut ini.
Tabel iterasi 1](https://image.slidesharecdn.com/makalahkelompok4metodesimpleks-150526013011-lva1-app6892/75/Makalah-kelompok-4-metode-simpleks-16-2048.jpg)