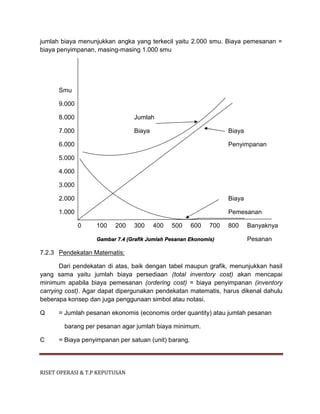
Dokumen ini merupakan rangkuman perkuliahan mengenai riset operasi dan teori pengambilan keputusan yang disusun oleh Andre Aurizt dalam semester lima di Universitas Krisnadwipayana. Berbagai tema diulas seperti asal-usul riset operasi, biaya dan analisis laba, perumusan masalah, serta aplikasi teori permainan dan antrian. Harapannya, rangkuman ini dapat memberikan manfaat dan kritik konstruktif untuk perbaikan di masa mendatang.
























































































![RISET OPERASI & T.P KEPUTUSAN
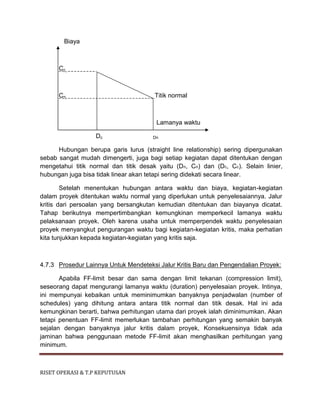
Cs = Satuan biaya kekurangan pesanan (unit cost of under-ordering) I,e, loss due
to not meeting the demand).
q = Banyaknya barang persediaan (stok).
C1 dan Cs merupakan kerugian (opportunity losses) yang disebabkan karena
jumlah persediaan kelebihan atau kekurangan sehingga tidak sama dengan jumlah
yang diminta.
Misalkan selanjutnya kita telah menentukan bahwa tepat sekali kalau
persediaan sebesar (q-1) unit. Akan kita pelajari apakah masih perlu untuk menambah
lagi. Untuk maksud ini kita harus menghitung expected incremental opportunity loss
atau (ΔL)* seandainya tidak ada penambahan atau ada penambahan satu unit.
Apabila ada tambahan satu unit ke dalam stok, tambahan ini memang
diperlukan seandainya barang yang dibutuhkan sebesar q unit atau lebih. Besarnya
nila (ΔL)* kalau tidak menambahkan ke dalam stok barang yang q, adalah sebagai
berikut:
(ΔL)* = CsPr (D ≥ q)
Penambahan satu unit tidak doperlukan kalau jumlah permintaan sebenarnya
kurang dari q. Besarnya (ΔL) untuk hal ini sebagai berikut:
(ΔL) = C1Pr (D < q)
Kalau (ΔL)* > (ΔL), kita harus menambah satu unit dalam stok, sebab
keputusan untuk tidak menambah menyebabkan kerugian yang lebih besar dari pada
menambah.
Dalam hal ini di mana (ΔL)* = (ΔL), pengambil keputusan dalam keadaan
indifference, artinya menambah atau tidak barang yang ke q akibat yang ditimbulkan
akan sama saja, yaitu:
CsPr (D ≥ q) = CiPr (D < q), ingat Pr (D ≥ q) + Pr (D < q) = 1
= C1[1 – Pr (D ≥ q)]
= C1 – C1 Pr (d ≥ q)
Sekarang mari kita definisikan probalita kritis Pc, sedemikian rupa sehingga Pc
= nilai Pr(D ≥ q), kalau (ΔL)* = (ΔL). Untuk mencari Pc, kita peroleh:](https://image.slidesharecdn.com/tugasuasrangkumanrisetoperasiandreaurizt1434021283-170925033528/85/Tugas-UAS-Rangkuman-Riset-Operasi-99-320.jpg)











![RISET OPERASI & T.P KEPUTUSAN
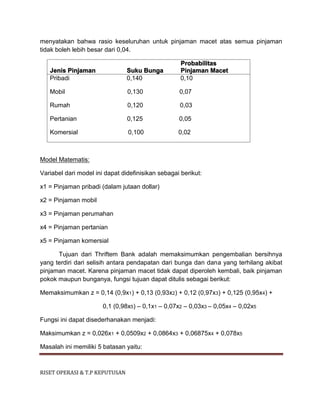
Batasan permintaan diekspresikan secara verbal sebagai berikut:
Jumlah kelebihan cat interior < 1 ton/hari
dibandingkan cat eksterior
[Permintaan akan cat interior] < 2 ton/hari
Secara matematis kedua batasan tersebut diekspresikan secara berturut-turut sebagai
berikut:
xI – xE < 1 [kelebihan cat interior dibandingkan eksterior]
xI < 2 [permintaan maksimum akan cat interior]
Batasan implisit (atau “yang harus dimengerti) adalah bahwa jumlah yang
diproduksi untuk setiap cat tidak dapat negative (kurang dari nol). Untuk menghindari
memperoleh pemecahan seperti itu, kita mengenakan batasan non negativitas, yang
secara normal ditulis sebagai berikut
xI > 0 (cat interior)
xE > 0 (cat eksterior)
Nilai-nilai variabel xE dan xI dikatakan merupakan pemecahan yang layak jika
memenuhi semua batasan dari model ini, termaksud batasan non negativitas.
Model matematis yang lengkap untuk masalah Reddy Mikks sekarang dapat
diringkas sebagai berikut:](https://image.slidesharecdn.com/tugasuasrangkumanrisetoperasiandreaurizt1434021283-170925033528/85/Tugas-UAS-Rangkuman-Riset-Operasi-112-320.jpg)