Uploaded byGem WeBlog
Topological Sorting (Decrease and Conquer)
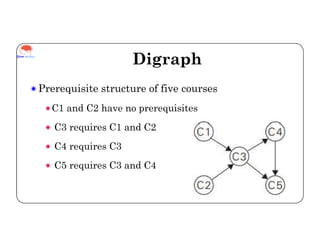
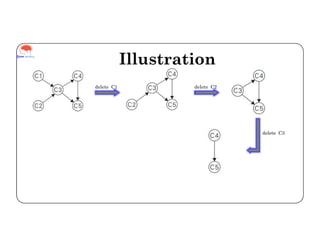
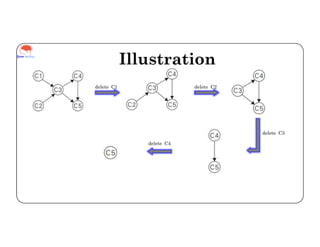
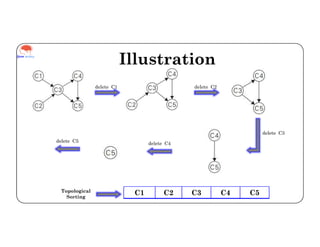
Topological sorting is a linear ordering of vertices in a directed acyclic graph. It is implemented using a decrease and conquer approach where the algorithm identifies a source vertex with no incoming edges, removes it from the graph, and repeats until all vertices are removed, outputting the order of deletions. The example shows the topological sorting of course prerequisites, where the algorithm iteratively deletes courses with all prerequisites completed until all courses are removed in a valid order of C1, C2, C3, C4, C5.
More Related Content
Similar to Topological Sorting (Decrease and Conquer)
Topological Sorting (Decrease and Conquer)
- 1. Topological Sorting Decrease andConquer Technique
- 2. Definition Topological sorting fora directed acyclic graph(DAG) Linear ordering of vertices For every edge U-V of a directed graph, For every edge U-V of a directed graph, Vertex u will come before vertex v in the ordering
- 3. Source Removal Algorithm Directimplementation of the decrease and conquers method Steps Identify a vertex(source) from a remaining digraph Identify a vertex(source) from a remaining digraph with no incoming edges If there are more than one such vertices, then break the tie randomly. Delete it along with all the edges outgoing from it Solution: deleted order of the vertices
- 4. Example Consider a setof 5 required courses {C1,C2,C3,C4,C5} a part-time student has to take in some degree program. The courses can be taken in any order as long as the following course prerequisites are met: C1 and C2 have no prerequisites C1 and C2 have no prerequisites C3 requires C1 and C2 C4 requires C3 C5 requires C3 and C4 The student can take only one course per term. In which order should the student take the courses?
- 5. Digraph Prerequisite structure offive courses C1 and C2 have no prerequisites C3 requires C1 and C2 C3 requires C1 and C2 C4 requires C3 C5 requires C3 and C4
- 6.
- 7.
- 8.
- 9. Illustration delete C1 deleteC2 C1 C2 Topological Sorting
- 10.
- 11. Illustration delete C1 deleteC2 delete C3 C1 C2 C3 Topological Sorting
- 12. Illustration delete C1 deleteC2 delete C3
- 13. Illustration delete C1 deleteC2 delete C3 delete C4 C1 C2 C3 C4 Topological Sorting
- 14. Illustration delete C1 deleteC2 delete C3 delete C4
- 15. Illustration delete C1 deleteC2 delete C3 delete C4 delete C5 C1 C2 C3 C4 C5 Topological Sorting