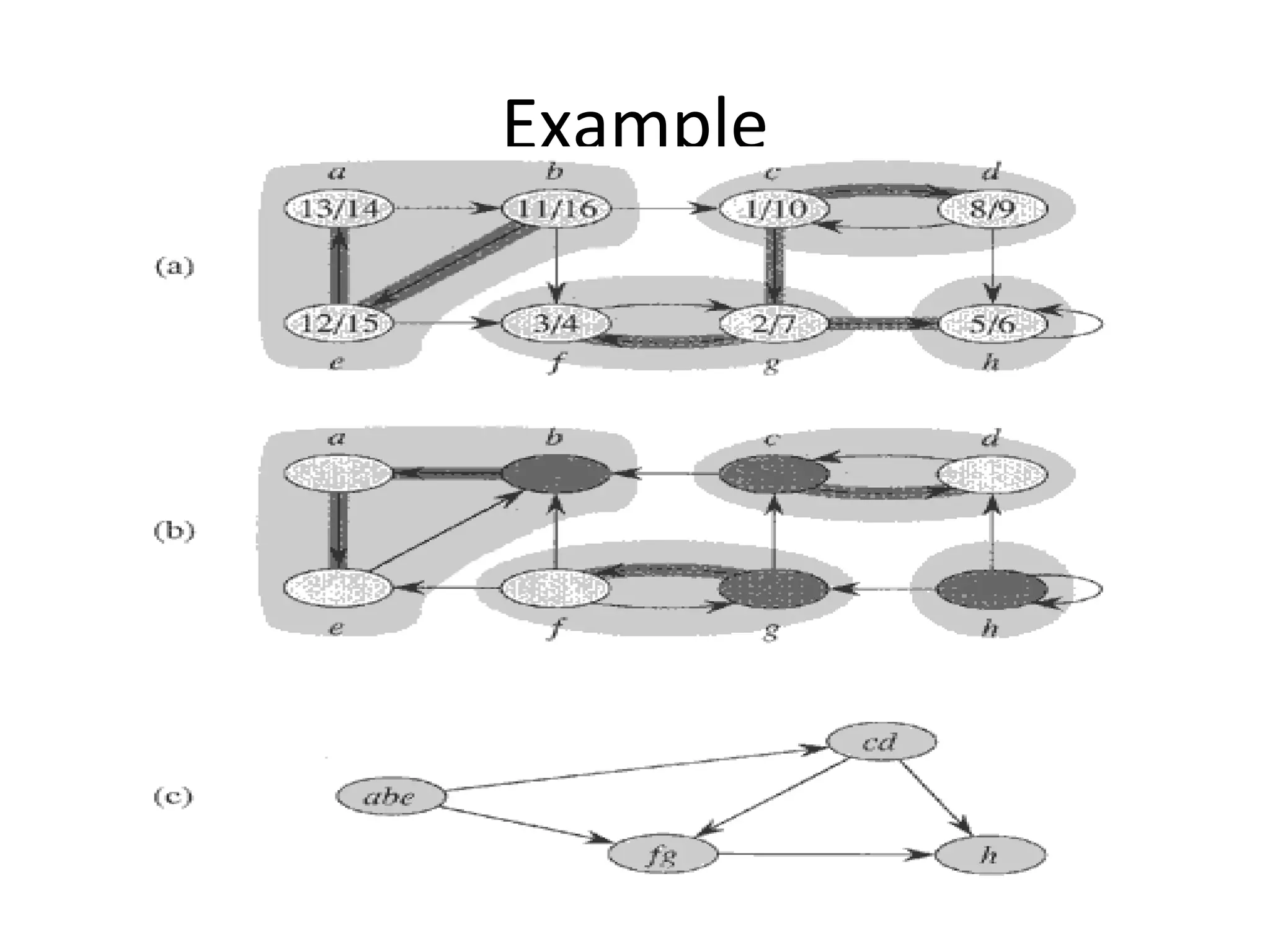
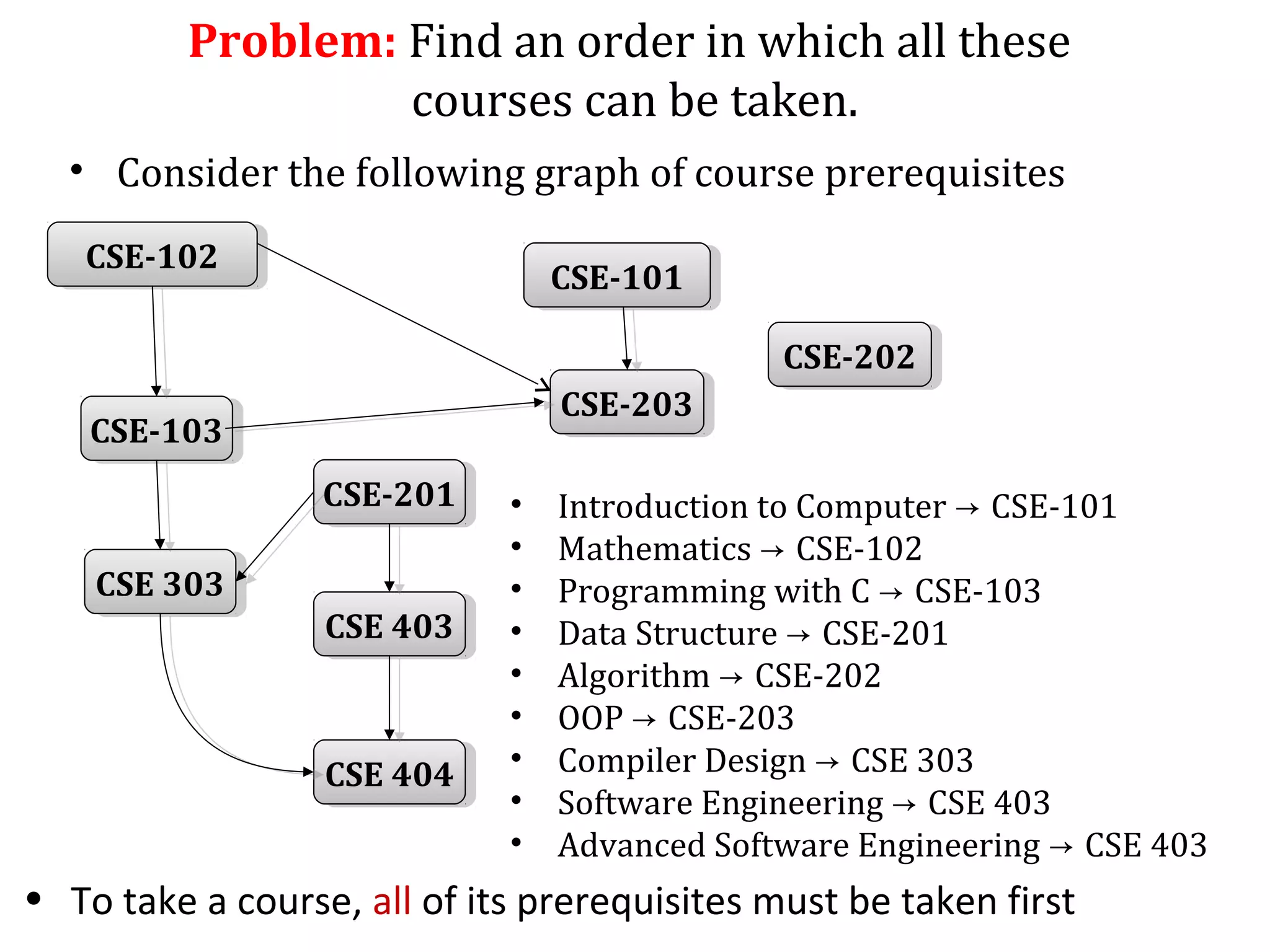
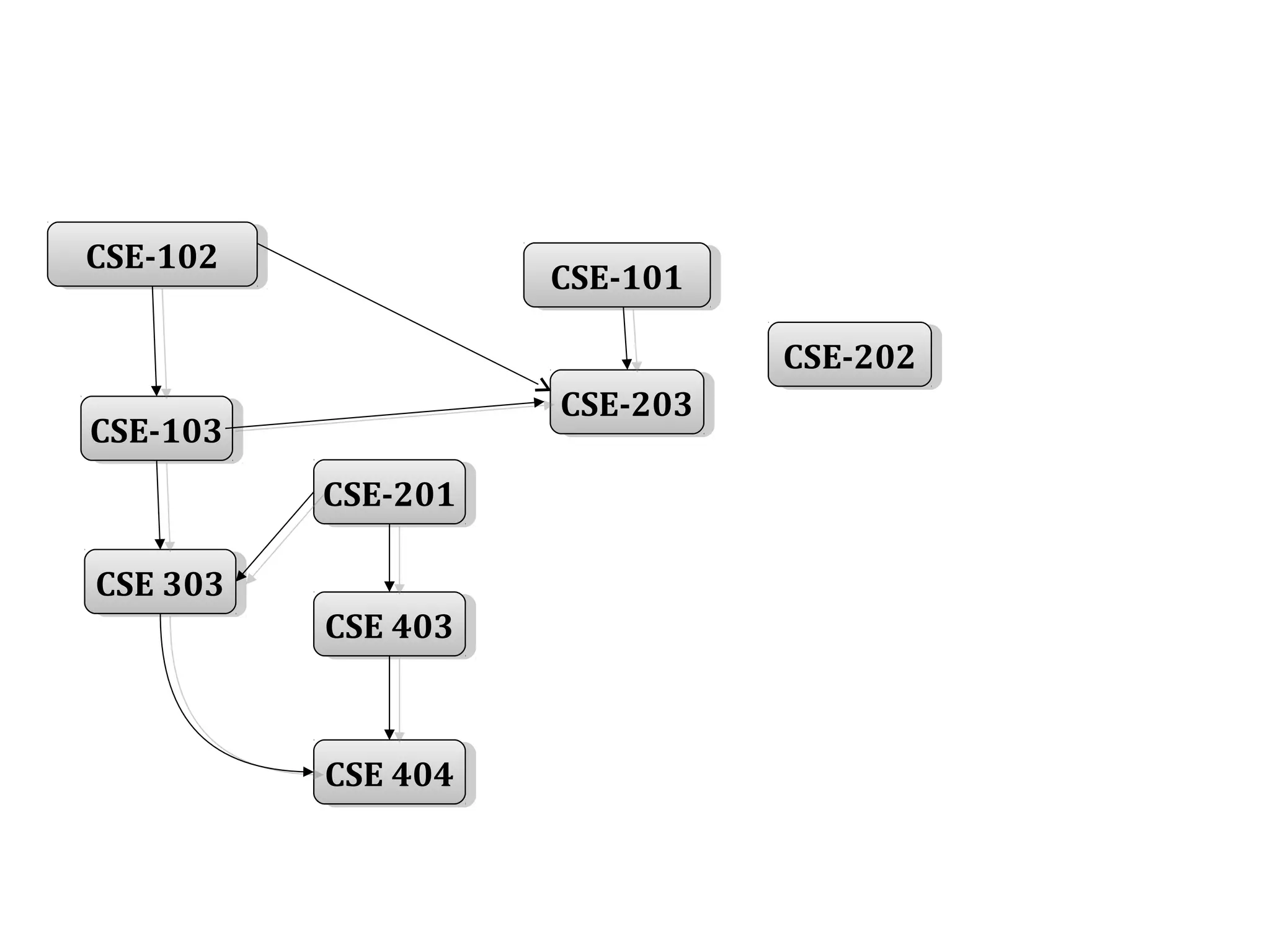
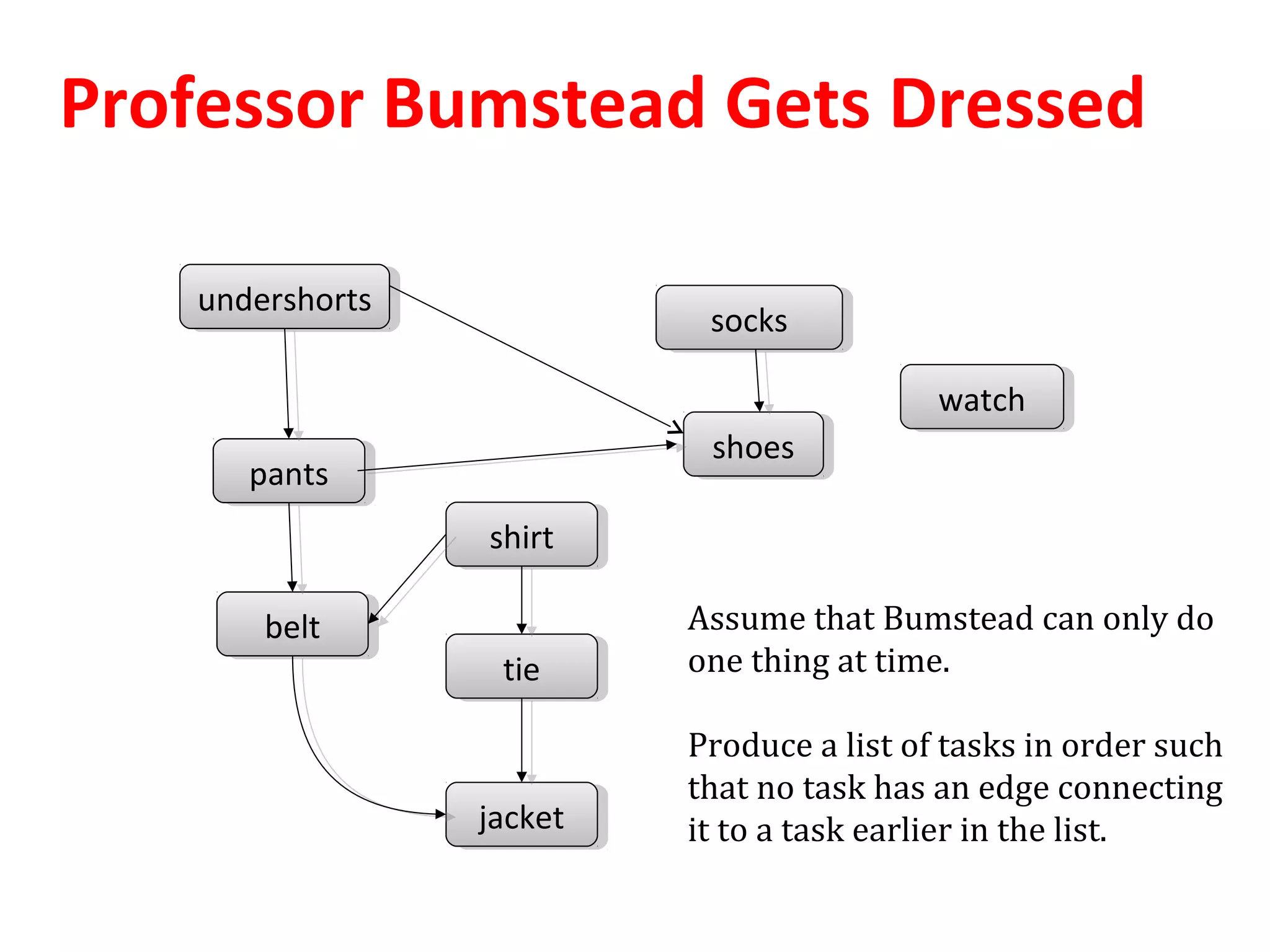
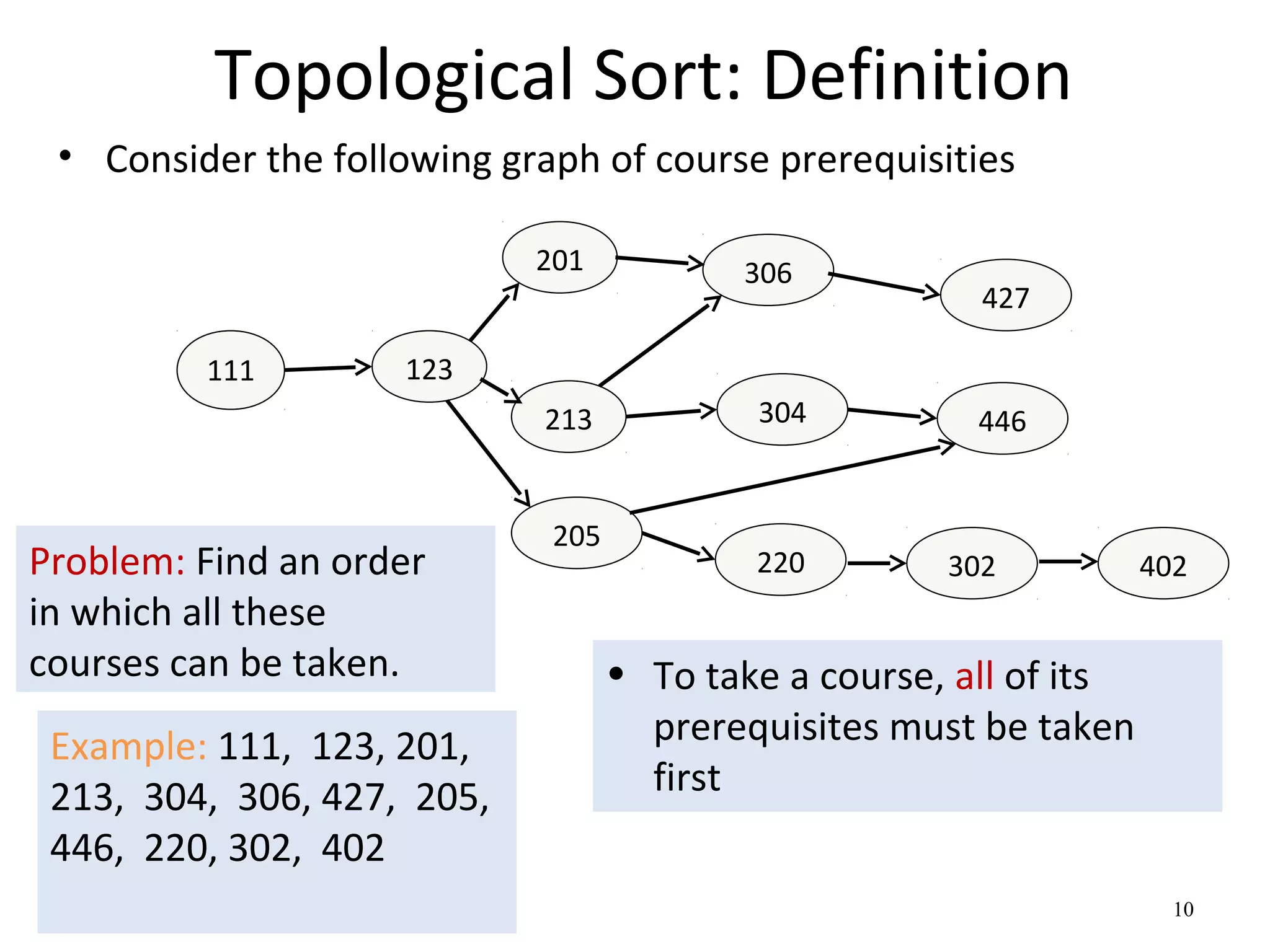
Directed graphs and topological sorting can be used to determine a feasible ordering of courses based on prerequisites. Topological sorting algorithms perform a depth-first search on a directed acyclic graph (DAG) of course prerequisites to output a linear ordering of courses with no edges between earlier and later courses. For example, a topological sorting of computer science courses outputs an order allowing each course to be taken only after completing its prerequisites.

1. Applications of DFS

2. Directed Acyclic Graph
• A directed acyclic graph or DAG is a directed graph with no
directed cycles:

3. Topological Sorting
 Topological sort of a DAG:
 Linear ordering of all vertices in graph G such that
vertex u comes before vertex v if edge (u, v) ∈ G
 Real-world application:
 Scheduling a dependent graph,
 Find a feasible course plan for university studies

4. Topological Sorting
 Assume a directed acyclic graph G = (V,E).
 A topological sort of a DAG G=(V,E) is a linear ordering of all its
vertices such that if G contains an edge (u,v), then u appears
before v in the ordering.
 We can view a topological sort of a graph as an ordering of its
vertices along a horizontal line so that all directed edges go
from left to right.
 If the graph is cyclic, then such ordering is not possible. In
other words the topological sorting can be applied on a
graph if it is directed and acyclic.
 Thus topological sort is different from the usual kind of
"sorting"

5. Topological Sorting
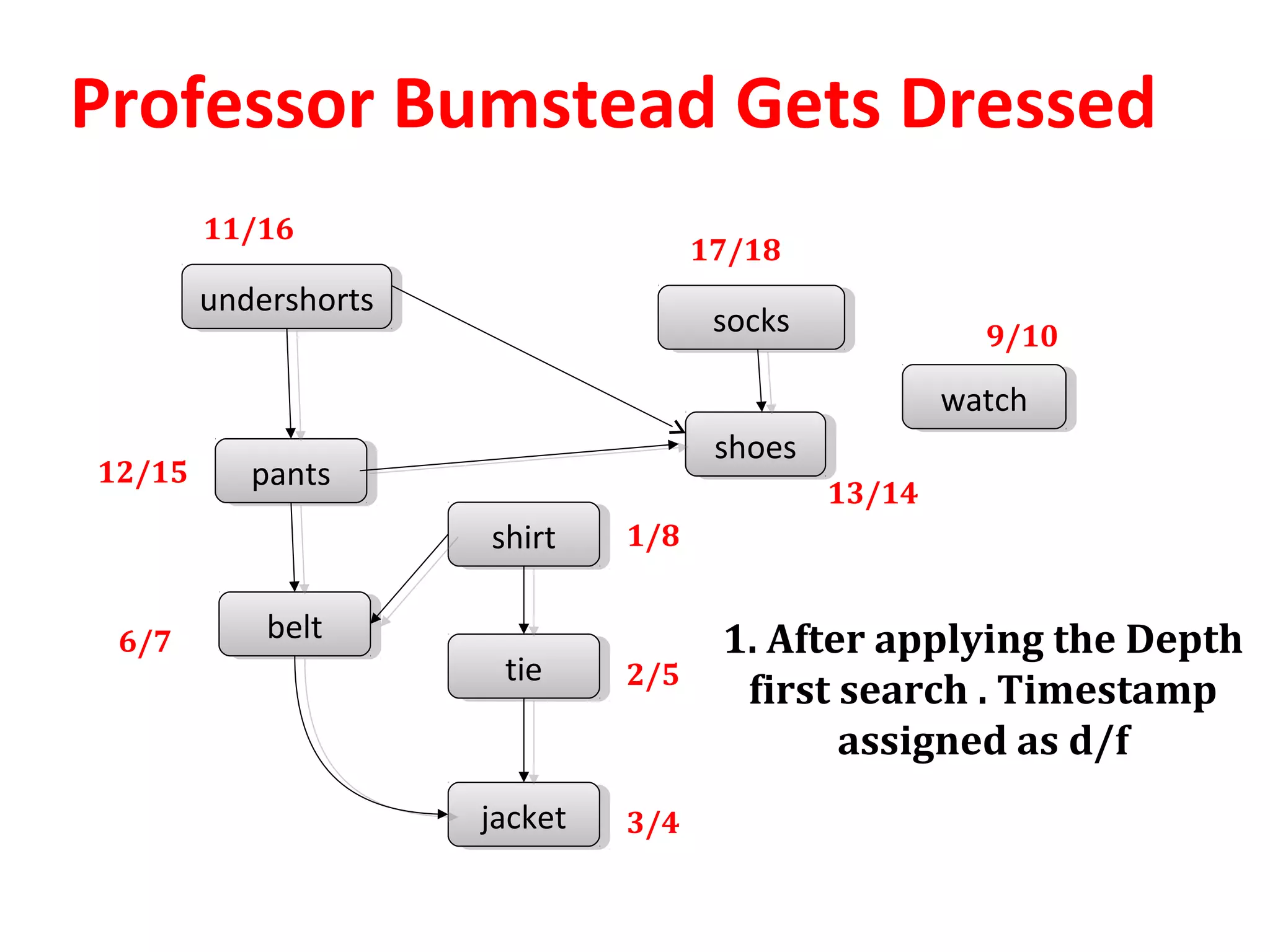
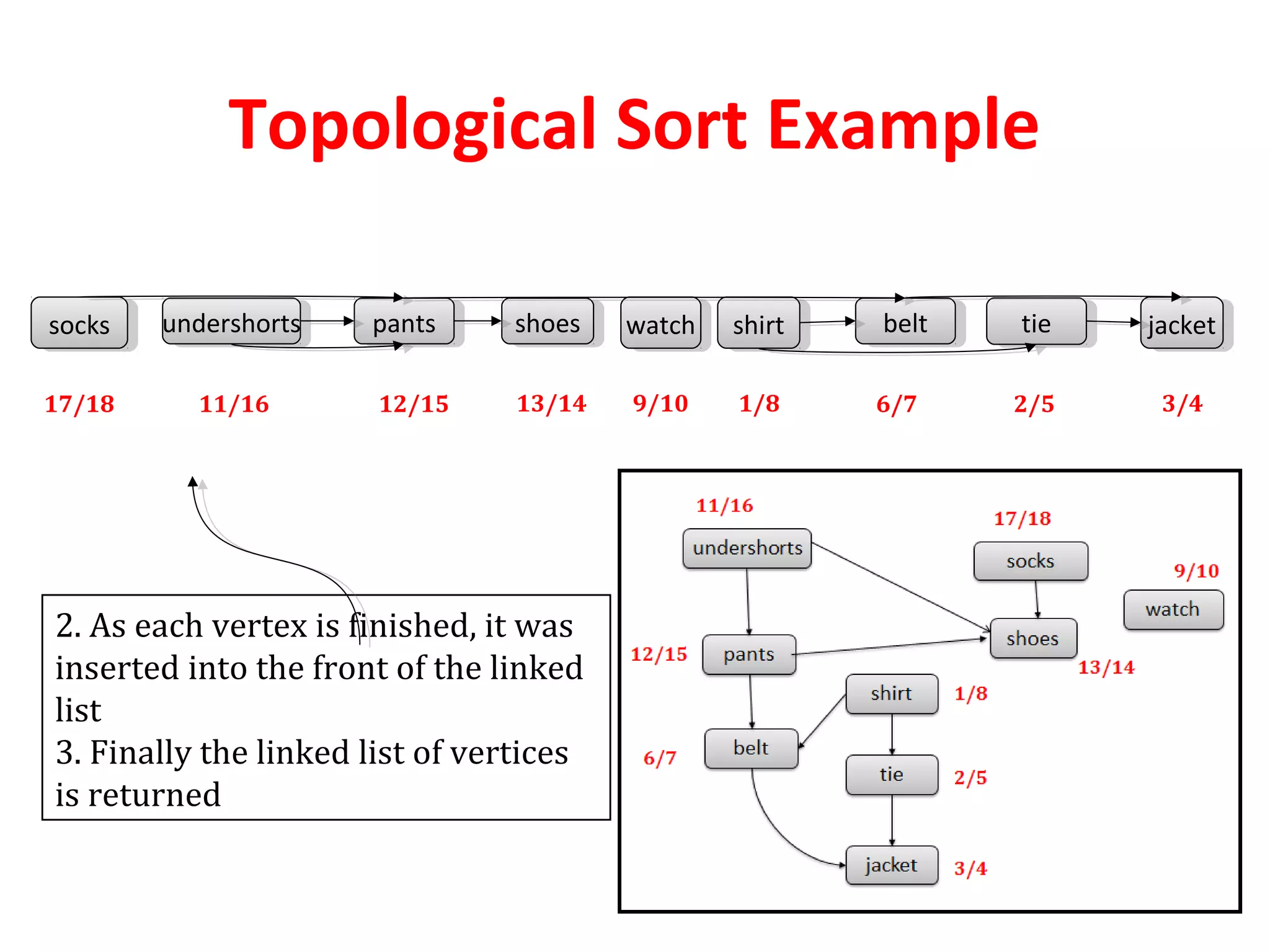
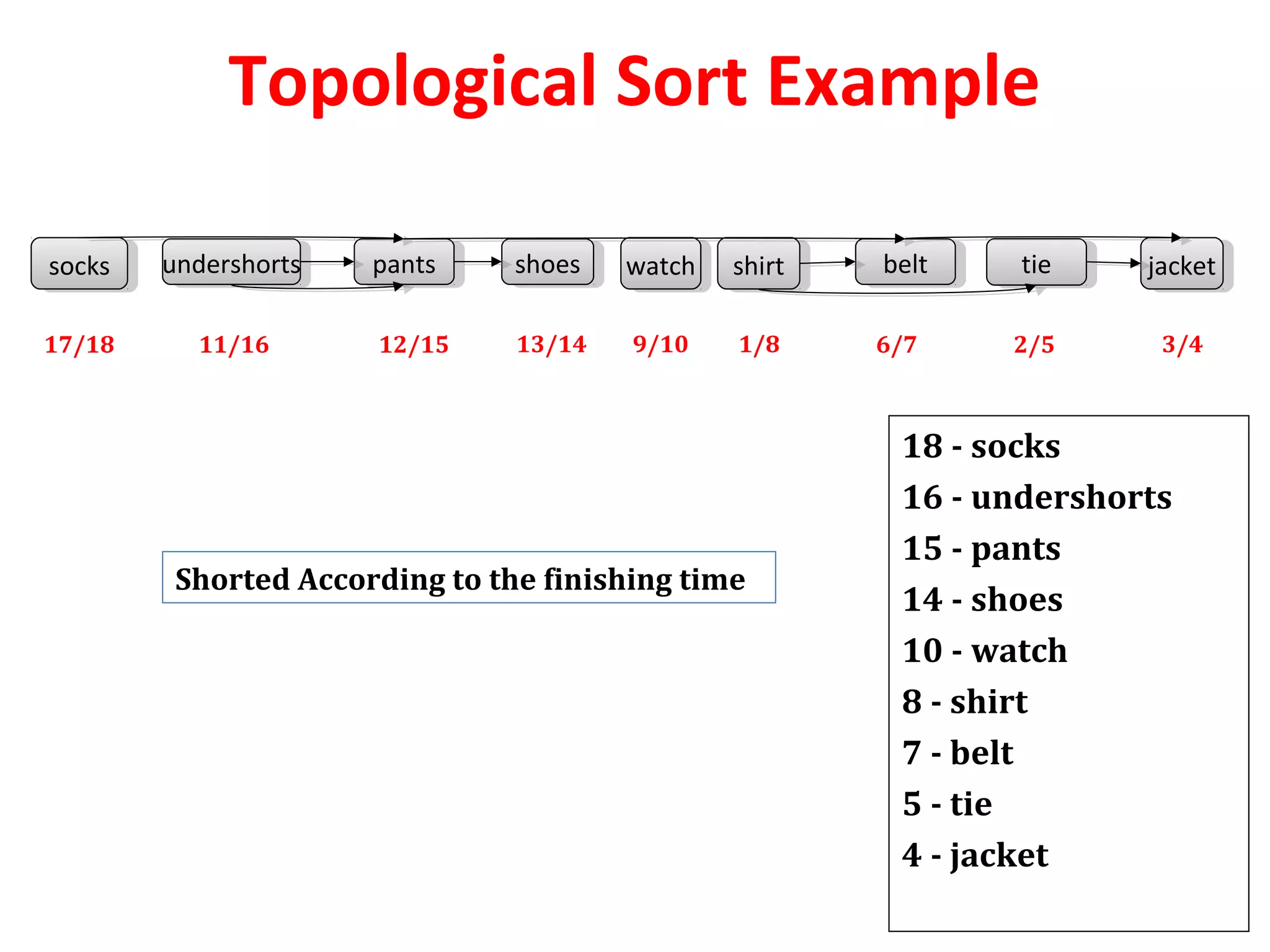
 TOPOLOGICAL-SORT(G)
1. Call DFS(G) to compute finishing time f[v] for
each vertex v.
2. As each vertex is finished, it is inserted into the
front of the linked list.
3. Finally return the linked list of vertices

6. shirtshirt
tietie
jacketjacket
sockssocks
shoesshoes
watchwatch
undershortsundershorts
pantspants
beltbelt Assume that Bumstead can only do
one thing at time.
Produce a list of tasks in order such
that no task has an edge connecting
it to a task earlier in the list.
Professor Bumstead Gets Dressed

7. Professor Bumstead Gets Dressed
shirtshirt
tietie
jacketjacket
sockssocks
shoesshoes
watchwatch
undershortsundershorts
pantspants
beltbelt
11/16
12/15
6/7
17/18
9/10
13/14
1/8
2/5
3/4
1. After applying the Depth
first search . Timestamp
assigned as d/f

8. Topological Sort Example
shirtshirt tietie jacketjacketsockssocks shoesshoes watchwatchundershortsundershorts pantspants beltbelt
17/18 11/16 12/15 13/14 9/10 1/8 6/7 2/5 3/4
2. As each vertex is finished, it was
inserted into the front of the linked
list
3. Finally the linked list of vertices
is returned

9. Topological Sort Example
shirtshirt tietie jacketjacketsockssocks shoesshoes watchwatchundershortsundershorts pantspants beltbelt
17/18 11/16 12/15 13/14 9/10 1/8 6/7 2/5 3/4
18 - socks
16 - undershorts
15 - pants
14 - shoes
10 - watch
8 - shirt
7 - belt
5 - tie
4 - jacket
Shorted According to the finishing time

10. 10
Topological Sort: Definition
• Consider the following graph of course prerequisities
111
201
123
213
205
220 302
304
306
446
427
402Problem: Find an order
in which all these
courses can be taken. • To take a course, all of its
prerequisites must be taken
first
Example: 111, 123, 201,
213, 304, 306, 427, 205,
446, 220, 302, 402

11. Strongly connected components

12. Strongly Connected
• Every pair of vertices are reachable from each other
• Graph G is strongly connected if, for every u and v in V,
there is some path from u to v and some path from v to u.
Strongly
Connected
Not Strongly
Connected
A B
C
D
E
A B
C
E
D

13. Strongly-Connected Components
 A strongly connected component of a graph is a
maximal subset of nodes (along with their
associated edges) that is strongly connected. Nodes
share a strongly connected component if they are
inter-reachable.

14. Strongly Connected Components
a
b
d
c
e
f
g
{ a , c , g }
{ f , d , e , b }

15. Transpose of a Directed Graph
 Transpose of G = (V,E):
GT
=(V, ET
), where ET
={(u, v): (v, u) ∈E}
 If G is a DAG then GT
is also a DAG
 If we print the topological order of G in the reverse
order, then it is a topological order of GT

16. Finding Strongly Connected
Components
• Input: A directed graph G = (V,E)
• Output: a partition of V into disjoint sets so that each
set defines a strongly connected component of G

17. Algorithm
• The intention is to:
1. Perform depth first search and label vertices in
post fix order
2. compute reversed directed graph
3. perform depth first search on reversed graph
4. components of this forest are strongly connected
components

18. Algorithm
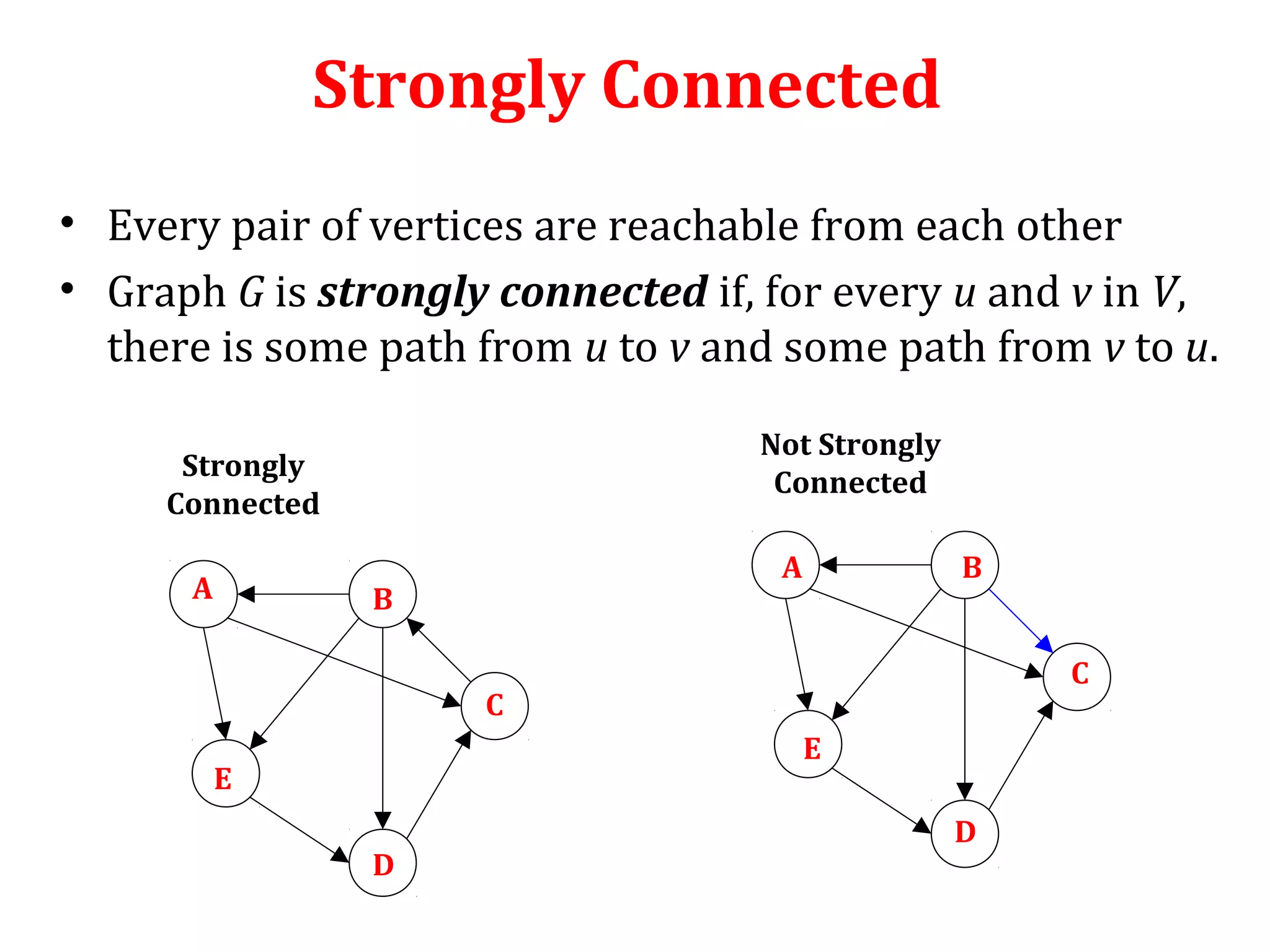
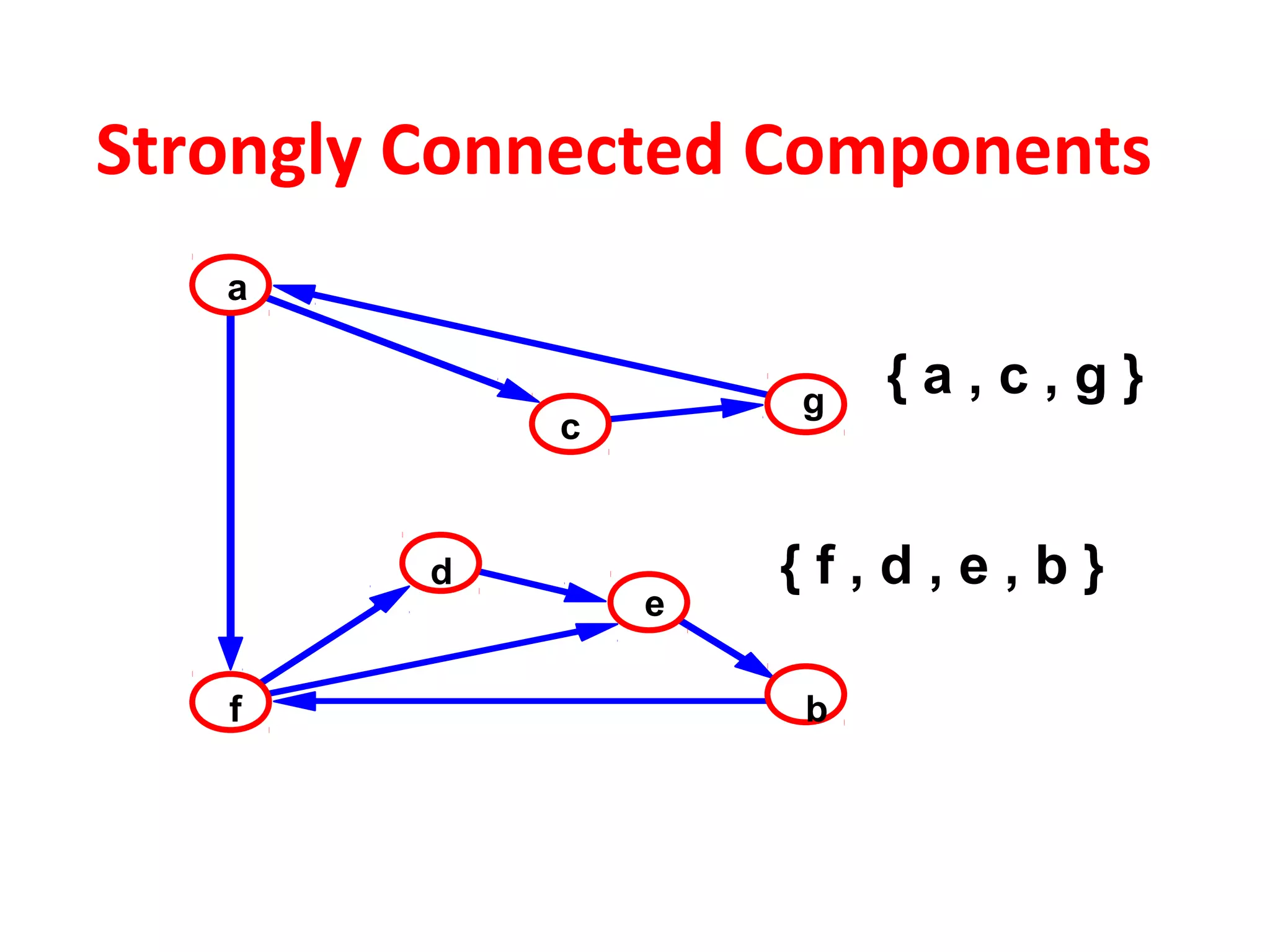
Strongly-Connected-Components(G)
1. Perform depth first search on graph G that is call DFS(G)
to compute finishing times f[u] for each vertex u.
2. Compute reversed directed graph GT
of graph G
3. Perform depth first search on reversed graph that is call
DFS(GT
), but in the main loop of DFS, consider the vertices
in order of decreasing f[u]
4. Output the vertices of each tree in the depth-first forest
of step 3 as a separate strongly connected component.

19. A
d=13
f=14
A
d=13
f=14
B
d=11
f=16
B
d=11
f=16
C
d=1
f=10
C
d=1
f=10
D
d=8
f=9
D
d=8
f=9
E
d=12
f=15
E
d=12
f=15
F
d=3
f=4
F
d=3
f=4
G
d=2
f=7
G
d=2
f=7
H
d=5
f=6
H
d=5
f=6
Strongly-Connected Components
DFS on G, starting at c.

20. A
d=2
f=5
π=B
A
d=2
f=5
π=B
B
d=1
f=6
π=NIL
B
d=1
f=6
π=NIL
C
d=7
f=10
π=NIL
C
d=7
f=10
π=NIL
D
d=8
f=9
π=C
D
d=8
f=9
π=C
E
d=3
f=4
π=A
E
d=3
f=4
π=A
F
d=12
f=13
π=G
F
d=12
f=13
π=G
G
d=11
f=14
π=NIL
G
d=11
f=14
π=NIL
H
d=16
f=15
π=NIL
H
d=16
f=15
π=NIL
DFS on GT

21. A
d=2
f=5
π=B
A
d=2
f=5
π=B
B
d=1
f=6
π=NIL
B
d=1
f=6
π=NIL
C
d=7
f=10
π=NIL
C
d=7
f=10
π=NIL
D
d=8
f=9
π=C
D
d=8
f=9
π=C
E
d=3
f=4
π=A
E
d=3
f=4
π=A
F
d=12
f=13
π=G
F
d=12
f=13
π=G
G
d=11
f=14
π=NIL
G
d=11
f=14
π=NIL
H
d=16
f=15
π=NIL
H
d=16
f=15
π=NIL
DFS on GT
 This is GT
, labeled after running DFS(GT
). but in the main
loop of DFS, the vertices are processed in order of
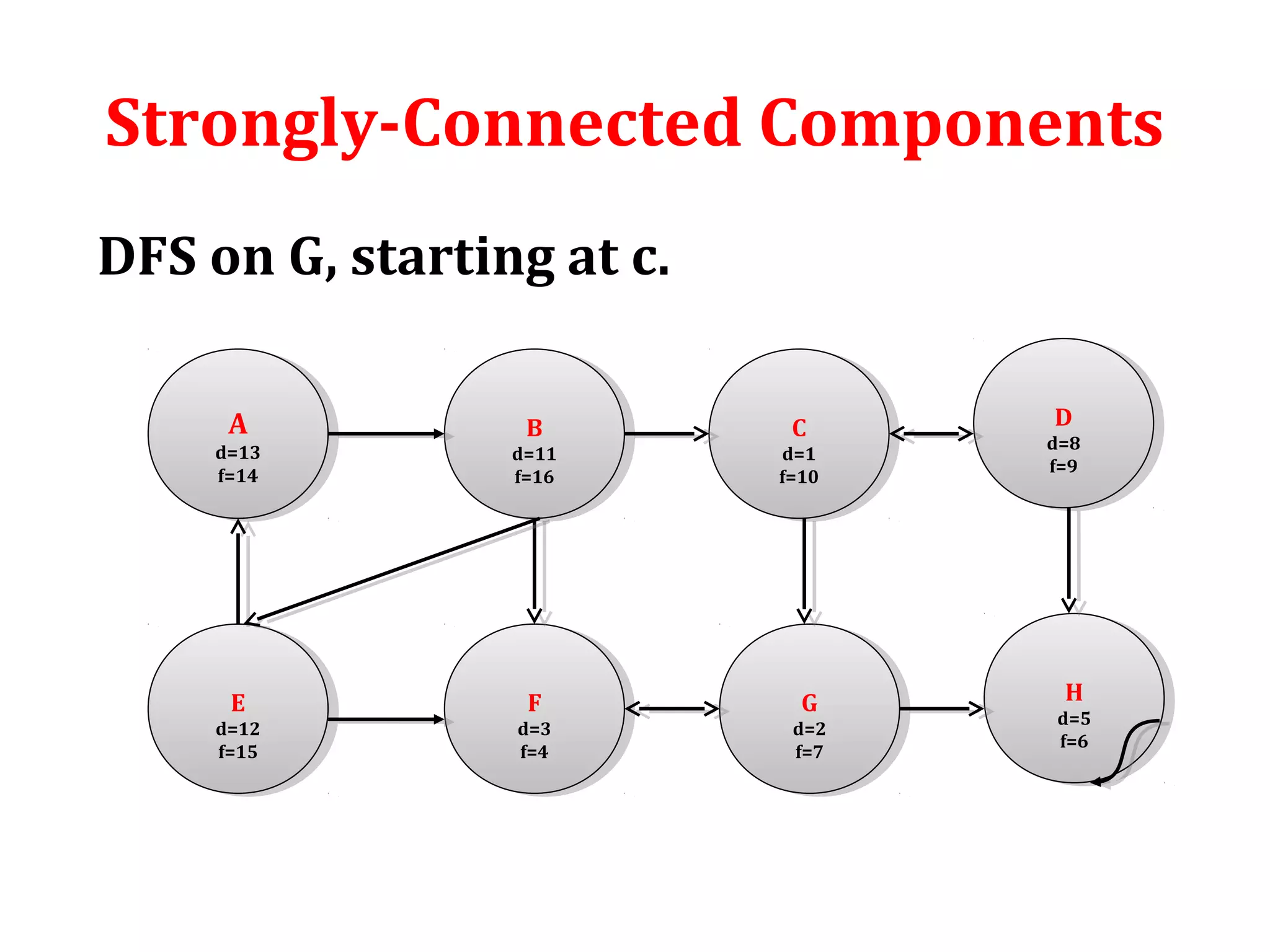
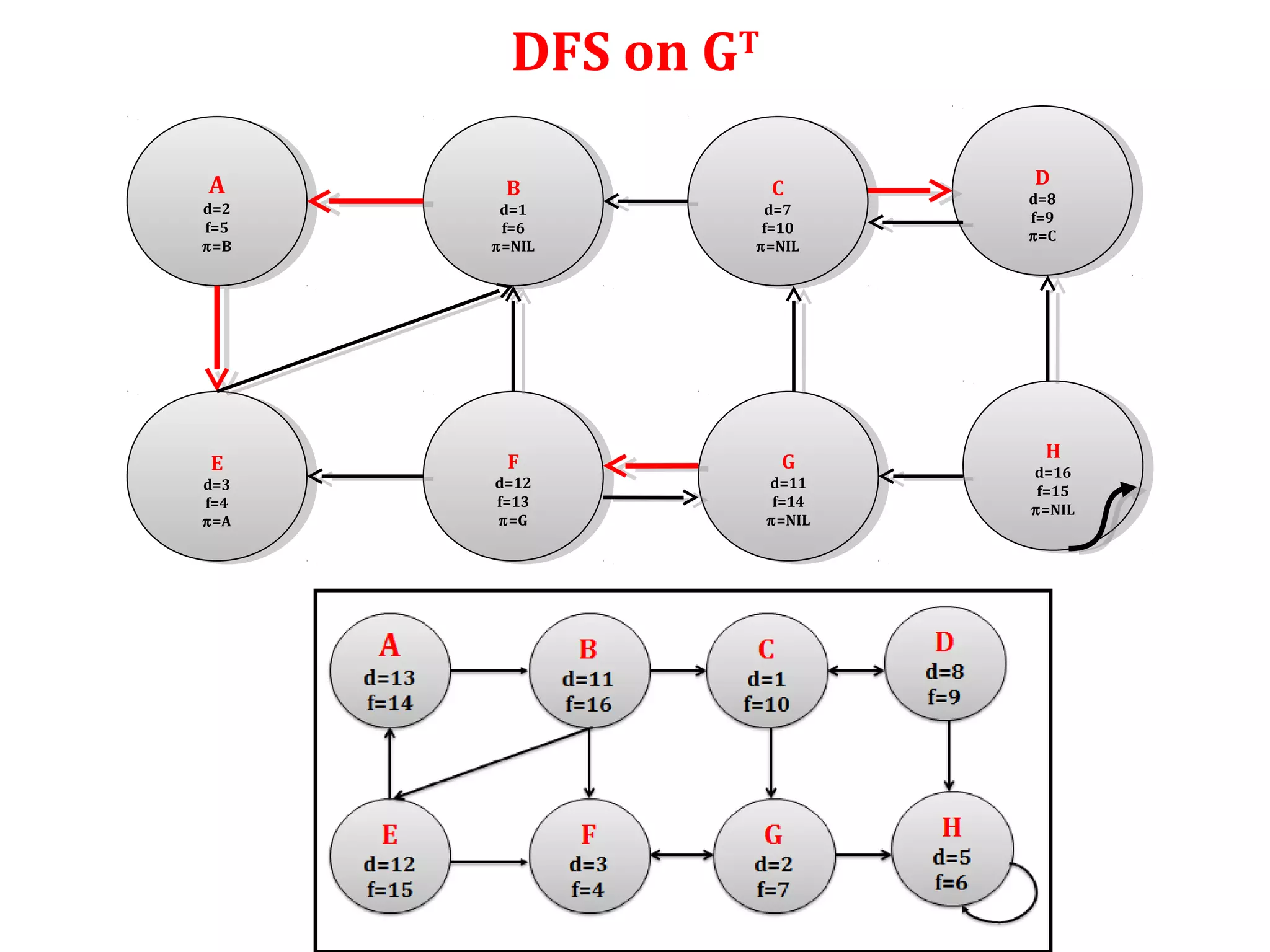
decreasing f[u](from G). That is B E A C D G H F
GT
:

22. Strongly-Connected Components
These are the 4 trees that result, yielding the strongly connected
components.
Finally, merge the nodes of any given tree into a super-node, and
draw links between them, showing the resultant acyclic
component graph.
a
b c
d
e
f
g h
a b c d
e f g h
abe cd
fg h
Component Graph

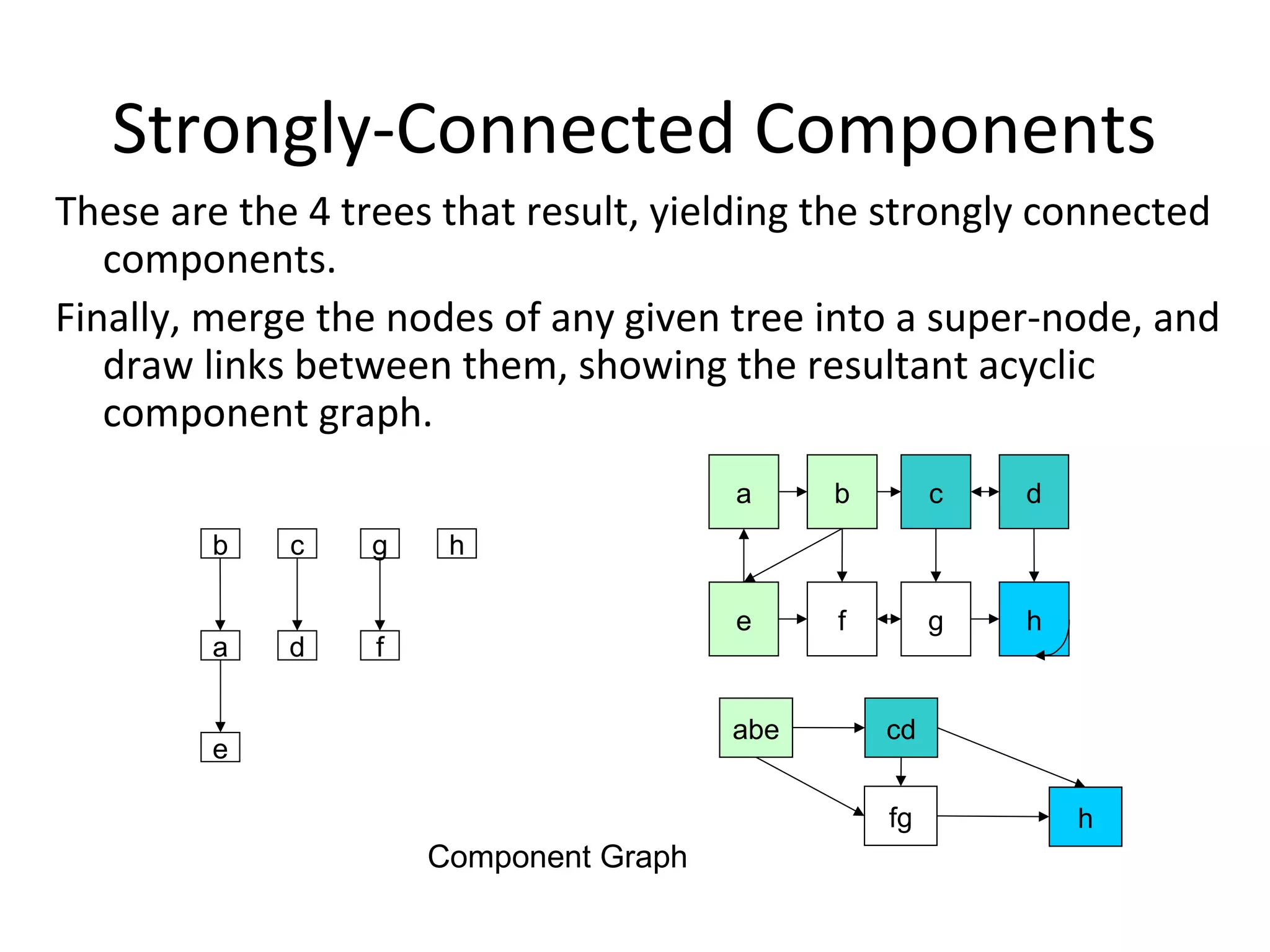
23. Time Complexity Analysis
Strongly-Connected-Components(G)
1. call DFS(G) to compute finishing times f[u] for each vertex u.
Cost: O(E+V)
2. compute GT
Cost: O(E+V)
3. call DFS(GT
), but in the main loop of DFS, consider the vertices in
order of decreasing f[u] Cost: O(E+V)
4. output the vertices of each tree in the depth-first forest of step 3
as a separate strongly connected component.
The graph GT
is the transpose of G, which is visualized by
reversing the arrows on the digraph.
• Cost: O(E+V)

24. Example

25. MD. Shakhawat Hossain
Student of Computer Science & Engineering Dept.
University of Rajshahi

26. CSE-201CSE-201
CSE 403CSE 403
CSE 404CSE 404
CSE-101CSE-101
CSE-203CSE-203
CSE-202CSE-202
CSE-102CSE-102
CSE-103CSE-103
CSE 303CSE 303
Problem: Find an order in which all these
courses can be taken.
• Introduction to Computer → CSE-101
• Mathematics → CSE-102
• Programming with C → CSE-103
• Data Structure → CSE-201
• Algorithm → CSE-202
• OOP → CSE-203
• Compiler Design → CSE 303
• Software Engineering → CSE 403
• Advanced Software Engineering → CSE 403
• Consider the following graph of course prerequisites
• To take a course, all of its prerequisites must be taken first

27. Desired Output
CSE 201CSE 201 CSE 403CSE 403 CSE 404CSE 404CSE-101CSE-101 CSE-203CSE-203 CSE-202CSE-202CSE-102CSE-102 CSE-103CSE-103 CSE 303CSE 303
17/18 11/16 12/15 13/14 9/10 1/8 6/7 2/5 3/4
1. Introduction to Computer → CSE-101
2. Mathematics → CSE-102
3. Programming with C → CSE-103
4. OOP → CSE-203
5. Algorithm → CSE-202
6. Data Structure → CSE-201
7. Compiler Design → CSE 303
8. Software Engineering → CSE 403
9. Advanced Software Engineering → CSE 403

28. CSE-201CSE-201
CSE 403CSE 403
CSE 404CSE 404
CSE-101CSE-101
CSE-203CSE-203
CSE-202CSE-202
CSE-102CSE-102
CSE-103CSE-103
CSE 303CSE 303