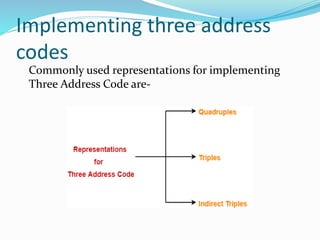
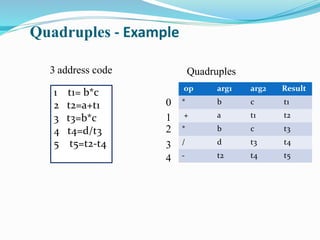
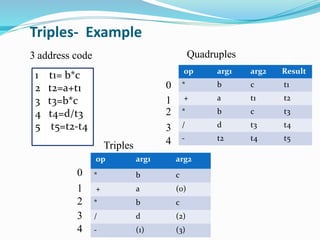
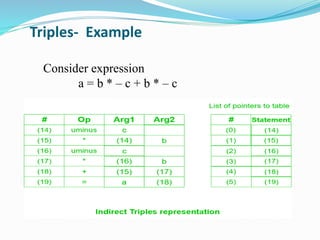
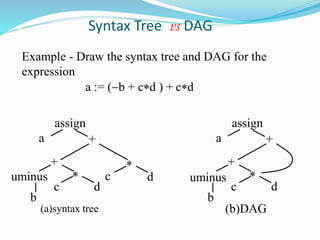
The document discusses different representations of intermediate code in compilers, including high-level and low-level intermediate languages. High-level representations like syntax trees and DAGs depict the structure of the source program, while low-level representations like three-address code are closer to the target machine. Common intermediate code representations discussed are postfix notation, three-address code using quadruples/triples, and syntax trees.

2. Introduction
 Intermediate code is the interface between front end
and back end in a compiler
 Intermediate code is used to translate the source code
into the machine code.

3. Using Intermediate code
 Intermediate code is machine independent, which
makes it easy to retarget the compiler to generate code
for newer and different processors.
 Intermediate code is nearer to the target machine as
compared to the source language so it is easier to
generate the object code.

4. Intermediate Languages
 High Level intermediate code:
This is closer to the source program. It represents the high-
level structure of a program, that is, it depicts the natural
hierarchical structure of the source program. The examples
of this representation are directed acyclic graphs (DAG)
and syntax trees
 Low Level intermediate code
This is closer to the target machine where it represents
the low-level structure of a program. It is appropriate for
machine-dependent tasks like register allocation and
instruction selection. A typical example of this
representation is three-address code.

5. Intermediate code representation
The following are commonly used intermediate code
representation:
 Syntax Tree
 Postfix notation
 Three Address Code

6. Syntax Tree
In syntax tree each internal note represent
operator and leaf node represents operands.
Example:- syntax tree for
a := (b + cd ) + cd
=
a +


+
c d
c duminus
b

7. Example –
x = (a + b * c) / (a – b * c)
Syntax tree

8. Directed Acyclic Graphs for
Expressions
 DAG has leaves corresponding to atomic operands
and interior nodes corresponding to operators.
 The difference is that a node N in a DAG has more
than one parent if N represents a common sub-
expression; in a syntax tree, the tree for the common sub-
expression would be replicated as many times as the sub-
expression appears in the original expression.
.

9. Directed Acyclic Graphs for
Expressions
Example- DAG for the expression
a + a * (b - c) + (b - c) * d

10. assign
a +


b
+
c d
c duminus
assign
a +

b
+
c d
uminus
(a)syntax tree (b)DAG
Syntax Tree vs DAG
Example - Draw the syntax tree and DAG for the
expression
a := (b + cd ) + cd

11. Postfix Notation
Linear representation of syntax tree.
 In postfix notation (also known as reverse polish or suffix
notation), the operator is shifted to the right end, as ab* for the
expression a*b. In postfix notation, parentheses are not required
because the position and the number of arguments of the
operator allow only a single way of decoding the postfix
expression.
The postfix notations can easily be evaluated by using a stack,
and generally the evaluation process scans the postfix code left
to right.

12. Postfix Notation
Example- 1. Given expression
P + (–Q + R * S)
The postfix notation for the given expression is:
PQ - RS * ++
Example 2. Given Expression (l + m) * n
the postfix notation will be l m + n *.
Example 3. Given Expression p * (q + r)
the postfix expression will be p q r + *.
Example 4. Given Expression (p - q) * (r + s) + (p - q)
the postfix expression will be p q - r s + * p q - +.

13. Three address code
 Three-address code is an intermediate code. It is used
by the optimizing compilers.
 In three-address code, the given expression is broken
down into several separate instructions. These
instructions can easily translate into assembly
language.
 Each Three address code instruction has at most three
operands. It is a combination of assignment and a
binary operator.
 In Three address code there is at most one operator on
the right hand side of the instruction.

14. Three address code- Example
Given Expression:
a := (-c * b) + (-c * d)
Three-address code is as follows:
t1 := -c
t2 := b*t1
t3 := -c
t4 := d * t3
t5 := t2 + t4
a := t5

15. Three address code- Example
Given Expression:
-(a * b) + (c + d) – (a + b + c + d)
Three-address code is as follows:
(1) T1 = a *b
(2) T2 = - T1
(3) T3 = c + d
(4) T4 = T2 + T3
(5) T5 = a + b
(6) T6 = T3 + T5
(7) T7 = T4 – T6

16. Three Address Statements
 Assignment statements:
x = y op z
x = op y
 Indexed assignments:
x = y[i], x[i] = y
 Pointer assignments:
x = &y, x = *y
 Copy statements:
x = y
 Unconditional jumps
goto lab
 Conditional jumps:
if x relop y
goto lab
 Function call
param x… call p,
n return y

17. Implementing three address
codes
Commonly used representations for implementing
Three Address Code are-

18. Implementing three address
codes
1. Quadruples-
In quadruples representation, each instruction is splitted
into the following 4 different fields-
op, arg1, arg2, result
Here-
The op field is used for storing the internal code of the
operator.
The arg1 and arg2 fields are used for storing the two
operands used.
The result field is used for storing the result of the
expression.

19. Quadruples - Example
1 t1= b*c
2 t2=a+t1
3 t3=b*c
4 t4=d/t3
5 t5=t2-t4
3 address code
op arg1 arg2 Result
* b c t1
+ a t1 t2
* b c t3
/ d t3 t4
- t2 t4 t5
Quadruples
0
1
2
3
4

20. Triples
 The triples have three fields to implement the three
address code. The field of triples contains the name of
the operator, the first source operand and the second
source operand.
– Statements can be represented by a record with
only three fields: op, arg1, and arg2
– Avoids the need to enter temporary names into
the symbol table
 In triples, the results of respective sub-expressions are
denoted by the position of expression. Triple is
equivalent to DAG while representing expressions.

21. Triples- Example
1 t1= b*c
2 t2=a+t1
3 t3=b*c
4 t4=d/t3
5 t5=t2-t4
3 address code
op arg1 arg2 Result
* b c t1
+ a t1 t2
* b c t3
/ d t3 t4
- t2 t4 t5
Quadruples
0
1
2
3
4
op arg1 arg2
* b c
+ a (0)
* b c
/ d (2)
- (1) (3)
Triples
0
1
2
3
4

22. Indirect Triples-
 This representation is an enhancement over triples
representation.
 It uses an additional instruction array to list the
pointers to the triples in the desired order.
 Thus, instead of position, pointers are used to store
the results.
 It allows the optimizers to easily re-position the sub-
expression for producing the optimized code.

23. Triples- Example
Consider expression
a = b * – c + b * – c

24. Example
 b * minus c + b * minus c
t1 = minus c
t2 = b * t1
t3 = minus c
t4 = b * t3
t5 = t2 + t4
a = t5
Three address code
minus
*
minus c t3
*
+
=
c t1
b t2t1
b t4t3
t2 t5t4
t5 a
arg1 resultarg2op
Quadruples
minus
*
minus c
*
+
=
c
b (0)
b (2)
(1) (3)
a
arg1 arg2op
Triples
(4)
0
1
2
3
4
5
minus
*
minus c
*
+
=
c
b (0)
b (2)
(1) (3)
a
arg1 arg2op
Indirect Triples
(4)
0
1
2
3
4
5
(0)
(1)
(2)
(3)
(4)
(5)
op
35
36
37
38
39
40

25. MULTIPLE-CHOICE QUESTIONS
1. Which of the following is not true for the intermediate
code?
(a) It can be represented as postfix notation.
(b) It can be represented as syntax tree, and or a DAG.
(c) It can be represented as target code.
(d) It can be represented as three-address code,
quadruples, and triples.

26. MULTIPLE-CHOICE QUESTIONS
2 . Which of the following is true for the low-level
representation of intermediate languages?
(a) It requires very few efforts by the source program to
generate the low-level representation.
(b) It is appropriate for machine-dependent tasks like
register allocation and instruction selection.
(c) It does not depict the natural hierarchical structure
of the source program.
(d) All of these

27. MULTIPLE-CHOICE QUESTIONS
3.Which of the following is true for intermediate code
generation?
(a) It is machine dependent.
(b) It is nearer to the target machine.
(c) Both (a) and (b)
(d) None of these

28. MULTIPLE-CHOICE QUESTIONS
4. The reverse polish notation or suffix notation is also
known as _________ .
(a) Infix notation
(b) Prefix notation
(c) Postfix notation
(d) None of above