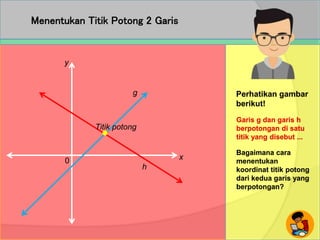
Dokumen ini berisi petunjuk penggunaan CD pembelajaran interaktif yang berisi pertanyaan-pertanyaan kognitif untuk membantu peserta didik mencapai tujuan pembelajaran. CD ini efektif jika digunakan secara tepat dengan mengklik untuk memunculkan pertanyaan dan informasi berikutnya setelah peserta didik menjawab dengan benar.

1. © 2018
PPG Dalam Jabatan UPGRIS
Tahap 1 Tahun 2018

2. PETUNJUK
CD Pembelajaran ini
memuat serangkaian per-
tanyaan kognitif (good
questions). Peserta didik
dapat mencapai tujuan
pembelajaran dengan
mudah dengan cara
menjawab semua
pertanyaan tersebut. CD
pembelajaran ini efektif
apabila digunakan secara
tepat
Adapun caranya adalah:
1. Klik, untuk memunculkan
informasi / pertanyaan
2. Klik berikutnya setelah
peserta didik menjawab
pertanyaan dengan benar
(beri kesempatan berpikir,
jangan klik sebelum peserta
didik menjawab)
3. Begitu seterusnya sampai
peserta didik menemukan
simpulan

3. Menentukan Titik Potong 2 Garis
Hi!
Sb. x
Sb. y

4. Menentukan Titik Potong 2 Garis
Kompetensi Dasar :
3.4 Menganalisis fungsi linear (sebagai persamaan garis lurus)
dan menginterpretasikan grafiknya yang dihubungkan dengan
masalah kontekstual
4.4 Menyelesaikan masalah kontekstual yang berkaitan dengan
fungsi linear sebagai persamaan garis lurus
Indikator Pencapaian Kompetensi :
3.4.5 Menentukan titik potong dua garis
4.4.5 Memecahkan masalah yang berkaitan dengan titik potong
dua garis
Oke, hari ini
kita belajar
tentang ....

5. Materi Prasyarat
Coba tentukan
gradien (m) dari
persamaan garis
berikut!
y = 4x + 5 m = 4
y = -x + 3 m = -1
y + 2x = 3, m = ?
y = -2x + 3
m = -2
3y + 2x = 6, m = ?
3y = -2x + 6
m =
−𝟐
𝟑
y =
−𝟐
𝟑
𝒙 +
𝟔
𝟑

6. Materi Prasyarat
Bagaimanakah
gradien dua garis
yang saling sejajar?
Misal
𝒎 𝟏 = gradien garis pertama
𝒎 𝟐 = gradien garis kedua
Gradien dua garis yang
saling sejajarBagaimanakah
gradien dua garis
yang saling tegak
lurus?
𝒎 𝟏 = 𝒎 𝟐
Gradien dua garis yang
saling tegak lurus
𝒎 𝟏 x 𝒎 𝟐= -1

7. Materi Prasyarat
Tentukan Gradien
garis yang sejajar
dengan gradien
garis berikut!
y = 3x + 5
𝒎 𝟏 = 3
y = -x + 5
𝒎 𝟏 =-1 𝒎 𝟐=-1
𝒎 𝟐 = 3

8. Materi Prasyarat
Tentukan Gradien
garis yang tegak
lurus dengan
gradien garis
berikut!
y = 3x + 5
𝒎 𝟏 = 3
y = -x + 5
𝒎 𝟏 = -1 𝒎 𝟐=1
𝒎 𝟐 = −
𝟏
𝟑

9. Materi Prasyarat
y - 𝒚 𝟏 = m(x - 𝒙 𝟏)
Persamaan Garis Lurus yang melalui (𝒙 𝟏, 𝒚 𝟏) dan
bergradien m dapat ditentukan dengan rumus :

10. Menentukan Titik Potong 2 Garis
0 x
y
Titik potong
g
h
Perhatikan gambar
berikut!
Garis g dan garis h
berpotongan di satu
titik yang disebut ...
Bagaimana cara
menentukan
koordinat titik potong
dari kedua garis yang
berpotongan?

11. Menentukan Titik Potong 2 Garis
Perhatikan contoh
berikut!
Tentukan titik potong dari garis dengan persamaan
y = x – 5 dan y = 4x + 10 !
Selesaian :
Subtitusikan y = x – 5 ke persamaan y = 4x + 10,
sehingga diperoleh :
Untuk memperoleh nilai y,
substitusikan x = -5 ke
salah satu persamaan.
Pilih y = x – 5 sehingga
diperoleh :
Jadi, koordinat titik
potongnya (-5,-10)
x – 5 = 4x + 10
⇔ x – 4x = 5 + 10
⇔ -3x = 15
⇔ x =
𝟏𝟓
−𝟑
⇔ x = -5
y = -5 – 5
⇔ y = -10

12. Menentukan Titik Potong 2 Garis
Perhatikan contoh
berikut!
Tentukan titik potong dari garis dengan persamaan
4y + x = 8 dan 3y + 2x – 6 = 0!
Selesaian :
4y + x = 8 diubah ke bentuk
Jadi, koordinat titik
potongnya (0,2)
x = -4y + 8
⇔ 3y – 8y + 16 – 6 = 0
Substitusikan x = -4y + 8
ke persamaan 3y + 2x – 6 = 0
3y + 2(-4y + 8) – 6 = 0
⇔ -5y + 10= 0
⇔ -5y = -10
⇔ y =
−𝟏𝟎
−𝟓
⇔ y = 2
Substitusikan y = 2
ke salah satu
persamaan 4y + x =
8
Diperoleh
4(2) + x = 8
⇔ 8 + x = 8
⇔ x = 0

13. Menentukan Titik Potong 2 Garis
Perhatikan contoh
berikut!
Tentukan Persamaan Garis yang melalui titik
potong dari 4y + x = 8 dan 3y + 2x – 6 = 0 dan tegak
lurus y = 4x + 6 !
Selesaian :
Pada contoh sebelumnya,
diperoleh
Jadi, persamaan garis yang dimaksud y = −
𝟏
𝟒
𝐱 + 𝟐
Sehingga x1 = 0, y1 = 2
Koordinat titik potong 4y + x =
8 dan 3y + 2x – 6 = 0 adalah
(0,2)
Gradien y = 4x + 6 adalah
m1 = 4
y - 𝒚 𝟏 = m2(x - 𝒙 𝟏)
⇔ y - 𝟐 = −
𝟏
𝟒
(x - 𝟎)
⇔ y - 𝟐 = −
𝟏
𝟒
𝐱
Karena tegak lurus maka
⇔ y = −
𝟏
𝟒
𝐱 + 𝟐
m2 = −
𝟏
𝟒

14. Mari Bermain !
Ikuti aturan
berikut !
Ada 9 soal yang akan ditayangkan secara acak satu
persatu.
Setiap soal yang ditayangkan harus dijawab oleh
masing-masing kelompok
Jawaban diisikan pada kotak sesuai dengan nomor
yang disebutkan, jika benar dibubuhi tanda centang
(v) kalau salah (x)
Kelompok yang sudah mendapat tanda (v) harus
berteriak “hore!”
Nilai diperoleh dari jawaban benar.
Jaga kejujuran dan sportivitas

15. Course Review Horray
1
987
654
2 3

16. © 2018
Penyusun
Muhamad Husni Mubaraq, S.Pd.
Guru Matematika SMP Al Musyaffa’ Kendal