Dokumen tersebut membahas berbagai jenis fungsi matematika beserta definisinya, contohnya, daerah asal dan hasil, serta grafiknya. Jenis-jenis fungsi yang dijelaskan antara lain fungsi linear, polinomial, pangkat, akar, trigonometri, logaritma, dan lain-lain.

1. 2.1 Fungsi
Secara intuitif, kita pandang y sebagai fungsi dari x jika terdapat
aturan dimana nilai y (tunggal) mengkait nilai x.
Contoh: 1. a. b.
Definisi:
Suatu fungsi adalah suatu himpunan pasangan terurut (x,y) dimana
himpunan semua nilai x disebut daerah asal (domain ) dan himpunan
semua nilai y = f(x) disebut daerah hasil (ko-domain) dari fungsi
BAB 2. FUNGSI & GRAFIKNYA
y = f(x)x
f
2
2 5y x
2
9y x
A B
Notasi: f : A →B
1
Daerah hasilDaerah asal
Untuk contoh 1.a. mendefinisikan suatu fungsi. Namakan fungsi
itu f. Fungsi f adalah himpunan pasangan terurut (x,y) sehingga x
dan y memenuhi:
Fungsi f ini memuat pasangan terurut (0,5);(1,7);(-1,7);
(2,13);(-2,13);(10,205)
Dan f memuat tak berhingga banyak pasangan terurut.
2
{( , )/ 2 5}f x y x
x 0 1 -1 2 -2 … 10
y 5 7 7 13 13 205

2. x
y
y = f(x)
Wf
y
Catatan:
1. Himpunan A, B є
2. Fungsi: y = f(x) ,
x peubah bebas
y peubah tak bebas, bergantung pada x
3. Daerah asal fungsi: Df = A = {x | fungsi f terdefinisi}
4. Daerah hasil fungsi: Wf = {y є B | y = f(x), x є Df }
5. Grafik fungsi: {(x,y) | x є Df , y = f(x)) }
2
x
Df
x
Soal:
Buatlah sketsa grafik fungsi berikut, kemudian
tentukan daerah asal dan dan daerah hasilnya.
a. y = 2x + 1 b. y = x2 - 1
Ada beberapa penyajian fungsi yaitu
a. Secara verbal : dengan uraian kata-kata.
b. Secara numerik : dengan tabel
c. Secara visual : dengan grafik
d. Secara aljabar : dengan aturan/rumusan eksplisit

3. Contoh:
1. Secara verbal
Biaya pengiriman surat tercatat seberat w ons adalah B(w).
Aturan yang digunakan Kantor Pos adalah sebagai berikut.
Biaya pengiriman adalah Rp 1.000,00 untuk berat sampai
satu ons, ditambah Rp 250,00 untuk setiap ons tambahan
sampai 5 ons.
2. Secara numerik
Biaya pengiriman surat tercatat ditunjukkan tabel berikut.
Berat w (ons) Biaya B(w) (rupiah)
0 < w ≤ 1 1.000
1< w ≤ 2 1.250
2 < w ≤ 3 1.500
3 < w ≤ 4 1.750
3
3 < w ≤ 4 1.750
4 < w ≤ 5 2.000
3. Secara visual
Biaya pengiriman surat tercatat ditunjukkan grafik berikut.
0 1 2 3 4 5
1.000
1.500
2.000
w
B
Ons
R
u
p
i
a
h

4. 4. Secara aljabar
Biaya pengiriman surat tercatat dinyatakan oleh fungsi
berikut.
1.000, jika 0 1
1.250, jika 1 2
( ) 1.500, jika 2 3
1.750, jika 3 4
2.000, jika 4 5
w
w
B w w
w
w
2.2 Jenis-jenis Fungsi
1. Fungsi linear
Bentuk umum: y = f(x) = ax + b, a dan b konstanta
a = kemiringan garis
b = perpotongan garis dengan sumbu-y
Daerah asal dan daerah hasil: Df = , Wf =
Grafik: y
4
2.2 Jenis-jenis Fungsi
1. Fungsi linear
Bentuk umum: y = f(x) = ax + b, a dan b konstanta
a = kemiringan garis
b = perpotongan garis dengan sumbu-y
Daerah asal dan daerah hasil: Df = , Wf =
Grafik: y
x
b
y = ax + b
2. Polinomial
Bentuk umum:
y = P(x) = an xn + an-1 xn-1 + … + a2 x2 + a1 x + a0
dimana: an, an-1, …, a1, a0 = konstanta,
n = derajat polinom ( an 0)
Daerah asal: Df =

5. Grafik:
Polinom derajat 2: y = P(x) = ax2 + bx + c,
D = b2 - 4ac
x
y
c
a < 0, D > 0
a < 0, D = 0 a < 0, D < 0
y = P(x)
y
c y = P(x)
y
c y = P(x)
x x
x
y
c
a > 0, D > 0 a > 0, D = 0 a > 0, D < 0
y = P(x)
y
c
y = P(x)
y
c
y = P(x)
x x
Soal :
Tentukan daerah asal dan daerah hasil dari fungsi berikut.
a. y = x2 + 2x - 1 b. y = -2x2 + 2x - 4
5
Soal :
Tentukan daerah asal dan daerah hasil dari fungsi berikut.
a. y = x2 + 2x - 1 b. y = -2x2 + 2x - 4
3. Fungsi pangkat
Bentuk umum: y = f(x) = xn , n є
Daerah asal: Df =
Grafik:
y
y = x
y
y = x2
0 0
xx
y
y = x3
0
x

6. 4. Fungsi akar
Bentuk Umum:
Daerah asal dan daerah hasil:
Df = [0,∞), Wf = [0, ∞), jika n genap
Df = , Wf = , jika n ganjil
Grafik:
( ) , 2,3,4,...n
y f x x n
y
0
x
y
0
x
2
y x 3
y x
Soal :
Tentukan daerah asal dan daerah hasil dari fungsi berikut
a. b.1y x 2
2 2y x x
6
Soal :
Tentukan daerah asal dan daerah hasil dari fungsi berikut
a. b.1y x 2
2 2y x x
1
y
x
1
, 0y x
x
y
0 x
5. Fungsi kebalikan
Bentuk umum:
Daerah asal dan daerah hasil: Df = - {0}, Wf = - {0}
Grafik:

7. 6. Fungsi rasional
Bentuk umum: dimana: P, Q adalah polinom
Daerah asal: Df = - { x | Q(x) = 0}
Contoh:
Tentukan daerah asal dari fungsi rasional berikut
a. b.
( )
( )
P x
y
Q x
1
1
x
y
x 2
2
1
x
y
x
7. Fungsi aljabar
Definisi:
Fungsi f disebut fungsi aljabar jika fungsi tersebut dapat
dibuat dengan menggunakan operasi aljabar, yaitu:
penambahan, pengurangan, perkalian, pembagian dan
penarikan akar, yang dimulai dengan polinom.
Contoh:
a. b.
Catatan:
Fungsi linear, polinom, fungsi pangkat, fungsi akar, fungsi
balikan dan fungsi rasional adalah fungsi aljabar.
7
7. Fungsi aljabar
Definisi:
Fungsi f disebut fungsi aljabar jika fungsi tersebut dapat
dibuat dengan menggunakan operasi aljabar, yaitu:
penambahan, pengurangan, perkalian, pembagian dan
penarikan akar, yang dimulai dengan polinom.
Contoh:
a. b.
Catatan:
Fungsi linear, polinom, fungsi pangkat, fungsi akar, fungsi
balikan dan fungsi rasional adalah fungsi aljabar.
1
( )
1
x
f x
x
3
2
2
( ) ( 2) 1
1
x
f x x x
x

8. 8. Fungsi trigonometri
8.1 Fungsi sinus
Bentuk umum: y = f(x) = sin x, x dalam radian
Daerah asal dan daerah hasil: Df = , Wf = [-1,1]
Grafik:
0-π
-1
1
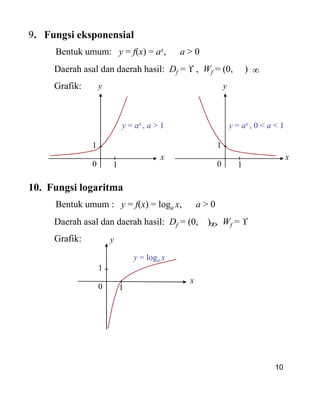
x
y
y = sin x
8.2 Fungsi cosinus
Bentuk umum: y = f(x) = cos x, x dalam radian
Daerah asal dan daerah hasil: Df = , Wf = [-1,1]
Grafik: y
-2π 2ππ
8
8.2 Fungsi cosinus
Bentuk umum: y = f(x) = cos x, x dalam radian
Daerah asal dan daerah hasil: Df = , Wf = [-1,1]
Grafik:
0
-1
1
y
y = cos x
x
-2π
-π π
2π
8.3 Fungsi tangen
Bentuk umum:
Daerah asal : Df = - {π/2 + nπ | n є }
Daerah hasil: Wf =
sin
( ) tan , dalam radian
cos
x
y f x x x
x

9. Grafik:
0-
-1
1
x
y
y = tan x
8.4 Fungsi trigonometri lainnya
Bentuk umum:
-π π 2π-2π
9
8.4 Fungsi trigonometri lainnya
Bentuk umum:
1
( ) sec , dalam radian
cos
1
( ) cosec , dalam radian
sin
1
(
a.
b.
c. ) cot , dalam radian
tan
y f x x x
x
y f x x x
x
y f x x x
x
8.5 Beberapa sifat fungsi trigonometri
a. -1≤ sin x ≤ 1 b. -1 ≤ cos x ≤ 1
c. sin x = sin (x + 2π) d. cos x = cos (x + 2 π)
e. tan x = tan (x + π)

10. x
y
0 1
1
y = ax , a > 1
x
y
0 1
1
y = ax , 0 < a < 1
10. Fungsi logaritma
Bentuk umum : y = f(x) = loga x, a > 0
Daerah asal dan daerah hasil: Df = (0, ) , Wf =
Grafik:
9. Fungsi eksponensial
Bentuk umum: y = f(x) = ax, a > 0
Daerah asal dan daerah hasil: Df = , Wf = (0, )
Grafik:
10
10. Fungsi logaritma
Bentuk umum : y = f(x) = loga x, a > 0
Daerah asal dan daerah hasil: Df = (0, ) , Wf =
Grafik: y
0 1
1
y = loga x
x

11. Contoh:
Golongkan fungsi-fungsi berikut berdasarkan jenisnya.
11. Fungsi transenden
Definisi:
Fungsi transenden adalah fungsi yang bukan fungsi aljabar.
Himpunan fungsi transenden mencakup fungsi trigonometri
invers trigonometri, eksponensial dan logaritma.
4
2
10
5 2 10 10
2
( ) 1 ( ) tan 2
6
( ) 10 ( )
6
( ) log ( )
2
log
1. 2.
3. 4.
5. 6.
( ) 27. . ( )8
2
x
f x x f x x
x
f x f x
x
x
f x x f x x
x
x
f x t t f x x
x x
11
4
2
10
5 2 10 10
2
( ) 1 ( ) tan 2
6
( ) 10 ( )
6
( ) log ( )
2
log
1. 2.
3. 4.
5. 6.
( ) 27. . ( )8
2
x
f x x f x x
x
f x f x
x
x
f x x f x x
x
x
f x t t f x x
x x
12. Fungsi yang terdefinisi secara sepotong-sepotong
(piecewise function)
Definisi:
Fungsi yang terdefinisi secara sepotong-sepotong adalah
fungsi dengan banyak aturan, dimana setiap aturan berlaku
pada bagian tertentu dari daerah asal.
Contoh:
0
( ) | |
0
1.
x x
f x x
x x
y
0 1
1
y = |x|
x
-1

12. 0 1
( ) 2 1 2
0
2.
2
x x
f x x x
x
y
0 1
y = f(x)
x
2
3. Definisikan x = bilangan bulat terbesar yang lebih kecil
atau sama dengan x.
f(x) = x
=
0 0 1
1 1 2
2 2 3
3 3 4
x
x
x
x
0 1 2 3
1
2
3
x
y
4
y = f(x)
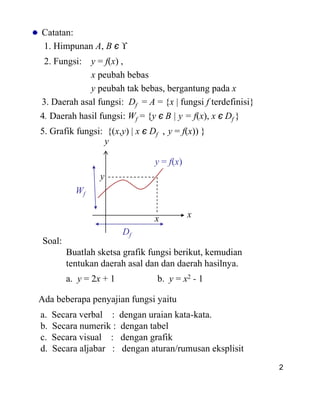
Catatan:
1. f(x) = |x| , f disebut fungsi nilai mutlak
2. f(x) = x , f disebut fungsi bilangan bulat terbesar
12
Catatan:
1. f(x) = |x| , f disebut fungsi nilai mutlak
2. f(x) = x , f disebut fungsi bilangan bulat terbesar
13. Fungsi genap dan fungsi ganjil
Definisi: [Fungsi genap]
Jika fungsi f memenuhi f(-x) = f(x) untuk setiap x di dalam
daerah asalnya, maka f disebut fungsi genap.
x
y
f(x)
-x
x
y = f(x)
Catatan:
Grafik fungsi genap simetri terhadap sumbu-y.

13. Definisi: [Fungsi ganjil]
Jika fungsi f memenuhi f(-x) = -f(x) untuk setiap x di dalam
daerah asalnya, maka f disebut fungsi ganjil.
Catatan: Grafik fungsi ganjil simetri terhadap titik asal.
x
y
f(x)
-x
x
y = f(x)
-f(x)
Soal:
Periksa apakah fungsi berikut adalah fungsi genap atau fungsi
ganjil atau bukan kedua-duanya.
a. f(x) = 1 - x4 b. f(x) = x + sin x
c. f(x) = x2 + cos x d. f(x) = 2x - x2
13
Soal:
Periksa apakah fungsi berikut adalah fungsi genap atau fungsi
ganjil atau bukan kedua-duanya.
a. f(x) = 1 - x4 b. f(x) = x + sin x
c. f(x) = x2 + cos x d. f(x) = 2x - x2
14. Fungsi naik dan fungsi turun
Definisi: 1. Fungsi f disebut naik pada selang I jika
f(x1) < f(x2) untuk setiap x1 < x2 di I.
2. Fungsi f disebut turun pada selang I jika
f(x1) > f(x2) untuk setiap x1 < x2 di I.
x1
y
f(x1)
x
y = f(x)
x2
f(x2)
Fungsi f naik
x1
y
f(x2)
x
y = f(x)
x2
f(x1)
Fungsi f turun

14. Soal:
Periksa apakah fungsi f berikut adalah fungsi naik atau fungsi
turun pada selang I.
a. f(x) = x2 I = [0, )
b. f(x) = sin x I = [ , 2]
15. Fungsi Baru dari Fungsi Lama
Dari fungsi dasar dapat dibentuk fungsi baru dengan cara:
1. Transformasi fungsi: pergeseran, peregangan dan pencerminan
2. Operasi aljabar fungsi: penambahan, pengurangan, perkalian
dan pembagian
3. Komposisi fungsi
Transformasi fungsi
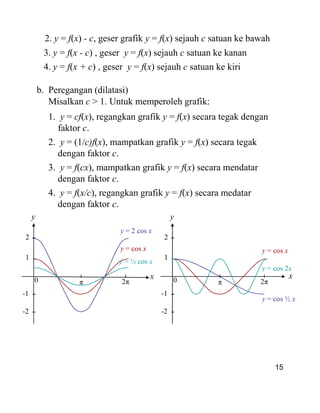
a. Pergeseran (translasi)
Misalkan c > 0, diperoleh 4 macam grafik:
1. y = f(x) + c, geser y = f(x) sejauh c satuan ke atas
14
15. Fungsi Baru dari Fungsi Lama
Dari fungsi dasar dapat dibentuk fungsi baru dengan cara:
1. Transformasi fungsi: pergeseran, peregangan dan pencerminan
2. Operasi aljabar fungsi: penambahan, pengurangan, perkalian
dan pembagian
3. Komposisi fungsi
Transformasi fungsi
a. Pergeseran (translasi)
Misalkan c > 0, diperoleh 4 macam grafik:
1. y = f(x) + c, geser y = f(x) sejauh c satuan ke atas
y = f(x)
c
y
x
c
c
c
y = f(x-c)y = f(x+c)
y = f(x) - c
y = f(x) + c

15. b. Peregangan (dilatasi)
Misalkan c > 1. Untuk memperoleh grafik:
1. y = cf(x), regangkan grafik y = f(x) secara tegak dengan
faktor c.
2. y = (1/c)f(x), mampatkan grafik y = f(x) secara tegak
dengan faktor c.
3. y = f(cx), mampatkan grafik y = f(x) secara mendatar
dengan faktor c.
4. y = f(x/c), regangkan grafik y = f(x) secara medatar
dengan faktor c.
2. y = f(x) - c, geser grafik y = f(x) sejauh c satuan ke bawah
3. y = f(x - c) , geser y = f(x) sejauh c satuan ke kanan
4. y = f(x + c) , geser y = f(x) sejauh c satuan ke kiri
15
b. Peregangan (dilatasi)
Misalkan c > 1. Untuk memperoleh grafik:
1. y = cf(x), regangkan grafik y = f(x) secara tegak dengan
faktor c.
2. y = (1/c)f(x), mampatkan grafik y = f(x) secara tegak
dengan faktor c.
3. y = f(cx), mampatkan grafik y = f(x) secara mendatar
dengan faktor c.
4. y = f(x/c), regangkan grafik y = f(x) secara medatar
dengan faktor c.
0 π 2π
-1
1
y
y = cos x
2
-2
y = 2 cos x
y = ½ cos x
x 0 π 2π
-1
1
y
y = cos x
2
-2
x
y = cos ½ x
y = cos 2x

16. c. Pencerminan
Untuk memperoleh grafik:
1. y = -f(x), cerminkan grafik y = f(x) terhadap sumbu-x
2. y = f(-x), cerminkan grafik y = f(x) terhadap sumbu-y
y
x
y = f(x)
y = -f(x)
x
y = f(x)y = f(-x)
y
x-xx
f(x)
f(x)
-f(x)
Contoh:
Gambarkan grafik fungsi berikut dengan menggunakan
sifat transformasi fungsi.
1. f(x)= |x-1| 2. f(x) = x2+2x+1
3. f(x)= sin 2x 4. f(x) = 1 - cos x
16
Contoh:
Gambarkan grafik fungsi berikut dengan menggunakan
sifat transformasi fungsi.
1. f(x)= |x-1| 2. f(x) = x2+2x+1
3. f(x)= sin 2x 4. f(x) = 1 - cos x

17. OPERASI FUNGSI ALJABAR
Definisi: [Aljabar fungsi]
Misalkan f dan g adalah fungsi dengan daerah asal Df dan
Dg. Fungsi f+g, f-g, fg dan f/g didefinisikan sebagai berikut
1. (f + g)(x) = f(x) + g(x) Df+g = Df Dg.
2. (f - g)(x) = f(x) - g(x) Df-g = Df Dg.
3. (fg)(x) = f(x) g(x) Dfg = Df Dg.
4. (f/g)(x) = f(x)/g(x) Df/g = {Df Dg.} – {x | g(x)= 0}
Contoh:
Tentukan f+g, f-g, fg dan f/g beserta daerah asalnya, jika
17
2
( ) ( )
( ) 1
1.
2 ). ( 1
f x x g x x
f x x g x x
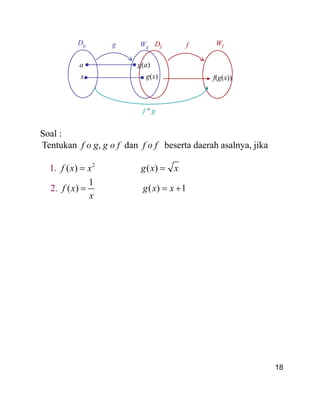
Komposisi fungsi
Definisi: [Komposisi fungsi]
Misalkan f dan g adalah fungsi dengan daerah asal Df dan
Dg. Fungsi komposisi f o g didefinisikan sebagai berikut:
(f o g)(x) = f(g(x))
di mana Df o g = {x є Dg | g(x) є Df }

18. Soal :
Tentukan f o g, g o f dan f o f beserta daerah asalnya, jika
2
1.
2.
( ) ( )
1
( ) ( ) 1
f x x g x x
f x g x x
x
Dfg f WfWg
Dg
x
g(a)
f(g(x))
a
g(x)
f ° g
18