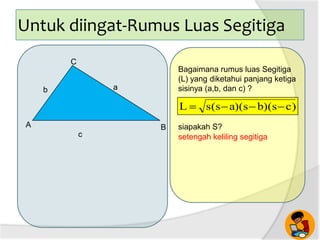
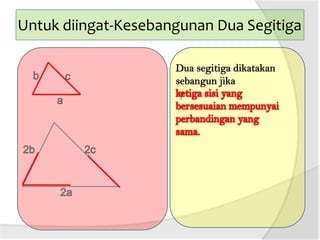
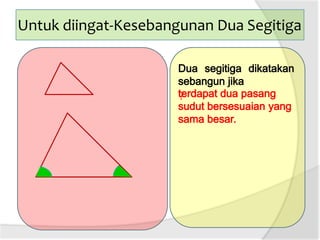
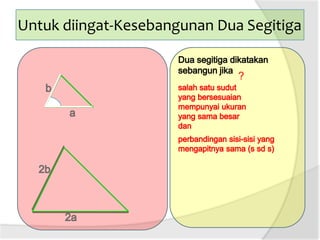
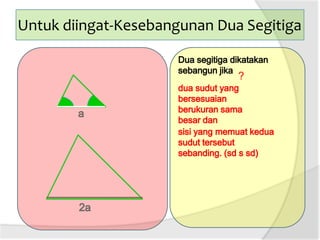
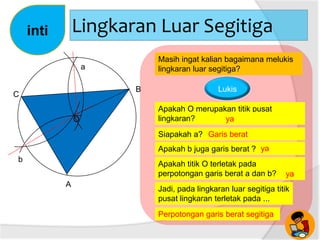
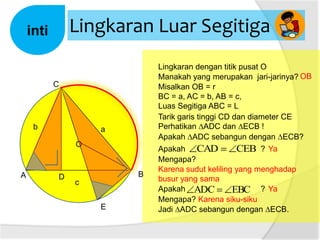
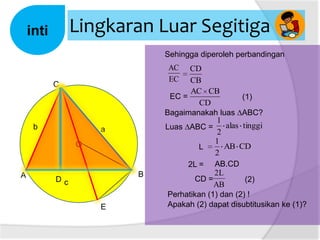
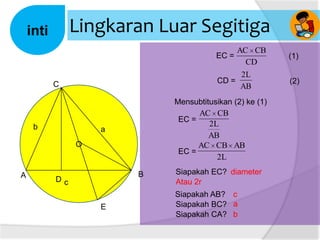
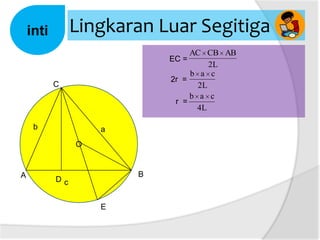
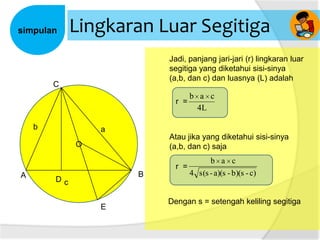
Dokumen ini membahas tentang panjang jari-jari lingkaran luar segitiga, termasuk cara menggambar lingkaran luar dan hubungan antara sudut pusat dengan sudut keliling. Terdapat penjelasan tentang rumus luas segitiga dan kelilingnya. Selain itu, dijelaskan juga bagaimana menentukan jari-jari lingkaran luar segitiga dengan menggunakan panjang sisi dan luas segitiga.

1. © 2013

2. Kampus UNNES tanpa asap klapot
(1 Januari 2013)

4. Materi Pokok :
Panjang Jari-jari Lingkaran dalam Segitiga dan luar Segitga
Standar Kompetensi :
Menentukan unsur, bagian lingkaran serta ukurannya.
Kompetensi Dasar :
Melukis lingkaran dalam dan lingkaran luar suatu segitiga.
Indikator :
1. Menemukan rumus panjang jari-jari lingkaran luar segitiga.
2. Menyelesaikan soal yang berkaitan dengan jari-jari lingkaran luar segitiga.
Muhamad Husni Mubaraq
Pendidikan Matematika
4101410001
@IDbaraq

5. PETUNJUK
Adapun caranya adalah:
CD Pembelajaran ini
memuat serangkaian
per-tanyaan kognitif
(good questions).
Peserta didik dapat
mencapai tujuan
pembelajaran dengan
mudah dengan cara
menjawab semua
pertanyaan tersebut.
CD pembelajaran ini
efektif apabila
digunakan secara
tepat
1. Klik, untuk memunculkan
informasi / pertanyaan
2. Klik berikutnya setelah
peserta didik menjawab
pertanyaan dengan benar
(beri keempatan
berpikir, jangan klik sebelum
siswa menjawab)
3. Begitu seterusnya sampai
siswa menemukan sim-pulan

6. Untuk diingat- Sudut pusat dan sudut keliling
Apakah sudut BDA sudut keliling
lingkaran? ya
Apakah sudut BDA menghadap
busur AB? ya
Apakah sudut BCA sudut keliling
lingkaran? ya
Apakah sudut BCA menghadap
busur AB? ya
Bagaimanakah besar sudut BCA
dengan sudut BDA? sama
Adakah sudut keliling lain yang
besarnya sama denga sudut BCA?
tidak
C
D
E
O
B
A
Jadi, sudut-sudut keliling
yang menghadap busur
yang sama besarnya
sama

7. Untuk diingat- Sudut pusat dan sudut keliling
Apakah sudut BCE merupakan sudut
keliling? ya
Apakah BE diameter lingkaran? ya
Apakah sudut BCE menghadap
diameter lingkaran BE? ya
Siapakah sudut BCE?
Sudut keliling lingkaran yang
menghadap diameter lingkaran
C
D
E
O
B
A

8. Untuk diingat- Sudut pusat dan sudut keliling
Manakah yang merupakan sudut
pusat? Sudut BOA Sudut AOE
Apakah sudut BOA menghadap
busur AB? ya
Apakah sudut keliling BDA
menghadap busur AB? ya
Bagaimanakah besar sudut
BOA? 2 x besar sudut BDA
Jadi besar sudut pusat sama
dengan ...2 x besar sudut keliling
Jika ... menghadap busur yang sama
C
D
E
O
B
A

9. Untuk diingat-Rumus Luas Segitiga
C
A
D
B
Masih ingat rumus luas daerah Segitiga? YA
Bagaimanakah rumus luas daerah segitiga (L) dengan
tinggi (t) dan alas (a)?
1
L
a t
2

10. Untuk diingat-Keliling Segitiga
C
A
Misalkan k = 2s
Maka,
1
s = ... k
2
a
b
c
Masih ingat bagaimana cara menentukan
keliling Segitiga? YA
Bagaimanakah keliling Segitiga (k)
pada gambar di atas?
k a b c
1
a
2
B
s
b
c
1
a
2
b
c
Maka s merupakan ...
Setengah keliling segitiga

11. Untuk diingat-Rumus Luas Segitiga
C
Bagaimana rumus luas Segitiga
(L) yang diketahui panjang ketiga
sisinya (a,b, dan c) ?
a
b
L
A
c
B
s(s a)(s b)(s c)
siapakah S?
setengah keliling segitiga

12. Untuk diingat-Kesebangunan Dua Segitiga
?

13. Untuk diingat-Kesebangunan Dua Segitiga
?

14. Untuk diingat-Kesebangunan Dua Segitiga
?

15. Untuk diingat-Kesebangunan Dua Segitiga
?

16. Lingkaran Luar Segitiga
inti
Masih ingat kalian bagaimana melukis
lingkaran luar segitiga?
a
B
C
O
Lukis
Apakah O merupakan titik pusat
lingkaran?
ya
Siapakah a? Garis berat
Apakah b juga garis berat ? ya
b
Apakah titik O terletak pada
perpotongan garis berat a dan b?
A
ya
Jadi, pada lingkaran luar segitiga titik
pusat lingkaran terletak pada ...
Perpotongan garis berat segitiga

17. Lingkaran Luar Segitiga
inti
Lingkaran dengan titik pusat O
Manakah yang merupakan jari-jarinya? OB
Misalkan OB = r
BC = a, AC = b, AB = c,
Luas Segitiga ABC = L
Tarik garis tinggi CD dan diameter CE
Perhatikan ∆ADC dan ∆ECB !
Apakah ∆ADC sebangun dengan ∆ECB?
C
b
a
O
A
D
B
c
E
Apakah CAD
CEB ? Ya
Mengapa?
Karena sudut keliling yang menghadap
busur yang sama
Apakah ADC
EBC ? Ya
Mengapa? Karena siku-siku
Jadi ∆ADC sebangun dengan ∆ECB.

18. Lingkaran Luar Segitiga
inti
Sehingga diperoleh perbandingan
AC
EC
C
b
a
O
A
B
Dc
E
CD
CB
AC CB
EC =
(1)
CD
Bagaimanakah luas ∆ABC?
1
alas tinggi
Luas ∆ABC =
2
1
AB CD
L
2
2L = AB.CD
2L
CD =
(2)
AB
Perhatikan (1) dan (2) !
Apakah (2) dapat disubtitusikan ke (1)?

19. Lingkaran Luar Segitiga
inti
EC =
CD =
C
b
a
B
Dc
E
2L
AB
Mensubtitusikan (2) ke (1)
AC CB
EC =
2L
AB
AC CB AB
EC =
2L
O
A
AC CB
CD
Siapakah EC? diameter
Atau 2r
Siapakah AB? c
Siapakah BC? a
Siapakah CA? b
(1)
(2)

20. Lingkaran Luar Segitiga
inti
AC CB AB
2L
b a c
2r =
2L
b a c
r =
4L
EC =
C
b
a
O
A
B
Dc
E

21. simpulan
Lingkaran Luar Segitiga
Jadi, panjang jari-jari (r) lingkaran luar
segitiga yang diketahui sisi-sinya
(a,b, dan c) dan luasnya (L) adalah
C
r =
b
a
Atau jika yang diketahui sisi-sinya
(a,b, dan c) saja
O
A
b a c
4L
B
Dc
E
b a c
r =
4 s(s - a)(s - b)(s - c)
Dengan s = setengah keliling segitiga

22. Lagu
Ayo kawan ingat
Panjang jari-jari
Lagu :
Potong Bebek
Angsa
Lirik oleh :
Muhamad Husni M.
Lingkaran luar
Segitiga itu
Perkalian panjang
sisi-sisinya
dibagi empat luas segitiga
Mulai

23. Muhamad Husni Mubaraq
Pendidikan Matematika
4101410001
@IDbaraq
© 2013