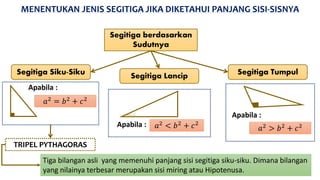
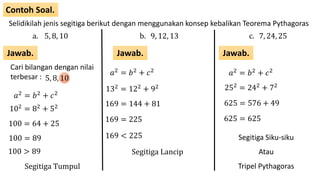
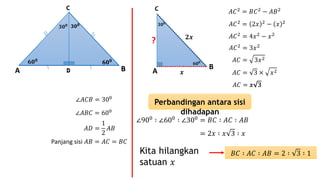
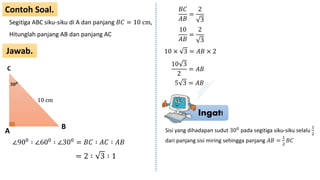
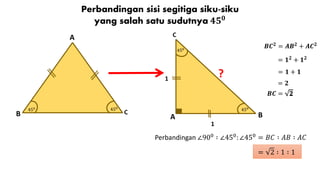
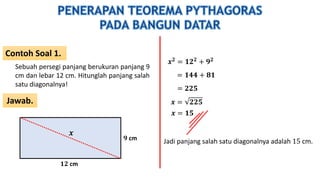
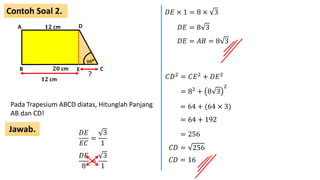
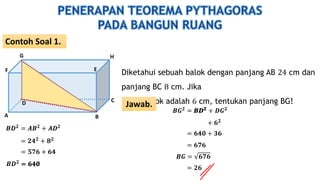
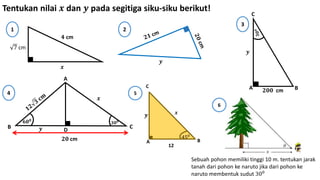
Dokumen ini membahas kebalikan teorema Pythagoras untuk menentukan jenis segitiga berdasarkan panjang sisi-sisinya dan sudutnya, serta memberikan contoh soal dan cara menghitung panjang sisi segitiga. Selain itu, terdapat penjelasan tentang perbandingan sisi pada segitiga siku-siku dan contoh perhitungan panjang diagonal pada bangun datar lainnya. Dokumen ini juga menyertakan beberapa soal latihan dengan jawaban lengkap.

2. KEBALIKAN TEOREMA PYTHAGORAS
x
y
C
A B
𝑎
𝑐
𝑏2 = 𝑎2 + 𝑐2 maka segitiga ABC siku-siku di B
𝑏
𝑎2 = 𝑏2 + 𝑐2 maka segitiga ABC siku-siku di A
𝑐2
= 𝑎2
+ 𝑏2
maka segitiga ABC siku-siku di C

3. MENENTUKAN JENIS SEGITIGA JIKA DIKETAHUI PANJANG SISI-SISNYA
Segitiga berdasarkan
Sudutnya
Segitiga Siku-Siku Segitiga Lancip Segitiga Tumpul
Apabila :
𝑎2 = 𝑏2 + 𝑐2
𝑎2 < 𝑏2 + 𝑐2Apabila : 𝑎2 > 𝑏2 + 𝑐2
Apabila :
TRIPEL PYTHAGORAS
Tiga bilangan asli yang memenuhi panjang sisi segitiga siku-siku. Dimana bilangan
yang nilainya terbesar merupakan sisi miring atau Hipotenusa.

4. Contoh Soal.
Jawab.
Selidikilah jenis segitiga berikut dengan menggunakan konsep kebalikan Teorema Pythagoras
a. 5, 8, 10 b. 9, 12, 13 c. 7, 24, 25
Jawab. Jawab.
Cari bilangan dengan nilai
terbesar : 5, 8, 10
𝑎2
= 𝑏2
+ 𝑐2
102 = 82 + 52
100 = 64 + 25
100 = 89
100 > 89
Segitiga Tumpul
𝑎2 = 𝑏2 + 𝑐2
132 = 122 + 92
169 = 144 + 81
169 = 225
169 < 225
Segitiga Lancip
𝑎2 = 𝑏2 + 𝑐2
252 = 242 + 72
625 = 576 + 49
625 = 625
Segitiga Siku-siku
Atau
Tripel Pythagoras

5. x
y Contoh Soal.
Jawab.
Tentukan jarak antara dua titik dari pasangan titik
(10, 20) dan (15, 25)
10 2015 25
10
20
15
25
A
B
𝐴𝐵 = 15 − 10 2 + (25 − 20)
𝐴𝐵 = 52 + 52
𝐴𝐵 = 25 + 25
𝐴𝐵 = 50
𝐴𝐵 = 25 × 2
𝐴𝐵 = 5 2

6. 10/25/2017 Binti Wulandari Lailatul Rohmah 6

7.  Perbadingan segitiga siku-siku pada segitiga sama sisi yang salah satu sudutnya 𝟑𝟎 𝟎
𝒂𝒕𝒂𝒖 𝟔𝟎 𝟎
C
A BD
C
BD
𝟔𝟎 𝟎
𝟔𝟎 𝟎
𝟑𝟎 𝟎
𝟑𝟎 𝟎
A

8. ∠𝐴𝐶𝐵 = 300
∠𝐴𝐵𝐶 = 600
𝐴𝐷 =
1
2
𝐴𝐵
Panjang sisi 𝐴𝐵 = 𝐴𝐶 = 𝐵𝐶
A
C
B
𝟔𝟎 𝟎
𝟑𝟎 𝟎
𝒙
𝟐𝒙
?
𝐴𝐶2 = 𝐵𝐶2 − 𝐴𝐵2
𝐴𝐶2 = 2𝑥 2 − 𝑥 2
𝐴𝐶2 = 4𝑥2 − 𝑥2
𝐴𝐶2
= 3𝑥2
𝐴𝐶 = 3𝑥2
𝐴𝐶 = 3 × 𝑥2
𝐴𝐶 = 𝑥 3𝑥 3
Perbandingan antara sisi
dihadapan
∠900
∶ ∠600
∶ ∠300
= 𝐵𝐶 ∶ 𝐴𝐶 ∶ 𝐴𝐵
= 2𝑥 ∶ 𝑥 3 ∶ 𝑥
Kita hilangkan
satuan 𝑥
𝐵𝐶 ∶ 𝐴𝐶 ∶ 𝐴𝐵 = 2 ∶ 3 ∶ 1
A BD
C
𝟔𝟎 𝟎
𝟔𝟎 𝟎
𝟑𝟎 𝟎 𝟑𝟎 𝟎
BD
C
𝟔𝟎 𝟎
𝟑𝟎 𝟎
D
𝟑𝟎 𝟎
𝟔𝟎 𝟎

9. Ingat!
Contoh Soal.
Jawab.
Segitiga ABC siku-siku di A dan panjang 𝐵𝐶 = 10 cm,
Hitunglah panjang AB dan panjang AC
A
C
B
𝟑𝟎 𝟎
∠900
∶ ∠600
∶ ∠300
= 𝐵𝐶 ∶ 𝐴𝐶 ∶ 𝐴𝐵
= 2 ∶ 3 ∶ 1
10 cm
𝐵𝐶
𝐴𝐵
=
2
3
10
𝐴𝐵
=
2
3
10 × 3 = 𝐴𝐵 × 2
10 3
2
= 𝐴𝐵
5 3 = 𝐴𝐵
Sisi yang dihadapan sudut 300 pada segitiga siku-siku selalu
1
2
dari panjang sisi miring sehingga panjang 𝐴𝐵 =
1
2
𝐵𝐶

10. Perbandingan sisi segitiga siku-siku
yang salah satu sudutnya 𝟒𝟓 𝟎
A
C
B
A
B C450 450
450
450
1
1
?
𝑩𝑪 𝟐 = 𝑨𝑩 𝟐 + 𝑨𝑪 𝟐
= 𝟏 𝟐 + 𝟏 𝟐
= 𝟏 + 𝟏
= 𝟐
𝑩𝑪 = 𝟐𝟐
Perbandingan ∠900
∶ ∠450
: ∠450
= 𝐵𝐶 ∶ 𝐴𝐵 ∶ 𝐴𝐶
= 2 ∶ 1 ∶ 1

11. 10/25/2017 Binti Wulandari Lailatul Rohmah 11

12. Contoh Soal 1.
Jawab.
Sebuah persegi panjang berukuran panjang 9
cm dan lebar 12 cm. Hitunglah panjang salah
satu diagonalnya!
𝟏𝟐 cm
𝟗 cm
𝒙
𝒙 𝟐 = 𝟏𝟐 𝟐 + 𝟗 𝟐
= 𝟏𝟒𝟒 + 𝟖𝟏
= 𝟐𝟐𝟓
𝒙 = 𝟐𝟐𝟓
𝒙 = 𝟏𝟓
Jadi panjang salah satu diagonalnya adalah 15 cm.

13. Contoh Soal 2.
Jawab.
A
B C
D
𝟐𝟎 cm
𝟏𝟐 cm
𝟔𝟎 𝟎
Pada Trapesium ABCD diatas, Hitunglah Panjang
AB dan CD!
E
𝐷𝐸
𝐸𝐶
=
3
1
𝟏𝟐 cm
?
𝐷𝐸
8
=
3
1
𝐷𝐸 × 1 = 8 × 3
𝐷𝐸 = 8 3
𝐷𝐸 = 𝐴𝐵 = 8 3
𝐶𝐷2 = 𝐶𝐸2 + 𝐷𝐸2
= 82 + 8 3
2
= 64 + (64 × 3)
= 64 + 192
= 256
𝐶𝐷 = 256
𝐶𝐷 = 16

14. A B
CD
F E
HG
Diketahui sebuah balok dengan panjang AB 24 cm dan
panjang BC 8 cm. Jika
tinggi balok adalah 6 cm, tentukan panjang BG!Jawab.
Contoh Soal 1.
𝑩𝑫 𝟐 = 𝑨𝑩 𝟐 + 𝑨𝑫 𝟐
= 𝟐𝟒 𝟐
+ 𝟖 𝟐
= 𝟓𝟕𝟔 + 𝟔𝟒
𝑩𝑫 𝟐 = 𝟔𝟒𝟎
𝑩𝑮 𝟐 = 𝑩𝑫 𝟐 + 𝑫𝑮 𝟐𝑩𝑫 𝟐
= 𝟔𝟒𝟎
+ 𝟔 𝟐
= 𝟔𝟒𝟎 + 𝟑𝟔
= 𝟔𝟕𝟔
𝑩𝑮 = 𝟔𝟕𝟔
= 𝟐𝟔

16. 𝟒 cm
7 cm
𝒙
1 2
𝒚
Tentukan nilai 𝒙 dan 𝒚 pada segitiga siku-siku berikut!
𝟐𝟎𝟎 cmA B
C
𝒚
3
4
A
B C
D
𝟑𝟎 𝟎𝟔𝟎 𝟎
𝟐𝟎 cm
𝒙
𝒚
A B
450
12
𝒙
C
5
𝒚
Sebuah pohon memiliki tinggi 10 m. tentukan jarak
tanah dari pohon ke naruto jika dari pohon ke
naruto membentuk sudut 300
6