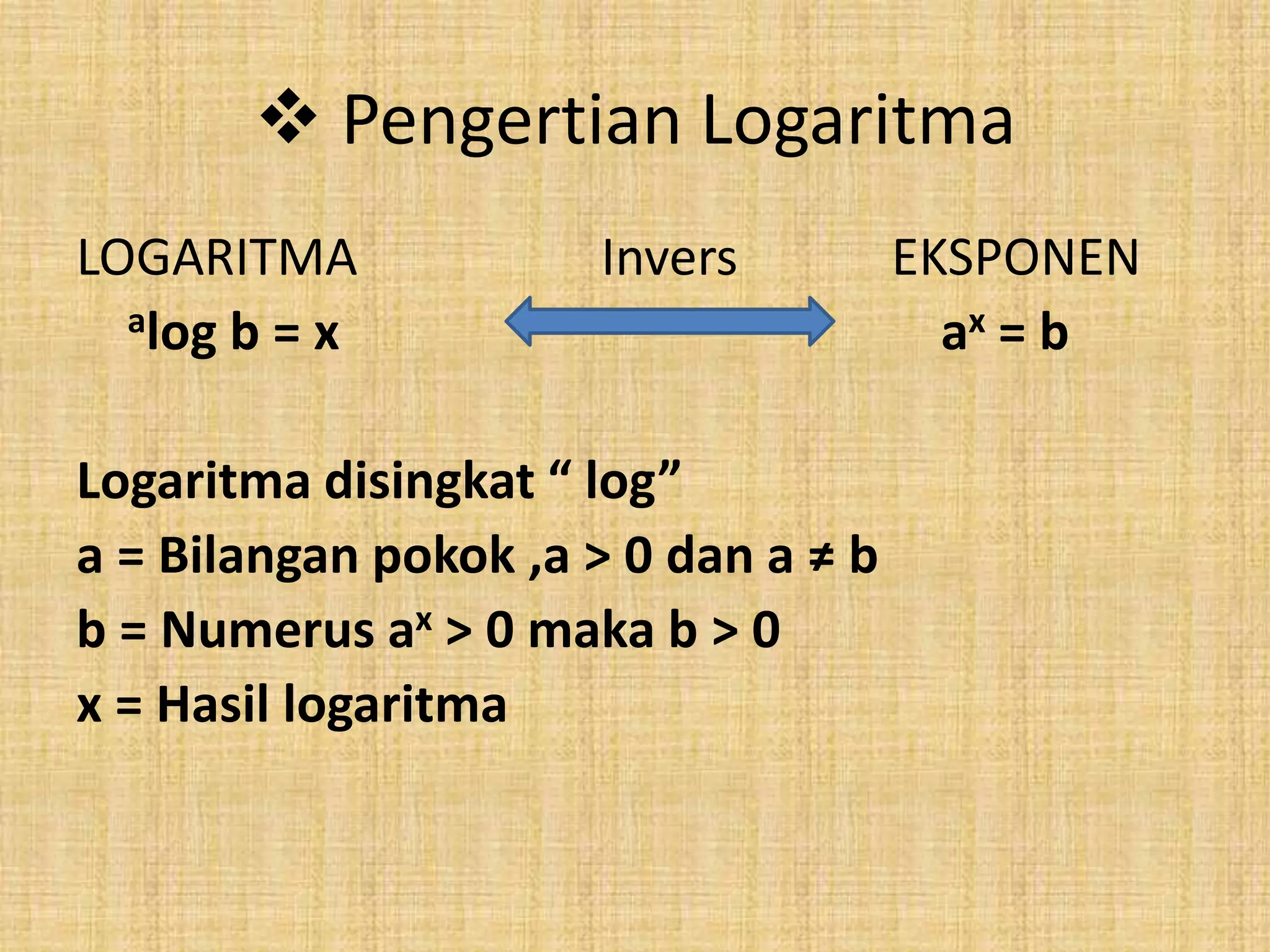
Dokumen ini membahas logaritma sebagai alat untuk memecahkan masalah terkait bentuk pangkat, akar, dan logaritma, dengan tujuan pembelajaran yang mencakup konversi antara bentuk pangkat dan logaritma serta operasi aljabar. Logaritma digunakan dalam berbagai bidang seperti pengukuran skala gempa, astronomi, dan biologi. Terdapat juga contoh-contoh soal dan cara menghitung logaritma menggunakan kalkulator.

1. LOGARITMA
SK: 1. Memecahkan masalah yang berkaitan
dengan bentuk pangkat ,akar dan logaritma.
Tujuan Pembelajaran :
1. Peserta didik dapat mengubah bentuk pangkat ke bentuk
logaritma, dan sebaliknya.
2. Peserta didik dapat melakukan operasi aljabar pada Bentuk
logaritma.

2. Manfaat mempelajari logaritma
• Penggunaan logaritma yang paling jelas adalah pada
penghitungan skala Richter untuk gempa bumi dan
desibel.
• Para astronom masih menggunakan skala logaritmik
untuk sumbu grafik dan diagram.
• Logaritma juga diaplikasikan dalam penghitungan
frekuensi musik.
• Penggunaan lain fungsi logaritma adalah dalam bidang
biologi, yaitu untuk mengukur laju pertumbuhan
penduduk, antropologi, dan keuangan (untuk
menghitung bunga majemuk).

3. Sub pokok bahasan:
Pengertian Logaritma
 Sifat – sifat Logaritma

4. Ingat ,,,,,,,,,,!!!
Eksponen (Pangkat)
ax = b
Ket :
a = basis (bilangan pokok)
x = pangkat
b = hasil eksponen

5.  Pengertian Logaritma
LOGARITMA Invers EKSPONEN
alog b = x ax = b
Logaritma disingkat “ log”
a = Bilangan pokok ,a > 0 dan a ≠ b
b = Numerus ax > 0 maka b > 0
x = Hasil logaritma

6. Contoh :
1. Ubahlah ke dalam bentuk logaritma
• 23 = 8
Penyelesaian : 23 = 8 → 2log 8 = 3
•
Penyelesaian : →
2. Tentukan nilai x dari

7. Penyelesaian :

8. 3.Jika dan 2log y = 3 tentukan nilai dari
a. x . y
b.
Jawab:

9. Latihan
Halaman 20 Buku “MATEMATIKA “
Kelas X terbitan yudistira
No 1.a,b,c,d,e,f
No 2.a,b,c,d,e,f
No 3.a,b,c,d,e,f
No 4.i dan ii
PR 4 iii dan iv

10. Sifat-Sifat Logaritma

11. Contoh Soal
1. Jika log 100 = x
Tentukan nilai x = ….
Jawab:
log 100 = x  10x = 100
10x = 102
x = 2.

12. Contoh Soal
2. Nilai dari 2log 8 + 3log 9 = ….
Jawab:
= 2log 8 + 3log 9
= 2log 23 + 3log 32
= 3 + 2
= 5

13. Contoh Soal
3. Nilai dari 2log (8 x 16) = ….
Jawab:
= 2log 8 + 2log 16
= 2log 23 + 2log 24
= 3 + 4
= 7

14. Contoh Soal
4. Nilai dari 3log (81 : 27) = ….
Jawab:
= 3log 81 - 3log 27
= 3log 34 - 3log 33
= 4 - 3
= 1

15. Contoh Soal
5. Nilai dari 2log 84 = ….
Jawab:
= 2log 84
= 4 x 2log 23
= 4 x 3
= 12

16. Contoh Soal
6. Nilai dari 2log 84 = ….
Jawab:
= 2log 84 
= 2 x 2log 23
= 2 x 3
= 6
2
4 2log 8=

17. Contoh
7. Dari sifat logaritma yang ke-5 dan ke-6
berikut:

18. Contoh
8. Sifat ke 5,ke 10 dalam buku yudistira sifat
logarima ke 6

19. Contoh
9. Diketahui
log 40 = A dan log 2 = B, tentukan nilai dari log 20
Pembahasan
log 20 = log 40/2 = log 40 − log 2 = A − B
10. Diketahui:
log p = A
log q = B
Tentukan nilai dari log p3 q2
Pembahasan
log p3 q2 = log p3 + log q2 = 3 log p + 2 log q = 3A + 2B

20. Menentukan nilai logaritma
menggunakan kalkulator
Misalkan menentukan logaritma tentukan log2
Jenis I : tekan log→2→=
Jenis II : tekan 2 → log
Latihan :
1. Log 2,124=
2. Log 1478=
3. Log 0,0005214=

21. Menentukan nilai logaritma suatu
bilangan lebih dari

22. Contoh :
1. Log 234.000 = log(2,34 X 10⁵)
= log 2,34 + log 10⁵
= 0,369+5
= 5,369
2.

23. Menentukan antilogaritma
Dalam Antilogaritma hasil logaritma
yang
diketahui dan numerus tidak diketahui.
Dengan menggunakan tabel logaritma
dan kalkulator

24. Dengan menggunakan tabel

26. Contoh
Log x = 1,410
Log x =0,410 +1
x= antilog 0,410 X antilog 1
x=2,62X10^1
=26,8

27. Menggunakan kalkulator
Contoh : log x =2,3
Jenis I tekan tombol 2ndF log 2 . 3 =
Jenis I tekan tombol 2nd log 2 . 3 =
Jenis I tekan tombol Shift log 2 . 5 =
Jenis I tekan tombol Inv Log 2 . 5 =
Jenis I tekan tombol 2 . 5 Inv Log