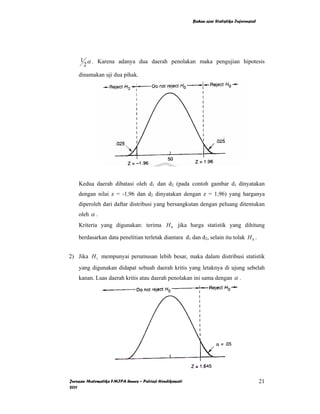
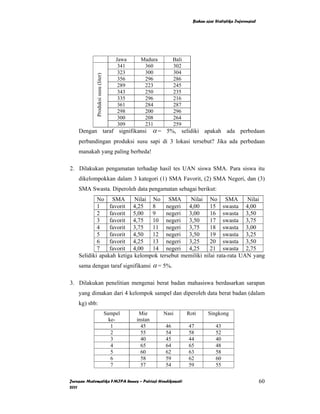
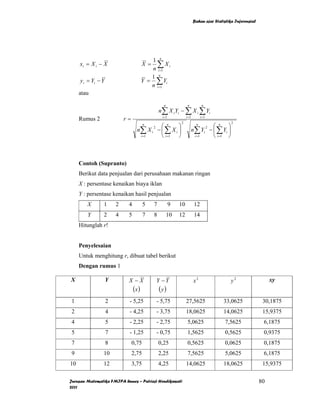
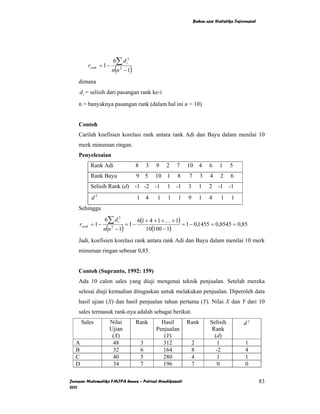
Dokumen ini adalah bahan ajar statistika inferensial yang mencakup penaksiran parameter, pengujian hipotesis, analisis varians, regresi, dan korelasi. Ditulis oleh Putriaji Hendikawati dari Jurusan Matematika FMIPA Universitas Negeri Semarang, dokumen ini memberikan pemahaman tentang metode penaksiran, termasuk cara menaksir rata-rata, proporsi, dan simpangan baku dengan menggunakan interval kepercayaan. Materi ini bersifat edukatif dan ditujukan untuk membantu siswa memahami konsep-konsep dasar dalam statistika inferensial.