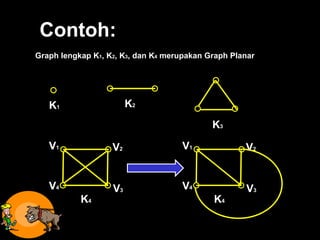
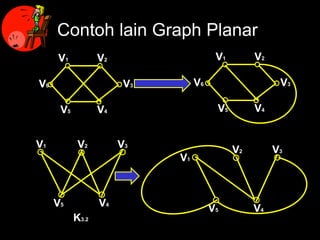
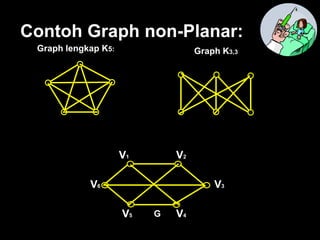
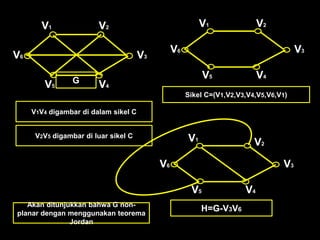
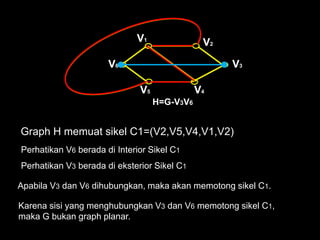
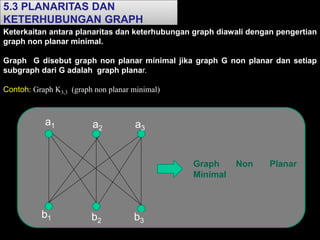
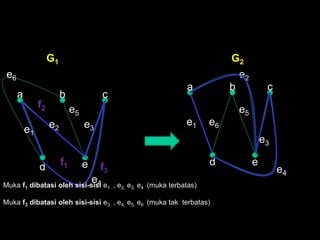
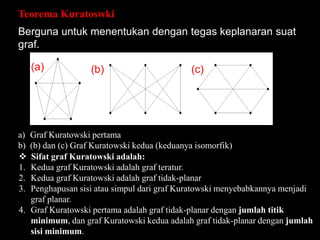
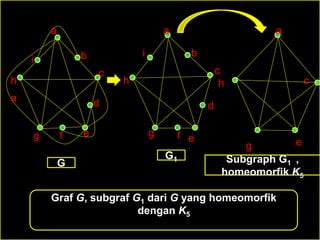
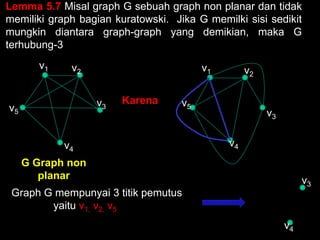
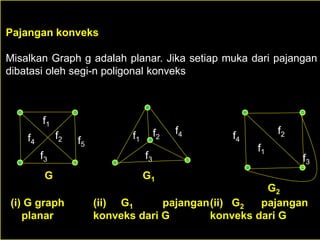
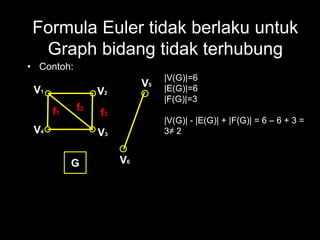
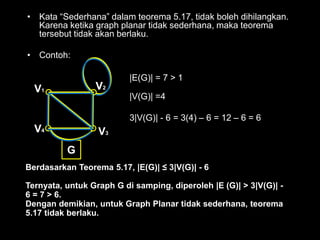
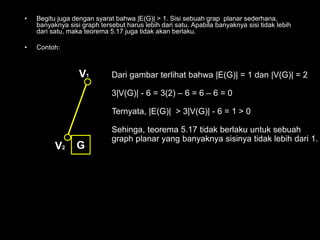
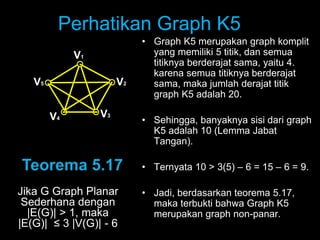
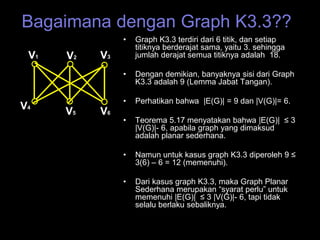
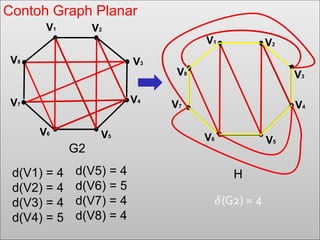
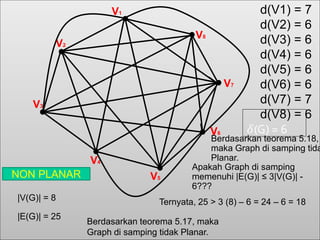
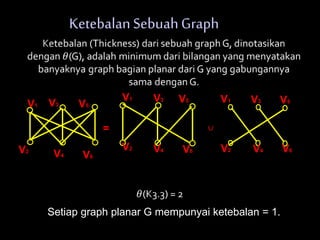
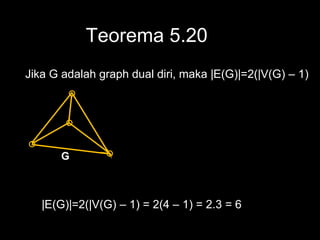
Dokumen ini membahas tentang graf planar, yang dapat digambarkan di bidang datar tanpa sisi yang saling berpotongan, serta perbedaan antara graf planar dan graf non-planar. Ada penjelasan terkait teorema-teorema kurva Jordan dan Kuratowski untuk mengidentifikasi sifat planaritas sebuah graf. Selain itu, terdapat pula contoh serta teori Euler terkait jumlah titik, sisi, dan muka dalam graf planar.

1. Matematika Diskrit
GRAPH PLANAR DAN GRAPH
BIDANG

2. GRAPH PLANAR & GRAPH BIDANG
• Graph G disebut Graph Planar jika G dapat digambar
pada bidang datar sedimikian sehingga sisi-sisinya
tidak ada yang saling berpotongan kecuali mungkin
pada titik-titik dari sisi-sisi tersebut.
Graph Bidangpasti Graph Planar,tetapi sebaliknya tidak
berlaku
• Graph bidang atau pajangan G adalah graph planar
G yang digambar pada bidang datar sedemikian
sehingga tidak ada sisi-sisinya yang saling berpotongan
kecuali mungkin pada titik-titik akhir sisi-sisi tersebut.

3. Contoh:
Graph lengkap K1, K2, K3, dan K4 merupakan Graph Planar
K1 K2
K3
K4
V1 V2
V3
V4
K4
V1 V2
V3
V4

4. Contoh lain Graph Planar
V1 V2
V3
V4V5
V6
V1 V2
V3
V4V5
V6
V1
V2 V3
V4V5
V1 V2 V3
V4V5
K3.2

5. Graph K3,3
Contoh Graph non-Planar:
Graph lengkap K5:
V1 V2
V3
V4V5
V6
G

6. X
Y
JD
TEOREMA KURVA JORDAN:
Misalkan J adalah sebuah kurva tertutup sederhana pada
sebuah bidang datar D.
Titik X terletak di Interior J dan titik Y terletak di eksterior J.
Jika dibuat sebuah kurva yang menghubungkan titik X dan
titik Y pada bidang D, maka kurva tersebut pasti memotong
kurva J.
Teorema Kurva Jordan dapat
digunakan untuk menunjukkan
suatu graphbukan graph planar.

7. V1 V2
V3
V4V5
V6
V1
V2
V3
V4V5
V6
G
H=G-V3V6
V1 V2
V3
V4V5
V6
Sikel C=(V1,V2,V3,V4,V5,V6,V1)
V1V4 digambar di dalam sikel C
V2V5 digambar di luar sikel C
Akan ditunjukkan bahwa G non-
planar dengan menggunakan teorema
Jordan

8. Graph H memuat sikel C1=(V2,V5,V4,V1,V2)
V1
V2
V3
V4V5
V6
H=G-V3V6
Perhatikan V6 berada di Interior Sikel C1
Perhatikan V3 berada di eksterior Sikel C1
Apabila V3 dan V6 dihubungkan, maka akan memotong sikel C1.
Karena sisi yang menghubungkan V3 dan V6 memotong sikel C1,
maka G bukan graph planar.

9. Keterkaitan antara planaritas dan keterhubungan graph diawali dengan pengertian
graph non planar minimal.
Graph G disebut graph non planar minimal jika graph G non planar dan setiap
subgraph dari G adalah graph planar.
Contoh: Graph K3,3 (graph non planar minimal)
5.3 PLANARITAS DAN
KETERHUBUNGAN GRAPH
a1 a2 a3
b1 b2 b3
Graph Non Planar
Minimal

10. Subgraph
K3,3
a1 a2 a3
b1 b2
b3
a1 a2 a3
b1 b2 b3
a1 a2
a
3
b1 b2 b3
a1
a
3
a2
b1 b2 b3

11. Contoh: graph K5 (graph non planar minimal)
Graph Non Planar Minimal
a1
a2
a3
a4
a5

12. Subgraph
K5
a1
a2
a3
a4
a5
a1
a3
a4
a5
a1
a3
a5

13. a b c
d e
e1
e2 e3
e4
e5
e6
a b c
d e
e1
e2
e3
e4
e5
e6
G1 G2
f1
f2
f3
Muka f1 dibatasi oleh sisi-sisi e1 , e2, e3, e4 (muka terbatas)
Muka f3 dibatasi oleh sisi-sisi e3 , e4, e5, e6 (muka tak terbatas)

14. Lemma 5.8 Misalkan G sebuah graph terhubung-3 dengan
ǀV(G)ǀ≥5. Maka G memuat sisi e sedemikian hingga graph
G.e adalah graph terhubung-3
v1 v2
v3
v4
v5
v6
e
G
v1
v2
V3=v
6)
v4v5
G.e
e = v3 ,
v6
Mempunyai 3 titik pemutus
v2, v4, v6
v1
v3
v5
Mempunyai 3 titik pemutus
v2, e, v4
v1
v5

15. Teorema Kuratoswki
Berguna untuk menentukan dengan tegas keplanaran suat
graf.
(a) (b) (c)
a) Graf Kuratowski pertama
b) (b) dan (c) Graf Kuratowski kedua (keduanya isomorfik)
 Sifat graf Kuratowski adalah:
1. Kedua graf Kuratowski adalah graf teratur.
2. Kedua graf Kuratowski adalah graf tidak-planar
3. Penghapusan sisi atau simpul dari graf Kuratowski menyebabkannya menjadi
graf planar.
4. Graf Kuratowski pertama adalah graf tidak-planar dengan jumlah titik
minimum, dan graf Kuratowski kedua adalah graf tidak-planar dengan jumlah
sisi minimum.

16. TEOREMA KURATOWSKI
Graf G bersifat planar jika dan hanya jika ia tidak mengandung
subgraph yang sama dengan salah satu graf Kuratowski atau
homeomorfik (homeomorphic) dengan salah satu dari
keduanya
Contoh
a b
c
d e f
a
b
c
d e f
a c
d f
Graf G tidak planar karena ia mengandung subgraf yang
sama dengan K3,3

17. a
b
d
c
efg
h
a
a
b
c
d
fg
h
i
a
c
e eg
h
Graf G, subgraf G1 dari G yang homeomorfik
dengan K5
G
G1 Subgraph G1 ,
homeomorfik K5
i

18. Lemma 5.7 Misal graph G sebuah graph non planar dan tidak
memiliki graph bagian kuratowski. Jika G memilki sisi sedikit
mungkin diantara graph-graph yang demikian, maka G
terhubung-3
v1 v2
v3
v4
v5
v2
v1
v3
v4
v5
Karena
G Graph non
planar
v4
v3
Graph G mempunyai 3 titik pemutus
yaitu v1, v2, v5

19. Teorema 5.9 Misal G sebuah graph dan e ϵ E(G). Jika G.e
memiliki graph bagian kuratowski maka G juga memiliki graph
bagian kuratowski
v1 v1
v3
v2
e
v6
v7
v8
v9
v10
v1
v3
v6v7
v8
G
G.e
v2
v3
v4
v5
v6
v7
v8
v9 v10
Homeomorfik Graph
Kuratowski
e = v4, v5

20. Pajangan konveks
Misalkan Graph g adalah planar. Jika setiap muka dari pajangan
dibatasi oleh segi-n poligonal konveks
G G1
G2
(i) G graph
planar
(ii) G1 pajangan
konveks dari G
(ii) G2 pajangan
konveks dari G
f3
f2
f1
f4 f5
f1
f2
f3
f4
f1
f2
f3
f4

21. Formula Euler
Teorema 5.16:
Jika G Graph bidang terhubung, maka |V(G)|-|E(G)|+|F(G)|=2
• Contoh:
f2
f1
f3
f4
Graph G terdiri dari 4 muka (face)
G
F(G) = {f1, f2, f3, f4} →
|F(G)|=4
Graph G terdiri dari 6 titik (vertex)
V(G) = {V1, V2, V3, V4, V5, V6} →
|V(G)|=6
Graph G terdiri dari 8 sisi (edge)
E(G) = {V1V2,V2 V3, V3V4, V4V5,
V5V6, V6V1, V1V4, V2V5} →
|E(G)|=8
|V(G)|-|E(G)|+|F(G)|=2
6 – 8 + 4 = 2
V1 V2
V3
V4
V5
V6

22. Formula Euler tidak berlaku untuk
Graph bidang tidak terhubung
• Contoh:
V5
V6
G
f1
f2
f3
|V(G)|=6
|E(G)|=6
|F(G)|=3
|V(G)| - |E(G)| + |F(G)| = 6 – 6 + 3 =
3≠ 2
V1 V2
V3
V4

23. Teorema 5.17
Jika G Graph Planar Sederhana dengan
|E(G)| > 1, maka |E(G)| ≤ 3 |V(G)| - 6
Contoh akan ditinjau dari:
Graph G Terhubung
Graph G Tidak Terhubung

24. Graph Planar G terhubung
V1 V2
V3
V4V5
V6
|E(G)| = 8 > 1
|V(G)| = 6
3|V(G)| - 6 = 3(6) – 6 = 18 – 6=12
Jelas, 8 ≤ 12

25. • Kata “Sederhana” dalam teorema 5.17, tidak boleh dihilangkan.
Karena ketika graph planar tidak sederhana, maka teorema
tersebut tidak akan berlaku.
• Contoh:
V1
V2
V3
V4
G
|E(G)| = 7 > 1
|V(G)| =4
3|V(G)| - 6 = 3(4) – 6 = 12 – 6 = 6
Berdasarkan Teorema 5.17, |E(G)| ≤ 3|V(G)| - 6
Ternyata, untuk Graph G di samping, diperoleh |E (G)| > 3|V(G)| -
6 = 7 > 6.
Dengan demikian, untuk Graph Planar tidak sederhana, teorema
5.17 tidak berlaku.

26. • Begitu juga dengan syarat bahwa |E(G)| > 1. Sisi sebuah grap planar sederhana,
banyaknya sisi graph tersebut harus lebih dari satu. Apabila banyaknya sisi tidak lebih
dari satu, maka teorema 5.17 juga tidak akan berlaku.
• Contoh:
V1
V2 G
Dari gambar terlihat bahwa |E(G)| = 1 dan |V(G)| = 2
3|V(G)| - 6 = 3(2) – 6 = 6 – 6 = 0
Ternyata, |E(G)| > 3|V(G)| - 6 = 1 > 0
Sehinga, teorema 5.17 tidak berlaku untuk sebuah
graph planar yang banyaknya sisinya tidak lebih dari 1.

27. Perhatikan Graph K5
• Graph K5 merupakan graph komplit
yang memiliki 5 titik, dan semua
titiknya berderajat sama, yaitu 4.
karena semua titiknya berderajat
sama, maka jumlah derajat titik
graph K5 adalah 20.
• Sehingga, banyaknya sisi dari graph
K5 adalah 10 (Lemma Jabat
Tangan).
• Ternyata 10 > 3(5) – 6 = 15 – 6 = 9.
• Jadi, berdasarkan teorema 5.17,
maka terbukti bahwa Graph K5
merupakan graph non-panar.
V1
V2
V3
V4
V5
Jika G Graph Planar
Sederhana dengan
|E(G)| > 1, maka
|E(G)| ≤ 3 |V(G)| - 6

28. Bagaimana dengan Graph K3.3??
• Graph K3.3 terdiri dari 6 titik, dan setiap
titiknya berderajat sama, yaitu 3. sehingga
jumlah derajat semua titiknya adalah 18.
• Dengan demikian, banyaknya sisi dari Graph
K3.3 adalah 9 (Lemma Jabat Tangan).
• Perhatikan bahwa |E(G)| = 9 dan |V(G)|= 6.
• Teorema 5.17 menyatakan bahwa |E(G)| ≤ 3
|V(G)|- 6, apabila graph yang dimaksud
adalah planar sederhana.
• Namun untuk kasus graph K3.3 diperoleh 9 ≤
3(6) – 6 = 12 (memenuhi).
• Dari kasus graph K3.3, maka Graph Planar
Sederhana merupakan “syarat perlu” untuk
memenuhi |E(G)| ≤ 3 |V(G)|- 6, tapi tidak
selalu berlaku sebaliknya.
V2V1 V3
V4
V5 V6

29. Teorema 5.18
V1 V2
V3
V4V5
V6
G1
d(V1) = 3
d(V2) = 3
d(V3) = 2
d(V4) = 3
d(V5) = 3
d(V6) = 2

30. Contoh Graph Planar
V1 V2
V3
V4
V5
V6
V7
V8
G2
V1 V2
V3
V4
V5
V6
V7
V8
Hd(V1) = 4
d(V2) = 4
d(V3) = 4
d(V4) = 5
d(V5) = 4
d(V6) = 5
d(V7) = 4
d(V8) = 4
4

31. V1
V2
V3
V4
V5
V6
V7
V8
|V(G)| = 8
|E(G)| = 25
Apakah Graph di samping
memenuhi |E(G)| ≤ 3|V(G)| -
6???
Ternyata, 25 > 3 (8) – 6 = 24 – 6 = 18
Berdasarkan teorema 5.17, maka
Graph di samping tidak Planar.
d(V1) = 7
d(V2) = 6
d(V3) = 6
d(V4) = 6
d(V5) = 6
d(V6) = 6
d(V7) = 7
d(V8) = 6
Berdasarkan teorema 5.18,
maka Graph di samping tida
Planar.
NON PLANAR

32. KetebalanSebuahGraph
Setiap graph planar G mempunyai ketebalan = 1.
V1
V2
V3
V4 V6
V5
=
V5V1
V2
V3
V4 V6
V1
V2
V3
V4
V5
V6

33. Teorema 5.19
Dalam menentukan nilai eksak ketebalan sebuah
graph,tidak ada formula yang pasti yang dapat
digunakan. Tetapi dapat ditentukan berapa batas
bawah dari ketebalan suatu graph.

34. Graph Dual dari Graph Bidang
Graph H* merupakan graph dual dari H, karena:
1. Sebuah muka H berkorespondensi dengan sebuah titik di H*, atau
|F(H)|=|V(H*)|
2. Sebuah sisi H berkorespondensi dengan sisi di H*, atau |E(H)|=|E(H*)|
3. Sebuah muka berderajat k di H, berkorespondensi dengan sebuah titik
berderajat k di H*.
4. Sebuah titik berderajat 2 di H, berkorespondensi dengan sebuah sisi
rangkap di H*.
𝐇∗
f1
f2
f3
f4
f5
f6
V1
V2
V3
V4
V5
V6
H

35. • Graph H dan H* tidak isomorfik. Karena terdapat sebuah titik di H*
yang berderajat 5, sedangkan di H tidak terdapat titik yang
berderajat 5.
H
G
G*
Graph G dan G* isomorfik. Karena |V(G)|=|V(G*)|=4, |E(G)|=|E(G*)|=6,
dan derajat tiap titiknya sama.
Apabila graph planar isomorfik dengan dualnya, maka graph tersebut
disebut graph dual diri.

36. Teorema 5.20
Jika G adalah graph dual diri, maka |E(G)|=2(|V(G) – 1)
G
|E(G)|=2(|V(G) – 1) = 2(4 – 1) = 2.3 = 6

37. Graph Polyhedral
• Bangun ruang dimensi tiga yang dibatasi oleh permukaan-
permukaan yang berupa bidang datar polygonal (bidang
datar segi-n, n ≥ 3) disebut polyhedron.
• Titik-titik dan sisi-sisi dari sebuah polyhedron membentuk
sebuah graph sederhana di ruang dimensi 3. Jika titik-titik
dan sisi-sisinya terhubung dan membentuk graph bidang
(planar) sederhana, maka disebut graph polyhedral.

38. TERIMA KASIH
Presented by:
• KAHABUDDIN
• MUH. RUSLI JUNAID
• CITRA DEWI CHAIRANI