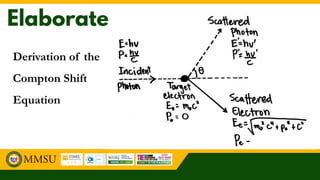
The document outlines key learning objectives regarding the Compton effect, including how x-rays are scattered by electrons, changes in wavelength, and comparisons with classical wave theory. It highlights practical applications such as x-ray imaging, x-ray diffraction, and security scanning. Additionally, it underscores the importance of the Compton effect in understanding light's wave-particle duality and its implications for fields like medicine and particle physics.

2. REPORTER:
ALEGADO, MARVIN C.

3. After the report, the students should be able to:
• explain how X-rays are scattered by electrons and how this leads to a
change in wavelength;
• compare classical wave theory with the observed results of the Compton
Effect;
• calculate the wavelength shift using the Compton formula; and
• explore practical applications of the Compton Effect, such as X-ray
imaging and diffraction.

6. We will further discuss the Compton effect, which
played a very important role in providing irrefutable
evidence for the picture of light, where light behaves
like packets or particles or photons.

7. 1. What do you think are
the similarities of the
billiard games to the
Compton effect?
2. How do they relate to
each other?

9. 1. What is the Compton Effect?
2. What changes do you observe in the scattered radiation compared to
the incident radiation?
3. What is the relationship between the scattering angle and the
wavelength shift?
4. How does the Compton Effect challenge classical wave theory?
5. What implications does the Compton Effect have for our understanding
of light?

11. A. Compton Effect Overview:
• When a high-energy photon (e.g., an X-ray) collides with an
electron, it transfers some of its energy and momentum to the
electron.
• As a result, the photon changes direction (scatters) and experiences
a wavelength shift (increase in wavelength).

12. B. Changes in Scattered Radiation:
• Compared to the incident radiation (original X-ray), the
scattered radiation has:
• Increased wavelength: The wavelength of the scattered
photon becomes longer.
• Decreased energy: The scattered photon loses energy during
the interaction.
• The Compton shift (Δλ) quantifies this change in
wavelength.

13. C. Scattering Angle and Wavelength Shift:
• The scattering angle (θ) between the incident and scattered
directions determines the amount of wavelength shift.
• The greater the scattering angle, the larger the wavelength shift.
o If ϑ is small, ∆λ is small.
o If ϑ is large, ∆λ is large.
• The relationship is described by Compton’s equation:
Δλ = h / (mec) * (1 - cos θ), where h is Planck’s constant, me is
the electron mass, and c is the speed of light.

14. D. Challenge to Classical Wave Theory:
• Classical wave theory predicts that the wavelength of scattered
radiation should remain unchanged.
• However, the Compton Effect demonstrates that light behaves as
both waves and particles (photons).
• This challenged classical physics and led to the development of
quantum mechanics.

15. CLASSICAL WAVE THEORY Observed Results of the Compton Effect
• When an electromagnetic wave (such as X-rays)
interacts with charged particles (such as
electrons), the scattered radiation should have the
same frequency and wavelength as the incident
radiation.
• In Thomson scattering, the electromagnetic field
of the incoming wave accelerates an electron via
the Lorentz force but does no work upon it.
• The electron oscillates at the same frequency as
the incoming wave and then re-emits (scatters)
light at that same frequency as a classical
oscillating electric dipole.
• This process is elastic, meaning no net energy is
given to the electron.
• The Compton Effect, observed experimentally,
contradicts classical predictions.
• When X-rays scatter off electrons, the scattered
light has a lower frequency and longer
wavelength than the incident X-rays.
• The frequency shift depends on the scattering
angle.
• Importantly, this behavior is not dependent on
the intensity (electric field amplitude) of the
incident radiation.
• The Compton Effect demonstrates that light
cannot be explained purely as a wave
phenomenon.
• Instead, it supports the photon model, where
light behaves as particles (photons) with
momentum and energy.

16. E. Implications for Our Understanding of Light:
• The Compton Effect solidifies the concept of wave-
particle duality.
• It shows that light cannot be purely explained as
continuous waves; it also exhibits particle-like
behavior.

17. Derivation of the
Compton Shift
Equation

18. Photons with a wavelength of 0.05 nm are scattered from a
sheet of carbon. What will be the wavelengths of the
photons that are scattered at:
a) 00
b) 450
c) 900
d) 1800

19. Practical
Applications
1. X-ray Imaging:
• X-ray imaging relies on the Compton
Effect to create detailed images of
internal structures in the human body.
• When X-rays pass through tissues, they
scatter due to interactions with electrons.
The scattered X-rays provide information
about the density and composition of the
tissues.
• Medical X-ray machines use this
phenomenon to visualize bones, organs,
and soft tissues, aiding in diagnosis and
treatment planning.

20. Practical Applications
2. X-ray Diffraction:
• X-ray diffraction is a powerful
technique used to study the atomic and
molecular structure of crystalline
materials.
• When X-rays strike a crystal lattice, they
scatter in specific directions due to the
arrangement of atoms within the
crystal.
• By analyzing the diffraction pattern,
scientists can determine the spacing
between atoms and the crystal’s
symmetry.
• X-ray diffraction is widely used in
materials science, chemistry, and
biology to study crystals, proteins, and
other complex structures.

21. Practical
Applications
3. Security Scanning:
• Compton scattering is employed in airport
security scanners and baggage inspection
systems.
• These scanners use low-energy X-rays to detect
hidden objects or suspicious materials.
• The scattered X-rays provide information about
the density and composition of the scanned
items.

22. Practical
Applications
•4. Particle Physics Research:
• In high-energy physics experiments,
Compton scattering plays a role in
understanding fundamental particles.
• Scientists study the scattering of
electrons and photons to probe the
structure of atomic nuclei and explore
the properties of subatomic particles.

23. 1. Calculate the Compton wavelength of a
proton.
2. Reflect on what you’ve learned and what you
found interesting or challenging about the
lesson.

24. 1. Review and prepare for a short quiz next meeting.
2. Conduct further research on the Compton Effect and its
applications in various fields such as medicine, archaeology, and
engineering.
3. Write a short reflection on what you’ve learned and how you think
the Compton Effect can be used in our daily lives.

26. Send us a message or
visit us
City of Batac, Ilocos Norte,
Philippines
(63) 77-600-0459
op@mmsu.edu.ph
Get in Touch
With Us
facebook.com/MMSUofficial
www.mmsu.edu.ph
Follow us for updates