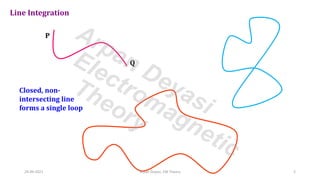
This document discusses vector calculus theorems including Stokes' theorem and the divergence theorem. Stokes' theorem relates the line integral of a vector field around a closed curve to the surface integral of the curl of the vector field over any surface bounded by the curve. The divergence theorem relates the volume integral of the divergence of a vector field over a volume to the surface integral of the vector field over the boundary surface of that volume. The document provides proofs of these theorems and examples of their applications to problems involving conservative vector fields and evaluating integrals.

1. Course: Electromagnetic Theory
paper code: EI 503
Course Coordinator: Arpan Deyasi
Department of Electronics and Communication Engineering
RCC Institute of Information Technology
Kolkata, India
Topics: Vector Integration
29-09-2021 Arpan Deyasi, EM Theory 1
Arpan Deyasi
Electromagnetic
Theory

2. Line Integration
P
Q
Closed, non-
intersecting line
forms a single loop
29-09-2021 Arpan Deyasi, EM Theory 2
Arpan Deyasi
Electromagnetic
Theory

3. Surface Integration
Surface
Closed, non-intersecting line/loop can form an open surface
29-09-2021 Arpan Deyasi, EM Theory 3
Arpan Deyasi
Electromagnetic
Theory

4. Volume Integration
Closed, non-intersecting
surface forms volume
29-09-2021 Arpan Deyasi, EM Theory 4
Arpan Deyasi
Electromagnetic
Theory

5. Line Integration Surface Integration
If 𝑨 is continuous and differentiable at any open surface S formed
by a closed, non-intersecting curve C
( ) ˆ
. .
S
A dr A ndS
= 
 
( )
. .
S
A dr A dS
= 
 
This is Stoke’s theorem
where ෝ
𝒏 is the positive outward normal on the surface S
29-09-2021 Arpan Deyasi, EM Theory 5
Arpan Deyasi
Electromagnetic
Theory

6. Statement of Stoke’s theorem
( )
. .
S
A dr A dS
= 
 
Closed line integration of any continuous and differentiable vector is
numerically equal to the surface integration of curl of that vector where
surface is formed by that non-intersecting closed curve
29-09-2021 Arpan Deyasi, EM Theory 6
Arpan Deyasi
Electromagnetic
Theory

7. Proof of Stoke’s theorem
X
Y
Z
A (x, y) B (x+Δx, y)
C (x+Δx, y+Δy)
D (x, y+Δy)
Open surface formed by the closed path
Closed path ABCDA
𝑷 is continuous and differentiable
at the surface
29-09-2021 Arpan Deyasi, EM Theory 7
Arpan Deyasi
Electromagnetic
Theory

8. Proof of Stoke’s theorem
Value of the vector from A to B  
x
P x
= 
Value of the vector from B to C
y
y
P
P x y
x

 
 
= +  
 
 

 
 
y
y
P
P y x y
x

 
 
 
=  +  
 
 
  
 
 
29-09-2021 Arpan Deyasi, EM Theory 8
Arpan Deyasi
Electromagnetic
Theory

9. Proof of Stoke’s theorem
Value of the vector from C to D
  x
x
P
P x y x
y
 
 

= −  −  
 
 

 
 
x
x
P
P y x
y
 
 

= − +  
 
 

 
 
Value of the vector from C to D
Value of the vector from D to A
y
P y
 
= − 
 
29-09-2021 Arpan Deyasi, EM Theory 9
Arpan Deyasi
Electromagnetic
Theory

10. Proof of Stoke’s theorem
Value of the vector over ABCDA
y x
P P
x y
x y

 
   

= −  
 
   
 
 
 
 
( ) .
z
P dS
= 
( ) y x
z
P P
P
x y

 
   

 = −
 
   
 
 
 
 
29-09-2021 Arpan Deyasi, EM Theory 10
Arpan Deyasi
Electromagnetic
Theory

11. Proof of Stoke’s theorem
X
Y
O
For plane XOY
( )
. .
XOY z
S
P dr P dS
= 
 
For plane YOZ
( )
. .
YOZ x
S
P dr P dS
= 
 
For plane ZOX
( )
. .
ZOX y
S
P dr P dS
= 
 
29-09-2021 Arpan Deyasi, EM Theory 11
Arpan Deyasi
Electromagnetic
Theory

12. Proof of Stoke’s theorem
Combining all the planes
( )
. .
S
P dr P dS
= 
 
29-09-2021 Arpan Deyasi, EM Theory 12
Arpan Deyasi
Electromagnetic
Theory

13. Stoke’s theorem
for every closed curve is that 𝑨 is irrotational
. 0
Adr =

Prob 1: Show that necessary and sufficient condition that
Soln
𝑨 is irrotational ( ) 0
A
 =
( )
. . 0
S
A dr A dS
=  =
 
So the condition is sufficient
29-09-2021 Arpan Deyasi, EM Theory 13
Arpan Deyasi
Electromagnetic
Theory

14. Stoke’s theorem
Let
( ) ˆ
A n

 = β is positive constant
( )
ˆ ˆ
. . 0
S
Adr n n dS

 = 
 
This contradicts the hypothesis
( ) 0
A
 = is the necessary condition also
29-09-2021 Arpan Deyasi, EM Theory 14
Arpan Deyasi
Electromagnetic
Theory

15. Conservative Vector Field
If 𝑷 is irrotational, then the vector field is conservative
0
P
 =
If
Then 𝑷 is conservative vector field
P 
 = 
We know that
0

 =
29-09-2021 Arpan Deyasi, EM Theory 15
Arpan Deyasi
Electromagnetic
Theory

16. Conservative Vector Field
Prob 2: Show that for conservative field, work done is path independent
Soln
Work done
2
1
.
P
P
W F dr
= 
2
1
.
P
P
W dr

= 

( )
2
1
ˆ ˆ
ˆ ˆ ˆ ˆ
. ( )
P
P
W i j k dxi dyj dzk
x y z
  
 
  
= + + + +
 
  
 

29-09-2021 Arpan Deyasi, EM Theory 16
Arpan Deyasi
Electromagnetic
Theory

17. Conservative Vector Field
2
1
P
P
W dx dy dz
x y z
  
 
  
= + +
 
  
 

W d
=
2 1
P P
W  
= −
Therefore, work done depends on the potentials of starting and end points,
but not on the path joining them
29-09-2021 Arpan Deyasi, EM Theory 17
Arpan Deyasi
Electromagnetic
Theory

18. If 𝑨 is continuous and differentiable at any volume V formed by a
closed, non-intersecting surface S
( ) ˆ
. .
V
S
A dV A ndS
 =
 
( )
. .
V
S
A dV A dS
 =
 
where ෝ
𝒏 is the positive outward normal on the surface S
This is Divergence theorem
Volume Integration Surface Integration
29-09-2021 Arpan Deyasi, EM Theory 18
Arpan Deyasi
Electromagnetic
Theory

19. Statement of Divergence theorem
( )
. .
V
S
A dV A dS
 =
 
Volume integration of divergence of any continuous and differentiable
vector over any closed surface is numerically equal to the surface
integration of that vector where volume is formed by the non-intersecting
closed surface
29-09-2021 Arpan Deyasi, EM Theory 19
Arpan Deyasi
Electromagnetic
Theory

20. Proof of Divergence theorem
Z
X
Y
O
A (x, y) B (x+Δx, y)
C (x+Δx,
y+Δy)
Net outward flux while moving From A to B
1
2
x
x
P
P dx dydz
x

 
 
+  
 

 
 
Net outward flux while moving From B to C
1
2
y
y
P
P dy dzdx
y

 
 
+
 
 

 
 
29-09-2021 Arpan Deyasi, EM Theory 20
Arpan Deyasi
Electromagnetic
Theory

21. Proof of Divergence theorem
A (x, y) B (x+Δx, y)
C (x+Δx,
y+Δy)
O
Z
X
Y
Net outward flux while moving From C to D
1
2
x
x
P
P dx dydz
x

 
 
−  
 

 
 
Net outward flux while moving From D to A
1
2
y
y
P
P dy dzdx
y

 
 
−
 
 

 
 
29-09-2021 Arpan Deyasi, EM Theory 21
Arpan Deyasi
Electromagnetic
Theory

22. Proof of Divergence theorem
Net outward flux along X-direction
1
2.
2
x x
P P
dxdydz dxdydz
x x
 
   
=
   
 
   
Net outward flux along Y-direction
1
2.
2
y y
P P
dydzdx dydzdx
y y
 
   
=
   
 
   
Net outward flux along Z-direction
1
2.
2
z z
P P
dzdxdy dzdxdy
z z
 
   
=
   
 
   
29-09-2021 Arpan Deyasi, EM Theory 22
Arpan Deyasi
Electromagnetic
Theory

23. Proof of Divergence theorem
Total outward flux
. y
x z
S
P
P P
P dS dxdydz
x y z

 
 
= + +
 
  
 
 
( )
. .
V
S
P dS P dV
= 
 
29-09-2021 Arpan Deyasi, EM Theory 23
Arpan Deyasi
Electromagnetic
Theory

24. Prob 3: Evaluate
Divergence theorem
( )
. .
V
S
r dS r dV
= 
 
.
S
r dS

Soln
Using Divergence theorem
ˆ ˆ
ˆ ˆ ˆ ˆ
. .( )
V
S
r dS i j k xi yj zk dV
x y z
 
  
= + + + +
 
  
 
 
29-09-2021 Arpan Deyasi, EM Theory 24
Arpan Deyasi
Electromagnetic
Theory

25. Divergence theorem
.
V
S
r dS x y z dV
x y z
 
  
= + +
 
  
 
 
. 3
V
S
r dS dV
=
 
. 3
S
r dS V
=

29-09-2021 Arpan Deyasi, EM Theory 25
Arpan Deyasi
Electromagnetic
Theory

26. Divergence theorem
Prob 4: Show that
( ) ˆ.
V
S
dV n dS
 
 =
 
Soln
Using Divergence theorem
( )
. .
V
S
A dV A dS
 =
 
Let
A B

= 𝑩 is constant
Let
A B

=
29-09-2021 Arpan Deyasi, EM Theory 26
Arpan Deyasi
Electromagnetic
Theory

27. Divergence theorem
( )
. .
V
S
B dV B dS
 
 =
 
( ) ˆ
. .
V
S
B dV B ndS
 
 =
 
( ) ˆ
. ( . )
V
S
B dV B n dS
 
 =
 
29-09-2021 Arpan Deyasi, EM Theory 27
Arpan Deyasi
Electromagnetic
Theory

28. Divergence theorem
( ) ˆ
. . ( )
V
S
B dV B n dS
 
 =
 
( ) ˆ
( )
V
S
dV n dS
 
 =
 
29-09-2021 Arpan Deyasi, EM Theory 28
Arpan Deyasi
Electromagnetic
Theory

29. Divergence theorem
Prob 5: Show that ( ) ˆ
( )
V
S
A dV n A dS
 = 
 
Soln
Using Divergence theorem ( )
. .
V
S
P dV P dS
 =
 
Let
P A B
= 
29-09-2021 Arpan Deyasi, EM Theory 29
Arpan Deyasi
Electromagnetic
Theory

30. Divergence theorem
( )
.[ ] [ ].
V
S
A B dV A B dS
  = 
 
( ) ˆ
. . [ ]
V
S
B A dV B n A dS
 = 
 
( ) ˆ
[ ]
V
S
A dV n A dS
 = 
 
29-09-2021 Arpan Deyasi, EM Theory 30
Arpan Deyasi
Electromagnetic
Theory

31. Green’s theorem
Let
( )
. .
V
S
P dV P dS
 =
 
From Divergence theorem
P  
= 
( )
. .
V
S
dV dS
   
  = 
 
29-09-2021 Arpan Deyasi, EM Theory 31
Arpan Deyasi
Electromagnetic
Theory

32. Green’s theorem
( )
2
. .
V
S
dV dS
     
 +   = 
 
………. (2)
This is Green’s First Identity
Interchanging φ and ψ
( )
2
. .
V
S
dV dS
     
 +   = 
 
………. (1)
29-09-2021 Arpan Deyasi, EM Theory 32
Arpan Deyasi
Electromagnetic
Theory

33. Green’s theorem
This is Green’s Second Identity
Substituting (2) from (1)
( ) ( )
2 2
.
V
S
dV dS
       
 −  =  − 
 
29-09-2021 Arpan Deyasi, EM Theory 33
Arpan Deyasi
Electromagnetic
Theory

34. Helmhotz’s theorem
A vector field can be uniquely defined by its divergence and curl
Proof
We consider two vectors 𝑷 and 𝑸 defined, continuous and differentiable
In a closed, non-intersecting surface S which forms the volume V
ˆ ˆ
. .
P n Q n
=
ˆ
( ). 0
P Q n
− = ………. (1)
29-09-2021 Arpan Deyasi, EM Theory 34
Arpan Deyasi
Electromagnetic
Theory

35. Helmhotz’s theorem
At any arbitrary point
. .
P Q
 = 
.( ) 0
P Q
 − = ………. (2)
Again, at that point
P Q
 = 
( ) 0
P Q
 − = ………. (3)
29-09-2021 Arpan Deyasi, EM Theory 35
Arpan Deyasi
Electromagnetic
Theory

36. Helmhotz’s theorem
Let
( )
R P Q
= −
Since 𝑹 is both solenoidal and irrotational
R 
= 
where φ is arbitrary scalar function
………. (4)
. 0

  =
From (2)
29-09-2021 Arpan Deyasi, EM Theory 36
Arpan Deyasi
Electromagnetic
Theory

37. Helmhotz’s theorem
2
0

 =
Using Green’s First Identity
( )
2
. .
V
S
dV dS
     
 +   = 
 
For φ = ψ
( )
2
. .
V
S
dV dS
     
 +   = 
 
29-09-2021 Arpan Deyasi, EM Theory 37
Arpan Deyasi
Electromagnetic
Theory

38. Helmhotz’s theorem
( )
2
.
V
S
dV dS
  
 = 
 
( )
2
.
V
S
dV R dS
 
 =
 
ˆ
( ). 0
P Q n
− =
From (1)
ˆ
. 0
R ndS =
29-09-2021 Arpan Deyasi, EM Theory 38
Arpan Deyasi
Electromagnetic
Theory

39. Helmhotz’s theorem
ˆ
. 0
R ndS =

( )
2
0
V
dV

  =

0

 =
0
P Q
− =
29-09-2021 Arpan Deyasi, EM Theory 39
Arpan Deyasi
Electromagnetic
Theory

40. Helmhotz’s theorem
P Q
=
Therefore, the vector is unique which can be defined
by its divergence and curl
29-09-2021 Arpan Deyasi, EM Theory 40
Arpan Deyasi
Electromagnetic
Theory