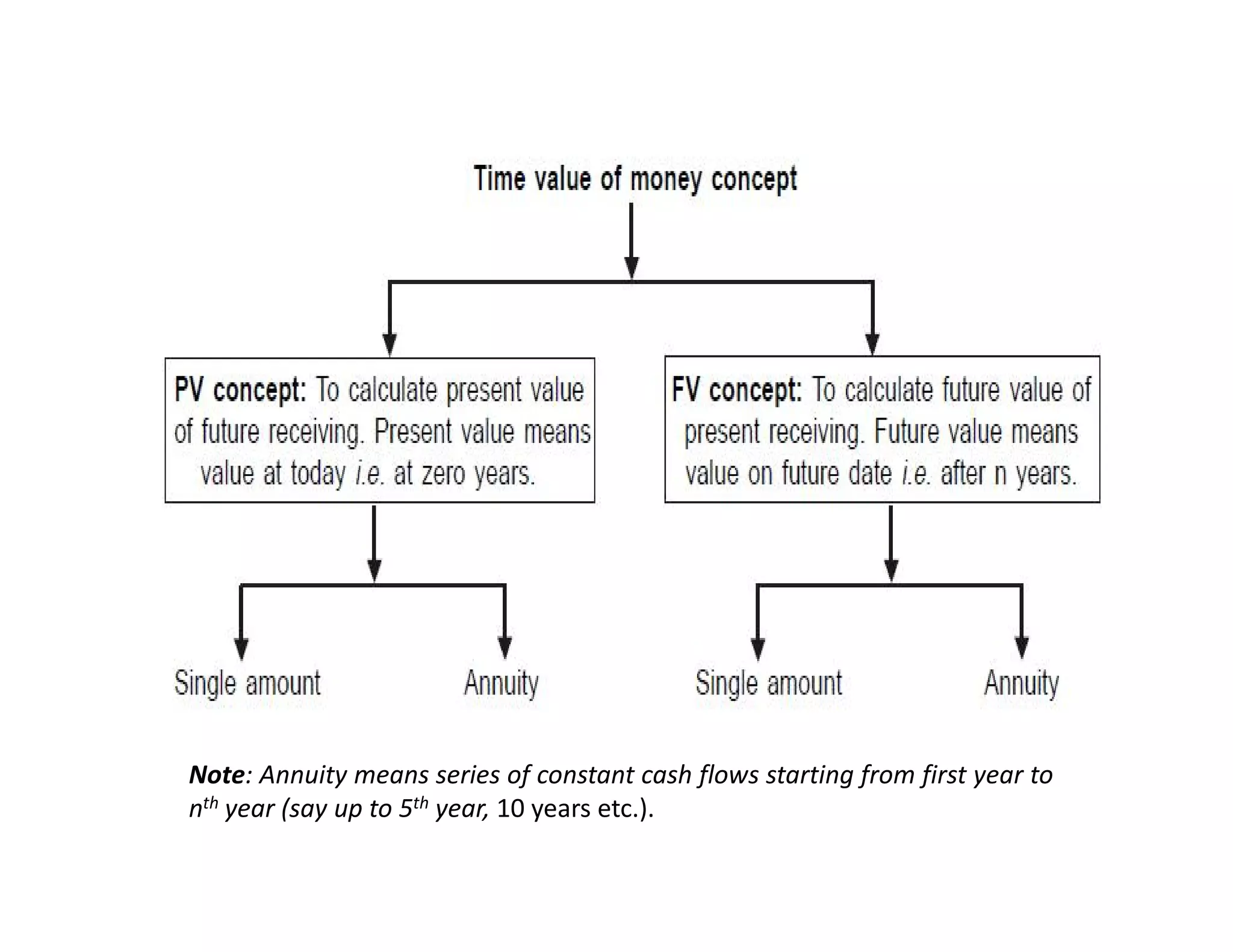
The document explains the concepts of the time value of money, emphasizing that money received today is worth more than the same amount received in the future due to factors like interest rates and compounding. It covers the definitions of present and future values, different types of interest (simple vs. compounding), and formulas for calculating the future and present values of single amounts and annuities. Additionally, it discusses rules for estimating the doubling period of investments and the effects of multiple compounding periods and effective vs. nominal interest rates.

1. Time Value of Money

2. Would you prefer to
have 1 crore now or 1
crore 10 years from
now?
Would you prefer to
have 1 crore now or 1
crore 10 years from
now?

3. The Terminology of Time ValueThe Terminology of Time Value
 Present Value - An amount of money today, or the
current value of a future cash flow
 Future Value - An amount of money at some future
time period
 Period - A length of time (often a year, but can be a
month, week, day, hour, etc.)
 Interest Rate - The compensation paid to a lender (or
saver) for the use of funds expressed as a percentage
for a period (normally expressed as an annual rate)
 Present Value - An amount of money today, or the
current value of a future cash flow
 Future Value - An amount of money at some future
time period
 Period - A length of time (often a year, but can be a
month, week, day, hour, etc.)
 Interest Rate - The compensation paid to a lender (or
saver) for the use of funds expressed as a percentage
for a period (normally expressed as an annual rate)

4. Time Value of Money
• The value of money changes with change in
time.
• A rupee received today is more valuable than
a rupee received one year later.
– Present Value concept (PV concept)
– Future or Compounding Value concept (FV
concept)
• The value of money changes with change in
time.
• A rupee received today is more valuable than
a rupee received one year later.
– Present Value concept (PV concept)
– Future or Compounding Value concept (FV
concept)

5. Reasons for Time Preference of Money
• Uncertain future
• Risk involvement
• Present needs
• Return
• Uncertain future
• Risk involvement
• Present needs
• Return

6. Note: Annuity means series of constant cash flows starting from first year to
nth year (say up to 5th year, 10 years etc.).

7. Future Value of a Single Amount
Say that you put $1,000 into the bank
today. How much will you have after a
year? After two years? This kind of
problem is called a future value /
compounding problem.
Say that you put $1,000 into the bank
today. How much will you have after a
year? After two years? This kind of
problem is called a future value /
compounding problem.

8. Compounding vs. Simple Interest
• Compounding interest is defined as earning
interest on interest.
• Simple interest is interest earned on the
principal investment.
• Principal refers to the original amount of
money invested or saved
• Compounding interest is defined as earning
interest on interest.
• Simple interest is interest earned on the
principal investment.
• Principal refers to the original amount of
money invested or saved

9. Future Value of a Single Amount
You have Rs.1,000 today and you deposit it
with a financial institution, which pays 10
per cent interest compounded annually,
for a period of 3 years. What is the total
amount after 3 years?
You have Rs.1,000 today and you deposit it
with a financial institution, which pays 10
per cent interest compounded annually,
for a period of 3 years. What is the total
amount after 3 years?

10. Formula
FVn =PV×(1+k)n
FVn = Future value n years
PV = Present Value (cash today)
k = Interest rate per annum
n = Number of years for which compounding
is done
FVn =PV×(1+k)n
FVn = Future value n years
PV = Present Value (cash today)
k = Interest rate per annum
n = Number of years for which compounding
is done

11. If you deposit Rs.10,000 today in a bank
which pays 12% interest compounded
annually, how much will the deposit
grow to after 10 years and 12 years?
Example
If you deposit Rs.10,000 today in a bank
which pays 12% interest compounded
annually, how much will the deposit
grow to after 10 years and 12 years?

12. Doubling period
• How much time is required to double my
investment?
• The length of period which an amount is going
to take o double at a certain given rate of
interest.
• How much time is required to double my
investment?
• The length of period which an amount is going
to take o double at a certain given rate of
interest.

13. Rule of 72
72
Doubling Period = ---------------------
Rate of Interest
72
Doubling Period = ---------------------
Rate of Interest

14. If you deposit Rs.10,000 today at 6 per
cent rate of interest, in how many
years will this amount double?
Workout this with the rule of 72.
Example
If you deposit Rs.10,000 today at 6 per
cent rate of interest, in how many
years will this amount double?
Workout this with the rule of 72.

15. Rule of 69
69
Doubling Period = 0.35 + ---------------------
Rate of Interest
69
Doubling Period = 0.35 + ---------------------
Rate of Interest

16. If you deposit Rs.20,000 today at 6 per
cent rate of interest, in how many
years will this amount double?
Workout this with the rule of 69.
Example
If you deposit Rs.20,000 today at 6 per
cent rate of interest, in how many
years will this amount double?
Workout this with the rule of 69.

17. Multiple Compounding Periods
• Interest may have to be compounded more
than once a year.
• Example: Banks may allow interest on
quarterly or half yearly basis; or a company
may allow compounding of interest twice a
year.
• Interest may have to be compounded more
than once a year.
• Example: Banks may allow interest on
quarterly or half yearly basis; or a company
may allow compounding of interest twice a
year.

18. Formula
FVn =PV×(1+k/m)m x n
FVn = Future value n years
PV = Present Value (cash today)
k = Interest rate per annum
n = Number of years for which compounding
is done
m = Number of times compounding is done
during a year
FVn =PV×(1+k/m)m x n
FVn = Future value n years
PV = Present Value (cash today)
k = Interest rate per annum
n = Number of years for which compounding
is done
m = Number of times compounding is done
during a year

19. Calculate the compound vale of
Rs.10,000 at the end of 3 years at 12%
rate of interest when interest is
calculated on
– Yearly basis
– Half yearly basis
– Quarterly basis
Example
Calculate the compound vale of
Rs.10,000 at the end of 3 years at 12%
rate of interest when interest is
calculated on
– Yearly basis
– Half yearly basis
– Quarterly basis

20. Effective Vs. Nominal Rate
• Effective Interest rate: The percentage
rate of return on an annual basis. It
reflects the effect of intra-year
compounding. (Ex. 12.36%)
• Nominal Interest rate: Interest rate
expresses in monitory terms. (Ex. 12%)
• Effective Interest rate: The percentage
rate of return on an annual basis. It
reflects the effect of intra-year
compounding. (Ex. 12.36%)
• Nominal Interest rate: Interest rate
expresses in monitory terms. (Ex. 12%)

21. Formula
ERI = (1 + k/m)m – 1
ERI = Effective Rate of Interest
k = Nominal Rate of Interest
m = Frequency of compounding per year
ERI = (1 + k/m)m – 1
ERI = Effective Rate of Interest
k = Nominal Rate of Interest
m = Frequency of compounding per year

22. Example
A bank offers 8 per cent nominal rate of
interest on deposits. What is the effective
rate of interest if the compounding is done
i) half yearly
ii) quarterly &
iii) monthly
A bank offers 8 per cent nominal rate of
interest on deposits. What is the effective
rate of interest if the compounding is done
i) half yearly
ii) quarterly &
iii) monthly

23. Future Value of an Annuity
• Suppose you deposit Rs.1,000 annually in a
bank for 5 years and your deposits earn a
compound interest rate of 10 per cent. What
will be the value of this series of deposits (an
annuity) at the end of 5 years?
• Suppose you deposit Rs.1,000 annually in a
bank for 5 years and your deposits earn a
compound interest rate of 10 per cent. What
will be the value of this series of deposits (an
annuity) at the end of 5 years?

24. • 1000 (1.1)4 + 1000 (1.1)3 + 1000 (1.1)2 +
1000 (1.1)1 + 1000
• 1000 (1.4641) + 1000 (1.331) + 1000 (1.21) +
1000 (1.1) + 1000
• 6,105
• 1000 (1.1)4 + 1000 (1.1)3 + 1000 (1.1)2 +
1000 (1.1)1 + 1000
• 1000 (1.4641) + 1000 (1.331) + 1000 (1.21) +
1000 (1.1) + 1000
• 6,105

25. Formula
(1 + K)n – 1
FVAn = A -----------
K
FVAn = Future value of an Annuity n years
A = Constant periodic flow
k = Interest rate per period
n = duration of the annuity
(1 + K)n – 1
FVAn = A -----------
K
FVAn = Future value of an Annuity n years
A = Constant periodic flow
k = Interest rate per period
n = duration of the annuity

26. (1 +.1)5 – 1
• FVA = 1000 --------------------
.1
(1 +.1)5 – 1
• FVA = 1000 --------------------
.1

27. Present Value of a Single Amount
• Suppose someone promises to give you
Rs.1,000 three years hence. What is the
present value of this amount if the interest
rate is 10 per cent?
• Suppose someone promises to give you
Rs.1,000 three years hence. What is the
present value of this amount if the interest
rate is 10 per cent?

28. Formula
n
PV = FVn

29. Present Value of An Annuity
Suppose you expect to receive Rs.1,000
annually for 3 years, each receipt occurring at
the end of the year. What is the present value
of this stream of benefits I the discount rate is
10 per cent?
Suppose you expect to receive Rs.1,000
annually for 3 years, each receipt occurring at
the end of the year. What is the present value
of this stream of benefits I the discount rate is
10 per cent?

30. • 1000 (1/1.1) + 1000 (1/1.1)2 + 1000 (1/1.1)3
• 1000x.909 + 1000x.826 + 1000x.751
• 2486
• 1000 (1/1.1) + 1000 (1/1.1)2 + 1000 (1/1.1)3
• 1000x.909 + 1000x.826 + 1000x.751
• 2486